Maths
- 2 -
Perspectives
© The scientific sentence. 2010
|
Mathématiques 2: Geométrie: Les Perspectives:
Exercises résolus
Exercises résolus
1. Les prismes:
Un prisme est polyèdre ayant deux faces
isométriques et parallèles appelées bases.
Les parallélogrammes qui relient ces deux bases sont
appelés faces latérales.
Un prisme est droit si ses faces latérales sont de
rectangles.
Un prisme est régulier s'il est droit est que la base
est un polygone régulier.
Exemple:
a) Prisme régulier à base triangulire:
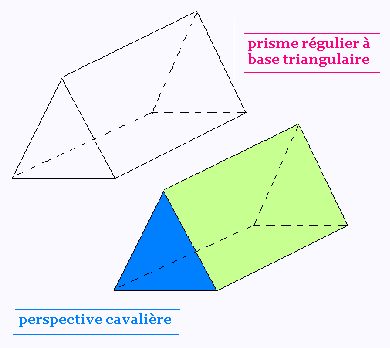
b) Prisme droit à base pentagonale:
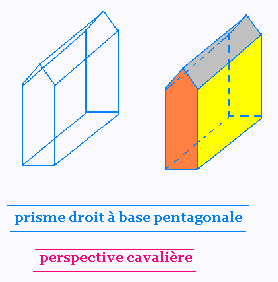
c) prisme régulier à base carrée:
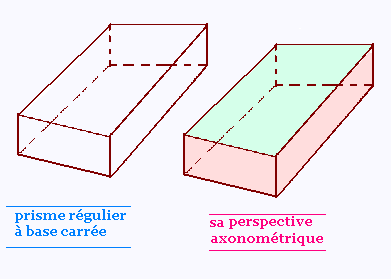
2. Les tours
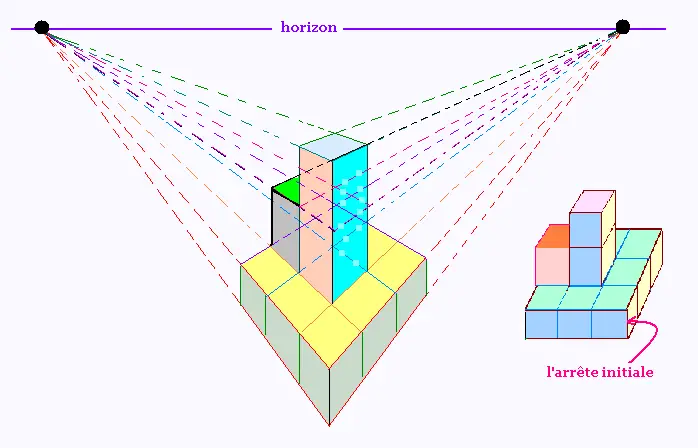
2.1. Tour 1
Toutes les quatre faces latérales sont identiques.
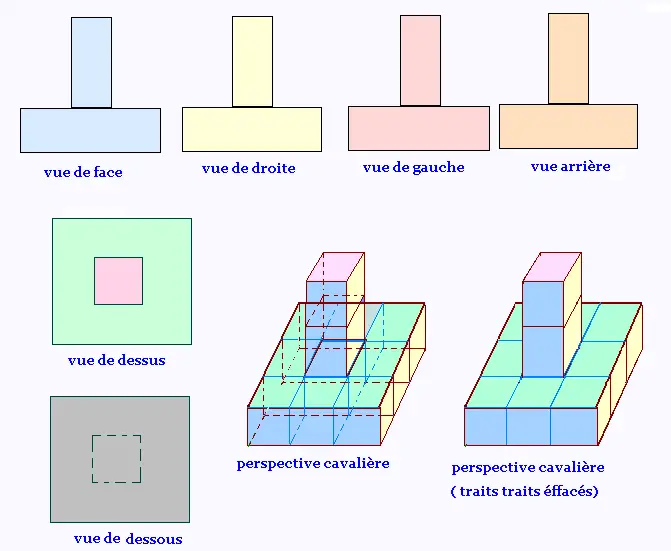
Projection centrale à deux points de fuites de cette tour.
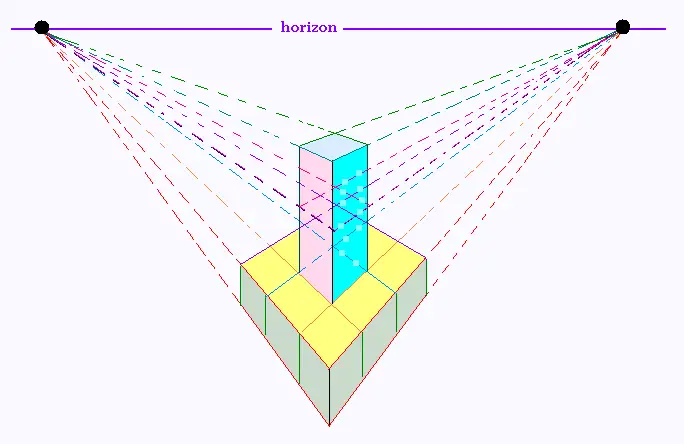
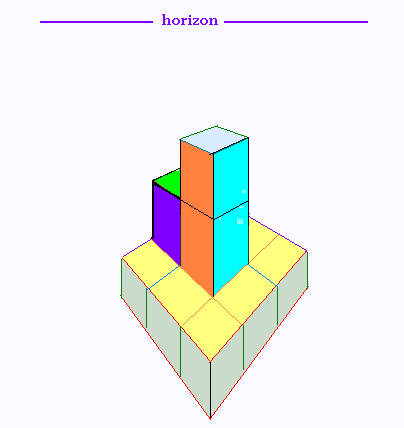
Projection centrale à deux points de fuites de cette tour,
avec suppression des fuyantes
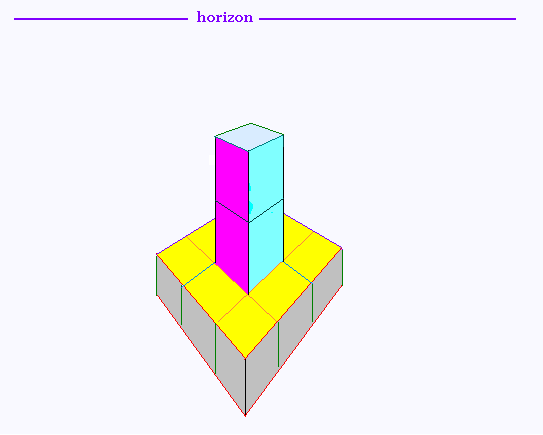
2.2. Tour 2
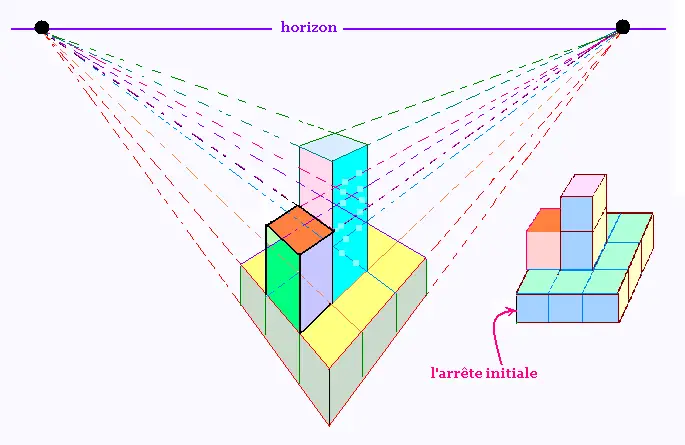

3. L'escalier:
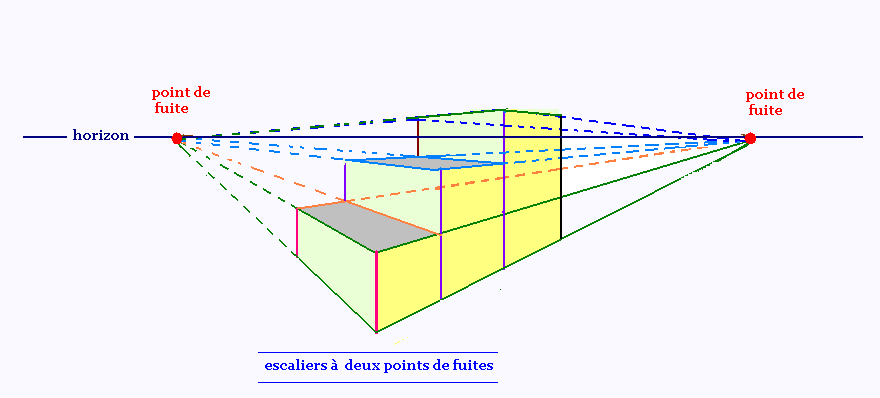
Projection centrale à deux points de fuites
d'un esclaier à 3 marches
1. Proche de l'horizon: C'est l'exercice 9
Après l'horizon, on ne voit plus les marches, mais
les contre-marches restent visibles.
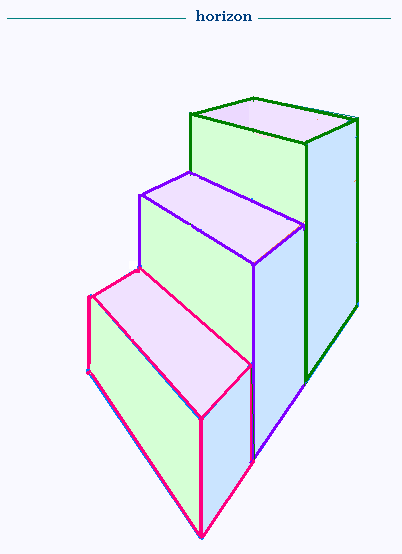
En effaçant les fuyantes :
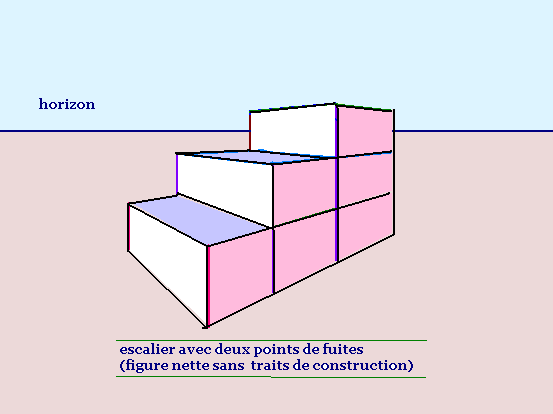
2. Loin de l'horizon
On voit les marches et les contre-marches.
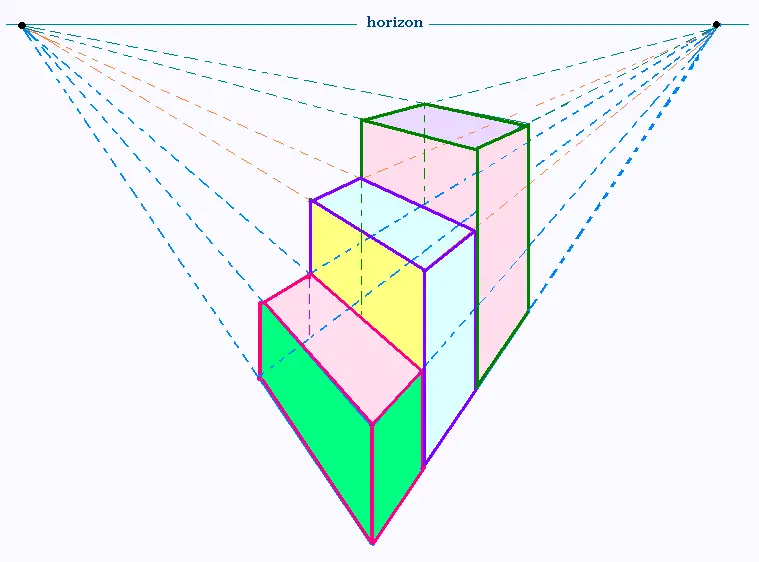
En effaçant les fuyantes :
4. Rappels: Les projections et les perspectives
1. Projection:
La projection est la représentation d'un objet en 3 dimensions
sur un plan.
C'est une opération qui transforme les points et donc les
lignes d'un objet en d'autres points et lignes en traçant des droites
parallèles appelées projetantes.
Ces projections sont dites orthogonales si les
projetantes sont perpendiculaires au plan de projection.
Il esiste 3 types de projections:
Les projections sont parallèles ou centrales, ou orthogonales.
La projection parallèle contient la perspective
cavalière et la perspective axonométrique (ou isométrique).
La projection centrale contient la perspective à un point
de fuite et la perspective à deux points de fuite.
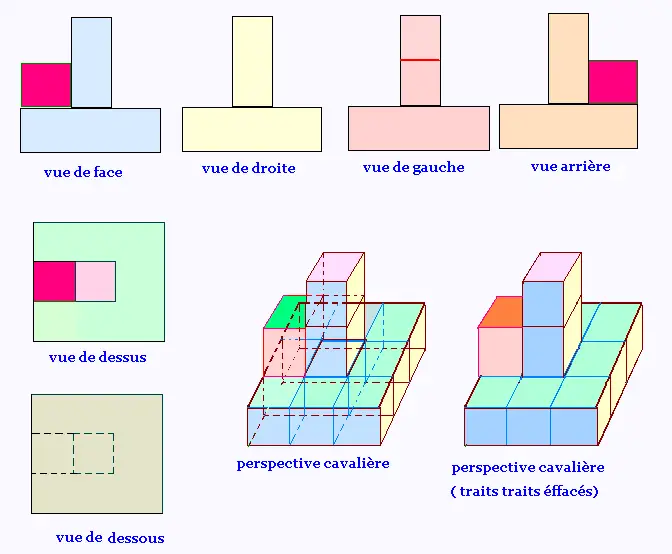
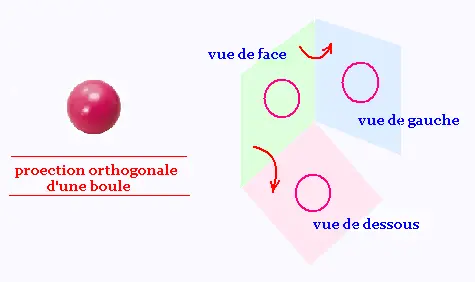
La projection orthogonale contient la vue de face ou arrière,
vue de gauche ou de droite, vue de dessus ou de dessous.
Trois vues suffisent en général pour définir un objet.
2. Perspectives
Dans la perspecticve cavalière, on commence par dessiner
une FACE frontale et on respecte le parallélisme.
L'angle de fuite est 45°.
Dans la perspective axonométrique (isométrique), on commence
par dessiner une ARÊTE et on respecte le parallélisme .
L'angle de fuite est 30°.
Dans la perspecticve centrale (ou conique) à
un point de fuite, on commence par dessiner une FACE frontale
et on respecte l'éloignement (ou ligne d'horizon).
Dans la perspective à deux points de fuite, on commence par
dessiner une ARÊTE et on respecte l'éloignement.
On retient:
• Parallèle: cavalière - face - 45o.
• Parallèle: axonométrique - arrête - 30o.
• Centrale: À 1 point de fuite - face.
• Centrale: À 2 points de fuite - arrête.
• Orthogonale : 3 faces.
5. Construction d'un solide
à partir de ses projections orthogonales
Solide 1:
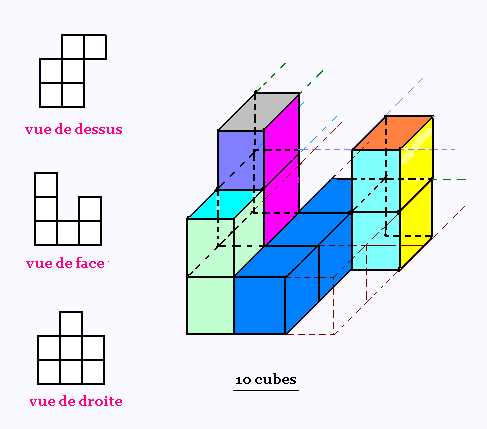
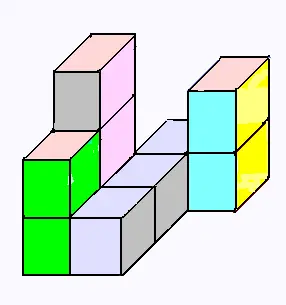
Solide 2:
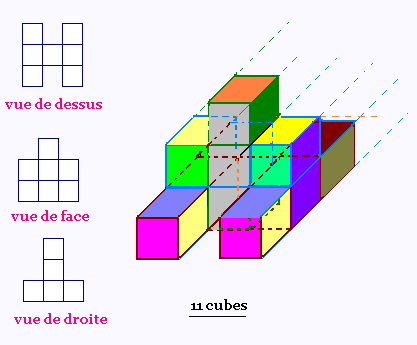
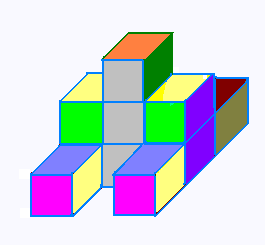
6. Vue dans l'espace:
empilements des cubes identiques
avec perspective cavalière
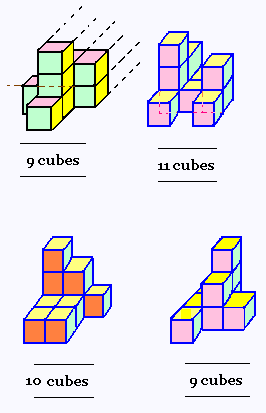
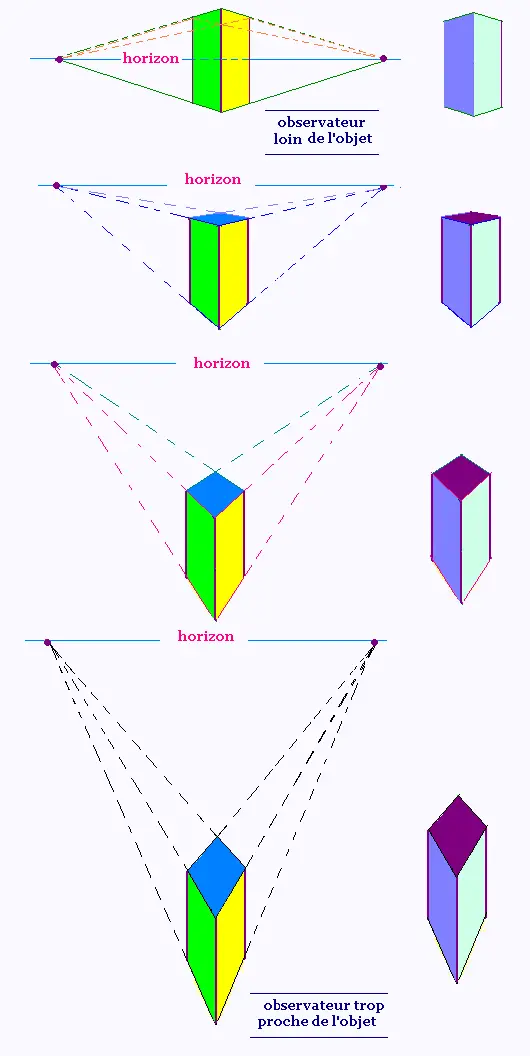
7. Vue d'un cube en :
perspective à deux points de fuite
selon la position de l'observateur
|
|