Mathématiques 2: Probabilités
L'expérience aléatoire à plusieurs étapes
avec et sans remise

1. L'arbre des probabilités

L'arbre des probabilités est très utile pour dénombrer les résultats possibles d'une expérience aléatoire à plusieurs étapes.

Dans un sac il y a 9 billes au total. 4 billes jaunes, 3 billes blues, et 2 billes rouges.

On considère l'expérience aléatoire suivante:

On tire une première bille du sac, on marque sa couleur, et on la remet dans le sac; puis on tire une deuxième bille et on marque sa couleur.

on considère l'évenement élémentaire suivant:

Tirer une bille blue suivie d'une bille rouge.

Cet événement est élémentaire et l'expérience aléatoire est à plusieurs étapes, à deux étapes.

Pour dénombrer les résultats possibles d'une expérience aléatoire à plusieurs étapes, il est utile d'utiliser le diagramme en arbre.

Sur chacune des branches de l'arbre, on ecrit une probabilité; on obtient un arbre des probabilités.

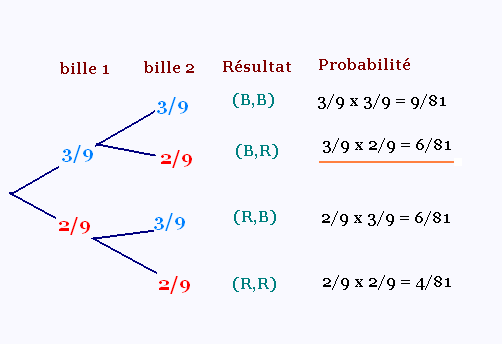
On peut mener une expérience aléatoire à plusieurs étapes avec remise ou sans remise. Avec remise, les probabilités des événements intermédiaires demeurent identiques d'étape en étape. Sans remise, le résultat d'une étape influence les probabilités de l'étape suivante.

2. L'expérience aléatoire à plusieurs étapes
avec remise

Dans l'expérience plus haut, après chaque tirage, la bille été remise dans le sac pour tirer de nouveau une bille. C'est une expérience aléatoire avec remise.

3. L'expérience aléatoire à plusieurs étapes
sans remise

L'expérience sans remise consiste à ne pas remettre la bille après chaque tirage. À chaque étape de l'expérience, le nombre de billes dans le sac diminue d'une unité.

Pour l'expérience aléatoire à deux étapes sans remise, l'arbre des probabilités est le suivant:

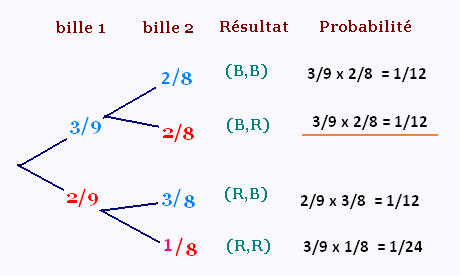
4. Dépendance des événements

Deux événements sont indépendants si la réalisation de l'un n'influence pas la probabilité de réalisation de l'autre.

Je joue au pile ou face avec une pièce de monnaie. Je lance la pièce à deux reprises. Le résultat obtenu lors du premier lancer n'influe pas les résultats possibles lors du deuxième lancer.

Deux événements sont dépendants si la réalisation de l'un influence la probabilité de réalisation de l'autre.

On tire successivement et sans remise deux billes d'un sac. Le résultat obtenu lors du premier tirage influence les résultats possibles lors du deuxième tirage.

5. Exemples

5.1. Exemple 1

Dans une bibliothèque, nous avons 5 livres de Chimie (C), 7 Livres de Physique (P) et 13 livres de Mathématiques (M).

Ces livres sont placés de manière indiscernable sur des étagères.

L'expérience aléatoire consiste à prendre 2 livres parmis les 25 livres de la bibliothèque.

Cette expérience est une expérience aléatoire puisqu'on ne peut pas prévoir le résultat de façon certaine.

Cette expérience est une expérience sans répétition puisqu'il n'y a pas de remise.

Cette expérience est une expérience à plusieurs étapes (2 étapes) puisqu'on tire un objet puis on tire un autre une deuxième fois d'un lot d'objets qui sont des livres.

Il faut donc utiliser un diagramme en arbre et multiplier les probabilités.

Voici ce diagramme en arbe:

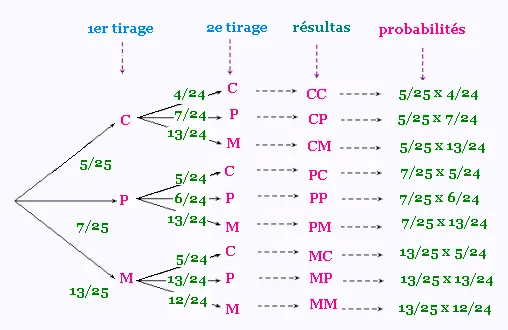
5.2. Exemple 2

On veut distribuer 4 livres aux élèves d'une classe qui contient 5 filles et 12 garçons. On fait un tirage au sort.

a) Quelle est la probabilité que les deux premiers soient des filles suivi d' d'un garçon et puis ensuite d'une fille:

b) Est-ce que toutes les chances d'avoir gagné un livre sont les mêmes pour tout le monde?

Cette expérience est aléatoire, sans remise et à plusieurs étapes (4 étapes).

Ce problème peut se reformuler comme suit:

Je tire 4 billes d'une boîte qui en contient 17. 5 grises et 12 jaunes. Le tirage est une à la fois et est sans remise.

a) La probabilité de tirer 2 grises suivi d' une jaune et puis ensuite d'une grise est:

P = 5/17 x 4/16 x 12/15 x 3/14

b) La probabilité d'être sorti n'est pas la même pour les deux types de billes, parce que leur nombre de départ dans la boîte n'est pas le même. Les événements tirer une bille ne sont pas équiprobables.

3. Exercices

Une boîte contient 11 billes au total; 4 billes jaunes (I), 3 bleus (B), 2 rouges (R) et deux dont on connait pas la couleur et marquées "x".

Determiner la couleur des deux billes marquées "x" si:

a) Sans remise, on a: P(x, R) = 12/110

b) Avec remise, on a: P(B, x) = 18/121

c) Sans remise, on a: P(J, x) = 20/110

d) Sans remise, on a: P(J, x) = 30/110

e) Sans remise, on a: P(J, x) = 80/110