Maths
- 2 -
Probabilités
Probabilités
conditionnelles
Procédures
de votes
© The scientific sentence. 2010
| | |
Mathématiques 2: Ordre et probabilités
On peut réaliser une experience aléatoire de
différentes manières:
Sans remise et sans ordre,
Sans remise avec ordre,
Avec remise et sans ordre, ou
Avec remise et avec ordre.
1. Expérience 1

On réalise une experience aléatoire de tirer
2 livres parmis les 3 livres numérotés
qui sont dans un tas.
- Premièrement sans remise et sans ordre,
- Deuxièment sans remise mais avec ordre,
- Troisièmemnt avec remise et sans ordre, et
- Quatrièment avec remise et avec ordre.
1.1. Au hasard sans ordre
et sans remise
On réalise l'expérience aléatoire suivante
sur un ensemble de 3 livres numérotés
1, 2, 3.
On prend 2 livres au hasard sans ordre
et sans remise
Un résultat possible est R1 = {1,2}
Un autre résultat possible est R2 = {3,2} .
Comme c'est sans ordre, c'est aussi {2,3}.
On a l'arbre suivant:
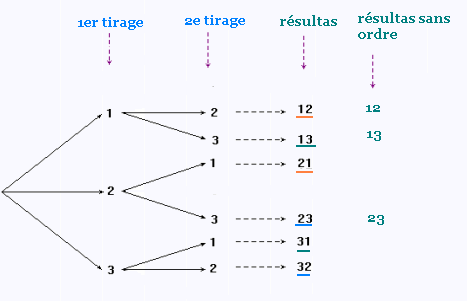
En tout , on a 3 résultats
possibles de prendre 2 livres parmis
les 3 en ne tenant pas compte de l'ordre possibilités, ni de
répétition (remise).
Dans le cas general, Le nombre de
résultats possibles d’une expérience aléatoire
sans ordre et sans remise est égal au:
Nombre de résultats possibles en tenant compte de
l'ordre divisé par le nombre de façons différentes
d'écrire un résultat en tenant compte de l'ordre.
1.2. Au hasard avec ordre
et sans remise
On prend 2 livres au hasard avec ordre
et sans remise . Dans ce cas nous avons
l'arbre des probabilités suivant:
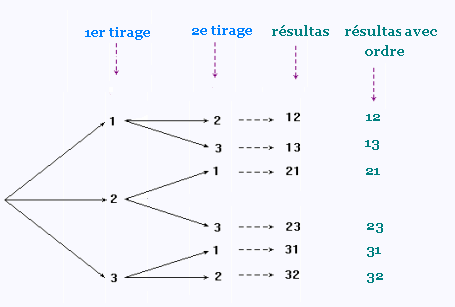
Nous avons donc 6 results possibles.
On peut ecrire chaque résultat de 2 façons
différentes en tenant compte de l'ordre
Ainsi:
Nombre de résultats possibles en tenant compte de
l'ordre = 6
Nombre de façons différentes
d'écrire un résultat en tenant compte de l'ordre = 2
Donc
Le nombre de
résultats possibles sans ordre et sans remise est égal
à 6/2 = 3 . C'est ce qui été trouvé.
1.3. Avec remise et sans ordre
On prend 2 livres au hasard sans ordre
et avec remise . Dans ce cas nous avons
l'arbre des probabilités suivant:
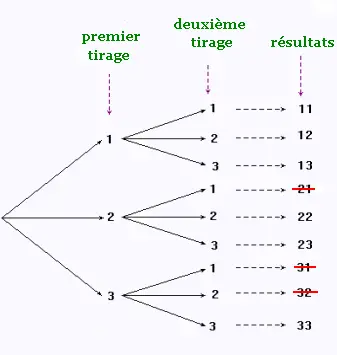
1.4. Avec remise et avec ordre
On prend 2 livres au hasard sans ordre
et sans remise . Dans ce cas nous avons
l'arbre des probabilités suivant:
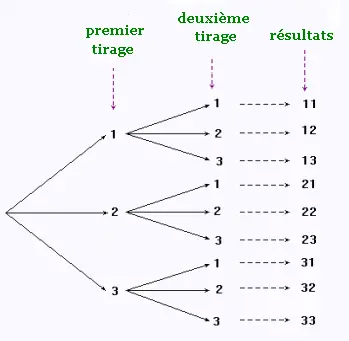
2. Expérience 2
On réalise l'éxpérience aléatoire suivante:
tirer 3 billes de couleur d’un sac contenant
4 billes:
1 rouge, 1 verte, 1 marron et 1 argent.
Sans remise et sans ordre:
Nombre de résultats possibles avec ordre = 24.
Nombre de façons différentes d'écrire un résultat
avec ordre = 6
Donc le nombre de résultats possibles
sans ordre et sans remise est égal à:
24/6 = 4
L’ensemble des résultats possibles de cette
expérience aléatoire (sans ordre et sans remise)
est:
Ω = {(rouge, verte, marron), (rouge, verte, argent),
(rouge, marron, argent), (verte, marron, argent )}.
Voici toutes les possibilités: n = 4 et p = 3
1. Avec remise et avec ordre:
Nous avons tous les cas possibles. Ils sont en nombre de
np = 43 = 64.
2. Sans ordre et sans remise:
Nous avons des cas possibles. Ils sont en nombre de
nombre d'arragements sans ordre = A(p,n)/p! = n!/p!(n - p)!
= 4!/3!(4 - 3)! = 4! = 4.
Ce sont:
(r, v, m), (m, r, a), (v, r, a) et (a, v, m).
3. Sans remise mais avec ordre:
Nous avons des cas possibles. Ils sont en nombre de
nombre d'arragements avec ordre = A(p,n) = n!/(n - p)!
= 4!/(4 - 3)! = 24.
Ce sont :
(r, m, v), (r, m, a), (r, v, m), (r, v, a),
(r, a, m), (r, a, v), (m, r ,v), (m, r, a),
(m, v, r), (m, v, a), (m, a, r), (m, a, v),
(v, r, m), (v,r, a ), (v, m, r), (v, m,a ),
(v,a , r), (v, a, m), (a, r, m), (a, r, v),
(a, m, r), (a, m, v), (a, v, r), (a, v, m).
4. Avec remise et sans ordre:
Nous avons des cas possibles. Ils sont en nombre de
nombre de combinaisons de avec remise
D(p,n) = C(p, n + p - 1) = (n + p - 1)!/p!(n - 1)!
= D(3,4) = C(3, 4 + 3 - 1) = (4 + 3 - 1)!/3!(4 - 1)! =
6!/3!3! = 4 x 5 x 6/6 = 20
3. Exercices
3.1. Exercice 1

Nous avons trois briques de masses différentes
à déplacer.
Quel est le nombre de façons de transporter au moins
2 briques l'une au dessus de l'autre avec ordre ?
3.2. Exercice 2
Combien existe-t-il de nombres entre 10 et 100 000
commençant par un chiffre pair et contenant des
chiffres différents ?
3.3. Exercice 3

Combien peut-on former de nombres de cinq chiffres
différents si ces nombres doivent commencer par 1 ou
3 ou 5, ne pas contenir de zéros et ne pas se terminer
par un 7 ou un 9?
Solutions
|
|