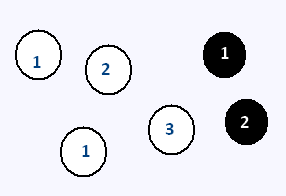
Réponse 1. Il y a quatre boules blanches parmi les six au total, donc la probabilité de tirer une boule blanche est . Réponse A 2. Il y a deux boules portant le numéro 2 parmi les six au total, donc la probabilité de tirer une boule portant le numéro 2 est . Réponse C 3. Il y a deux boules blanches numérotées 1 parmi les six au total, donc la probabilité de tirer une boule blanche numérotée 1 est . Réponse A 4. DNB - Polynésie Française - Juin 2009
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Notes | 2 | 4 | ... | |
| Effectifs | 1 | 3 | ... |
2. Quel est l'effectif total de ce groupe ?
3. Quelle est la moyenne des notes de cette classe ? Arrondir le résultat à 0,1 près.
4. Donner la médiane de ces notes.
5. On choisit au hasard une copie. Quelle est la probabilité pour que la note de cette copie soit supérieure ou égale à 10 ?
Réponse
1.
| Notes | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 15 | 17 | 18 | 19 |
| Effectifs | 1 | 3 | 1 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 4 | 2 | 1 | 2 | 1 |
2. L'effectif total de ce groupe est 1 + 3 + 1 + 2 + 2 + 2 + 2 + 1 + 2 + 2 + 4 + 2 + 1 + 2 + 1 = 28.
3. La moyenne des notes de cette classe est:
(2 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 15 + 17 + 18 + 19 )/28 = 289/28 = 10.3.
4. La médiane des notes:
1 + 3 + 1 + 2 + 2 + 2 + 2 + 1 = 14 = 50% de l'effectif total, qui correspond au 8e rang des caractères; c'est à dire 10.
5. On choisit au hasard une copie. La probabilité pour que la note de cette copie soit supérieure ou égale à 10 est:
(1 + 2 + 2 + 4 + 2 + 1 + 2 + 1 )/28 = 15/28 (plus que 50% de chance de tomber sur une telle copie).
7. DNB - Nouvelle Calédonie - Décembre 2009
Exercice 2
Énoncé
La roussette rousse est une espèce de chauve souris, endémique (indigène)
au territoire de la Nouvelle-Calédonie. Elle sera la mascotte (symbole) officielle
des XIVèmes Jeux du Pacifique
de 2011.
Dans une urne, on a dix boules indiscernables au toucher portant les lettres
du mot ROUSSETTES.

On tire au hasard une boule dans cette urne et on regarde la lettre
inscrite sur la boule.
1. Quels sont les six résultats possibles à l'issue d'un tirage ?
2. Déterminer les probabilités suivantes :
a) la lettre tirée est un R.
b) la lettre tirée est un S.
c) la lettre tirée n'est pas un S.
3. Julie affirme qu'elle a plus de chance d'obtenir une voyelle
qu'une consonne à l'issue d'un tirage.
A-t-elle raison ? Justifier votre réponse.
Réponse
1. Les six résultats possibles à l'issue d'un tirage sont:
{R, O, U, S, E, T}.
a) la probabilité de tirer la lettre R est p(R) = .
b) la probabilité de tirer une lettre S est p(S) = .
c) la probabilité de tirer une lettre autre que S est
p() = .
2.
• la probabilité d'obtenir une voyelle est p(V) = .
• la probabilité d'obtenir une consonne est p(C) = .
Comme . On a plus de chance de tomber
sur une consonne. Julie n'a pas raison.
8. DNB - Pondichéry - Avril 2010
Exercice 1
Énoncé
Une classe de 3ème est constituée de 25 élèves.
Certains sont externes, les autres sont demi-pensionnaires.
Le tableau ci-dessous donne la composition de la classe.
| Garçon | Fille | Total | |
| Externe | ... | 3 | ... |
| Demi-pensionnaire | 9 | 11 | ... |
| Total | ... | ... | 25 |
1. Recopier et compléter le tableau.
2. On choisit au hasard un élève de cette classe.
a) Quelle est la probabilité pour que cet élève soit une fille ?
b) Quelle est la probabilité pour que cet élève soit externe ?
c) Si cet élève est demi-pensionnaire, quelle est la probabilité que ce soit un garçon ?
Réponse
1.
| Garçon | Fille | Total | |
| Externe | 2 | 3 | 5 |
| Demi-pensionnaire | 9 | 11 | 20 |
| Total | 11 | 14 | 25 |
2. On choisit au hasard un élève de cette classe.
a) La probabilité pour que cet élève soit une fille est
p(F) = .
b) La probabilité pour que cet élève soit externe est
p(E) = .
c) La probabilité pour que cet élève soit un garçon, sachant qu'il est demi- pensionnaire est
p(G/DP) = .
9. DNB - Polynésie Française - Juin 2010
Exercice 2
Énoncé
Sur le manège "Caroussel", il y a quatre chevaux, deux ânes, un coq,
deux lions et une vache.
Sur chaque animal, il y a une place. Vaite s’assoit-au hasard sur le manège.
1. Quelle est la probabilité qu’elle monte sur un cheval ? Exprimer le résultat sous
forme d’une fraction irréductible.
2. On considère les évènements suivants :
A : "Vaite monte sur un âne."
C : "Vaite monte sur un coq."
L : "Vaite monte sur un lion."
a. Définir par une phrase l’évènement non L puis calculer sa probabilité.
b. Quelle est la probabilité de l’évènement A ou C.
Exercice 3
Énoncé
Hiti et Kalu sont deux entreprises de cent personnes qui ont
fait paraître les informations suivantes :
| Salaire moyen en francs | Entreprise Hiti | Entreprise Kalu |
| Hommes | 168 000 | 180 000 |
| Femmes | 120 000 | 132 000 |
| Effectif Hommes/ Femmes | Entreprise Hiti | Entreprise Kalu |
| Hommes | 50 | 20 |
| Femmes | 50 | 80 |
Kévin dit à sa sœur: "En moyenne, on est mieux payé chez Kalu." Qu'en pensez-vous ?
L'évaluation de cet exercice tiendra compte des observations et étapes de recherche, même incomplètes ; les faire apparaître sur la copie.
Réponses
Exercice 2
En tout, nous avons 10 animaux.
Vaite s'assoit au hasard sur le manège du caroussel.
1. P(Vaite monte sur un cheval) =
2. a. L'événement L est "Vaite monte sur un lion".
L'événement non L (noté ) est "Vaite ne monte pas sur un lion". C'est l'événement complémentaire (ou contraire) de l'événement L.
La probabilité de cet événement est égal à 1 - P(Vaite monte sur un lion) =
b. Vaite ne peut pas monter à la fois sur deux mêmes animaux en même temps. Ainsi les événements A et C sont incompatibles.
Par conséquent, la probabilité de l'événement A ou C =
P(A ou C) = P(A) + P(C) = P(âne) + P(coq) =
Exercice 3
Il s'agit de calculer les moyennes pondérées des salaires dans chacune des deux entreprises et comparer.
La moyenne des salaires dans l'entreprise Hiti est:
Mh = (50 x 168000 + 50 x 120000)/100 = (168 + 120) x 1000/2 = 288000/2 = 144000 francs.
La moyenne des salaires dans l'entreprise Kalu est:
Mk = (20 x 180000 + 80 x 132000)/100 = (2 x 180 + 8 x 132) x 100 = 141600 francs.
Nous avons: Mk < Mh. Ainsi, on est donc mieux payé dans l'entreprise Hiti. Kévin avait tort.
10. DNB - Liban - Juin 2010
Exercice 2
Énoncé
Un sac contient
10 boules rouges,
6 boules noires et
4 boules jaunes.
Chacune de ces boules a la même probabilité d'être tirée.
On tire une boule au hasard.
1. Calculer la probabilité pour que cette boule soit rouge.
2. Calculer la probabilité pour que cette boule soit noire ou jaune.
3. Calculer la somme des deux probabilités trouvées aux deux
questions précédentes.
Le résultat était-il prévisible ? Pourquoi ?
4. On ajoute dans ce sac des boules bleues. Le sac contient alors
10 boules rouges,
6 boules noires,
4 boules jaunes et
les boules bleues.
On tire une boule au hasard.
Sachant que la probabilité de tirer une boule bleue est égale à
, calculer le nombre de boules bleues.
Réponse
1. La probabilité pour que cette boule soit rouge est:
p(R) =
2. La probabilité pour que cette boule soit noire ou jaune est:
p(N ou J) =
3. La somme des deux probabilités trouvées est:
Le résultat était prévisible puisque p(N ou J) est la probabilité pour que
la boule ne soit pas rouge. Tirer une boule noire ou jaune est
l'évenement contraire (ou complémentaire) de l'événement "tirer une
boule rouge". Ainsi, on aurait ecrit directement p(N ou J) = 1 - p(R) =
.
4. On ajoute dans ce sac x boules bleues. Le sac contient alors (20 + x)
boules au total.
On tire une boule au hasard. La probabilité de tirer une
boule bleue est égale à:
.
Cette équation est équivalente à:
20 + x = 5x. D'où x = 5.
Ainsi, le nombre de boules bleues ajoutées est égal à 5.
11. DNB - Métropole-La Réunion-Mayotte - Juin 2011
Exercice 1
Énoncé
Un dé cubique a 6 faces peintes: une en bleu, une en rouge, une en jaune,
une en vert et deux en noir.
1. On jette ce dé cent fois et on note à chaque fois la couleur de la
face obtenue.
Le schéma ci-dessous donne la répartition des couleurs obtenues
lors de ces cent lancers.
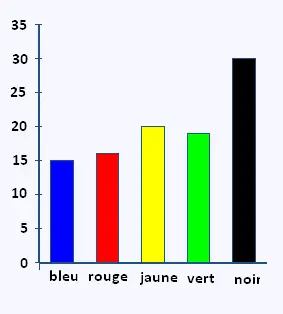
a) Déterminer la fréquence d'apparition de la couleur jaune.
b) Déterminer la fréquence d'apparition de la couleur noire.
2. On suppose que le dé est équilibré.
a) Quelle est la probabilité d'obtenir la couleur jaune?
b) Quelle est la probabilité d'obtenir la couleur noire?
3. Expliquer l'écart entre les fréquences obtenues à la question
1 et les probabilités trouvées à la question 2.
Réponse
a) La fréquence d'apparition de la couleur jaune est ƒ(J) = = 0.20 .
b) La fréquence d'apparition de la couleur noire est ƒ(N) = = 0.30 .
2. On suppose que le dé est équilibré.
a) La probabilité d'obtenir la couleur jaune est p(J) =
b) La probabilité d'obtenir la couleur noire est p(N) =
3. L'écart entre les fréquences obtenues à la question
1 et les probabilités trouvées à la question 2 est due au fait
que, pour un nombre de lancers assez grand, la valeur expérimentale de la
probabilité frequentielle tend vers la probabilité théorique qui est .
Autrement dit:
Si on répète une expérience aléatoire un très grand nombre de fois, la fréquence
d'un événement de cette expérience finit par se stabiliser autour d’un nombre qui est la
probabilité de cet événement.
Dans cet exemple, les fréquences obtenues à la question 1 sont proches
des probabilités calculées à la question 2 (0,2 pour 0,17 et 0,3 pour 0,33).
La différence s'explique par le trop faible nombre de lancers de dés. Si
on continue à jeter ce dé un plus grand nombre de fois (1 000 fois ou 10 000 fois
ou plus), les fréquences obtenues seront quasiment les mêmes que les probabilités
calculées.
12. DNB - Pondichéry - Avril 2011
Exercice 1
Énoncé
Cet exercice est un questionnaire à choix multiples (QCM).
Pour chaque question, une seule réponse est exacte. Aucune justification
n'est demandée. Une réponse correcte rapporte 1 point. L'absence de réponse
ou une réponse fausse ne retire aucun point.
Indiquer sur la copie, le numéro de la question et
la réponse.
2. Un sac contient 10 boules blanches et 5 boules noires. On tire
une boule au hasard. La probabilité de tirer une boule noire est égale à :
a) ,
b) ,
c)
Réponse
2.
a) La probabilité de tirer une boule noire est égale à
13. DNB - Métropole - La Réunion - Mayotte -
Juin 2012
Exercice 1
Énoncé
Pour chacune des deux questions suivantes, plusieurs propositions de
réponse sont faites. Une seule des propositions est exacte.
Aucune justification n 'est attendue.
1. Alice participe à un jeu télévisé. Elle a devant elle trois portes fermées. Derrière
l'une des portes, il y a une voiture ; derrière les autres, il n'y a rien.
Alice doit choisir l'une de ces portes. Si elle choisit la porte derrière laquelle il
y a la voiture, elle gagne cette voiture.
Alice choisit au hasard une porte. Quelle est la probabilité qu'elle gagne la voiture ?
a) ,
b) ,
c) ,
d) On ne peut pas savoir
2. S'il y a quatre portes au lieu de trois et toujours une seule voiture
à gagner, comment évolue la probabilité qu'a Alice de gagner la voiture ?
a) augmente b) diminue c) reste identique d) On ne peut pas savoir
Réponse
1. b)
2. b) diminue.
14. DNB - Polynésie Française - Juin 2012
Exercice 3
Énoncé
L'hôtel "Ia ora na" accueille 125 touristes :
• 55 néo-calédoniens dont 12 parlent également anglais.
• 45 américains parlant uniquement l'anglais.
• Le reste étant des polynésiens dont 8 parlent également anglais.
Les néo-calédoniens et les polynésiens parlent tous le français.
1. Si je choisis un touriste pris au hasard dans l'hôtel, quelle
est la probabilité des événements suivants :
a) Evénement A : "Le touriste est un américain".
b) Evénement B : "Le touriste est un polynésien ne parlant pas anglais".
c) Evénement C : "Le touriste parle anglais"
2. Si j'aborde un touriste dans cet hôtel, ai-je plus de chance de me faire
comprendre en parlant en anglais ou en français ? Justifie ta réponse.
(Toute trace de recherche, même incomplète sera prise en compte
dans l'évaluation).
Réponse
1. Si je choisis un touriste pris au hasard dans l'hôtel,
la probabilité de :
a) L'événement A est:
p(A) = .
b) L'événement B est
p(B) =
c) L'événement C est:
p(C) =
2. La probabilité qu'un touriste parle anglais est:
p(C) = . Ainsi la
probabilité qu'un touriste parle français est
On a:
Donc, si j'aborde un touriste dans cet hôtel, j'ai plus de chance de me faire
comprendre en parlant en anglais qu'en français.
15. Brevet des collèges Métropole septembre 2009
Exercice 2
Énoncé
Pour un tirage au hasard, on a placé dans une urne 25 boules de même taille, les
unes blanches, les autres noires. La probabilité de tirer une boule blanche est 0.32.
Quelles sont les boules les plus nombreuses dans l’urne : les blanches ou les noires ?
Expliquer.
Réponse
Dans l'urne il n'y a 25 boules. Ces boules sont soit blanches soit noires. Ainsi
la probabilité p(N) de tirer une boule noire est complémentaire à la probabilité
p(B) de tirer une boule blanche. C'est à dire: p(B) + p(N) = 1.
Donc p(N) = 1 - p(B) = 1 - 0.32 = 0.68
Nous avons donc: p(N) = 0.68 > p(B) = 0.32 . Il y a donc plus de
noires que de blanches.
Le nombre de boules noires est égal à 0.68 x 25 = 17.
Celui des boules blanches est égal à 25 - 17 = 25 x 0.32 = 8.
Dans l'urne, il y a 17 boules noires et 8 boules blanches.
| | ||||||||||||||
|
||||||||||||||
| | ||||||||||||||
| | ||||||||||||||
| |
||||||||||||||