Mathématiques 2: Probabilités
Langage ensembliste
Événements complémentaires
Évements compatibles et incompatibles.

1. Intersection de deux ensembles

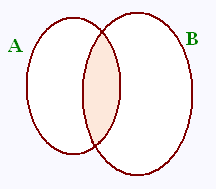
L'intersection de deux ensembles est l'ensemlble qui contient les élements communs à ces deux ensembles.

Si l'ensemble A = {1,2,3,4} et l'ensemble B = {2,4,6,7}, les éléments communs aux ensembles A et B sont {2,4}. Ainsi l'intersection des ensembles A et B est l'ensemble C = {2,4}.

On ecrit A ∩ B = C. Le symbol ∩ se lit inter ou intersection.

Dans le diagramme de Venn, l'intersection des deux ensembles A et B correspond à la partie coloriée.

2. Réunion de deux ensembles

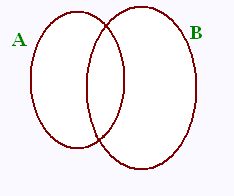
La réunion de deux ensembles est l'ensemlble qui contient tous les élements de ces deux ensembles.

Si l'ensemble A = {1,2,3,4} et l'ensemble B = {2,4,6,7}, tous les élements de ces deux ensembles sont {1,2,3,4,6,7}. Ainsi la réunion des ensembles A et B est l'ensemble D = {1,2,3,4,6,7}.

On ecrit A ∪ B = D. Le symbol ∪ se lit union.

Dans le diagramme de Venn, l'union des deux ensembles A et B correspond à la partie coloriée.

2. Événements complémentaires

On considère un ensemble de référence R = {1,2,3,4,5,6,7,8,9}. La pr

obabilité de l'événement obtenir un nombre pair est 4/9.

La probabilité de l'événement obtenir un nombre impair est 5/9.

La somme des probabilités des événements est égale à 1.

On dit que l'événement obtenir un nombre pair est le complément de l'événement obtenir un nombre impair

3. Compatibilité des événements

Lors d'une expérience aléatoire, si aucun des résultats d'un événement A ne corresponde à des résultats d'un événement B, alors les deux événements sont incompatibles.

Lors d'une expérience aléatoire, si au moins un des résultats d'un évenement A corresponde à des résultats d'un évenement B, alors les deux événements sont compatibles.

Les évenements obtenir un nombre pair et obtenir un nombre impair sont incompatibles car ils ne possèdent aucun résulat commun.

Les événements obtenir un nombre pair et obtenir un nombre divisible par 3 sont compatibles car ils possèdent au moins un résulat commun.

Les événements obtenir un nombre impair et obtenir un nombre divisible par 3 sont compatibles car ils possèdent au moins un résulat commun.

4. Probabilité des événements compatibles

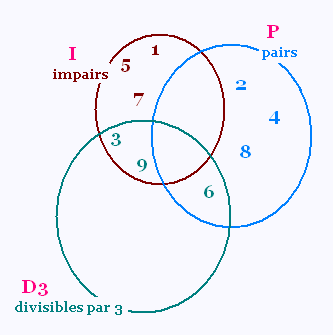
Dans l' ensemble de référence R = {1,2,3,4,5,6,7,8,9}.

Pour simplifier l'ecriture, on pose

Ep : l'évenement obtenir un nombre pair,
Ei : l'évenement obtenir un nombre impair,
Ed3: l'évenement obtenir un nombre divisible par 3.

Il n' ya aucun résultat commun aux évenements Ep et Ei.

Le résultat commun aux évenements Ep et Ed3 est 6.

Les résultats commun aux évenements Ei et Ed3 sont 3 et 9.

Dans le diagramme de Venn, il y a 6 nombres dans l'ensemble P ∪ I = {2,4,8,6,9,3}, ainsi
La probabilité de l'événement obtenir un nombre pair ou ou un nombre disisible par 3 est: 6/9.

Donc, dans l'ensemble de référence R, La probabilité de l'événement obtenir un nombre pair ou ou un nombre disisible par 3 est: 6/9

Cette probabilité est égale aussi à
. la probabilité de l'événement:
obtenir un nombre pair +
. la probabilité de l'événement obtenir un nombre disisible par 3 -
. la probabilité de l'événement obtenir un nombre à la fois pair et disisible par 3 qui est: 1/9.

C'est à dire

4/9 + 3/9 - 1/9 = 6/9

On ecrit d'une façon générale:

P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

5. Exemple: Jeu de 52 cartes

le jeu de 52 cartes est un jeu de cartes qui contient 52 cartes organisées en deux enseignes ou couleurs: le noir et le rouge.

Le noir comporte 13 cartes de piques et 13 cartes trèfles.

Le rouge comporte 13 cartes coeur et 13 cartes carreaux.

Les 13 cartes de chaque série, qui est en nombre de 4, 2 series rouges et deux séries noirs, sont marquées de treise valeurs:
As, 2, 3, 4, 5, 6, 7, 8, 9, 10, Valet, Dame, et Roi.

La carte figure J (jack) est dite Valet qui signifie serviteur,
La carte figure Q (queen) est dite dame,
La carte figure K (king) est dite roi.

En somme, il ya :

- 52 cartes en tout,
- 13 valeurs: 1,2,3,4,5,6,7,8,9,10,V,D,R,
- 13 valeurs noires pique,
- 13 valeurs noires trèfle,
- 13 valeurs rouges coeur,
- 13 valeurs rouges carreau,
- 2 x 13 = 26 cartes noires,
- 2 x13 = 26 cartes rouges,
- 10 x 4 = 40 cartes chiffres,
- 3 x 4 = 12 cartes figures

L'expérience aléatoire que l'on considère consiste à tirer au hasard une seule carte.

On considère les 4 évenements suivants:

A: Tirer une carte noire
B: Tirer une dame
C: Tirer une carte de coeur
D: Tirer une figure

Nous avons:

P(A) = 26/52 = 1/2
P(B) = 4/52 = 1/13
P(C) = 13/52 = 1/4
P(D) = 12/52 = 3/13

P(A ∩ B) = P(dame noire) = 2/52 = 1/26
= P(A) x P(B) = 1/2 x 1/13 = 1/26

P(B ∩ C) = P(dame de coeur) = 1/52
= P(B) x P(C) = 1/13 x 1/4 = 1/52

P(A ∩ C) = P(noire de coeur) = 0/52
Tous les coeurs sont rouges.
P(Φ) = 0

P(C ∩ D) = P(figure de coeur) = 3/52

P(A ∩ B ∩ C) = P(dame noire de coeur) = 0/52
Tous les coeurs sont rouges
P(Φ) = 0

P(A ∪ B) = P(une noire ou une dame) =
P(une noire) + P(une dame) - P(noire et dame)
26/52 + 4/52 - 2/52 = 28/52 = 7/13

P(C ∪ D) = P(une figure ou un coeur) =
P(une figure) + P(un coeur) - P(figure et coeur)
12/52 + 13/52 - 3/52 = 22/52 = 11/26

P(A ∪ B ∪ C) = P(une dame noire de coeur) =
P(A ∪ B) + P(C) - P((A ∪ B) ∩ C)

Avec:

P(A ∪ B) = P(A) + P( B) - P(A ∩ B)
(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
P((A ∩ C) ∪ (B ∩ C))
= P((A ∩ C)) + P(B ∩ C) - P(A ∩ C ∩ B ∩ C)

On obtient:

P(A ∪ B ∪ C) = P(A) + P( B) + P(C) - P(A ∩ B)
- P((A ∩ C)) - P(B ∩ C) + P(A ∩ C ∩ B ∩ C)
= 1/2 + 1/13 + 1/4 - 1/26 - 0 - 1/52 + 0 = 40/52 = 10/13.

6. Exercices

6.1. Exercice 1

Dans une classe, il y a 22 élèves; 12 d'entre eux parlent anglais, 10 parlent français, 8 parlent l'espagnol, 6 parlent anglais et français, 5 parlent anglais et espagnol, 4 parlent français et espagnol, et 2 parlent les trois langues.

Choisi au hasard, quelle est la probabilité qu'un élève:

a) parle anglais ?
b) parle anglais et espagnol ?
c) ne parle que l'anglais ?
d) ne parle que l'espagnol ?
e) parle français ou anglais ?
f) parle une des trois langues ?

6.2. Exercice 2: Probabilité par mesure

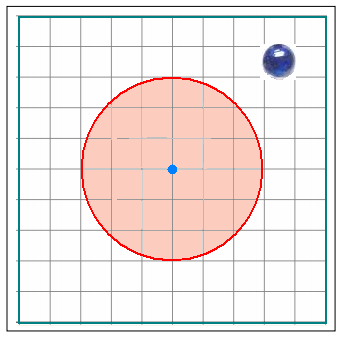
On lance une bille sur table quadrillée où on a dessiné un cercle.

Un carreau représente une unité.

L'expérience aléatoire consiste à compter le nombre de fois la bille s'est stabilisée à l'intérieur du cercle ou le nombre de fois à l'extérieur du cercle tout en restant dans le carré.

a) Quel est la brobabilité que la bille se stabilise à l'intérieur du cercle ?

b) Si on fait 50 lancements, quel sera le nombre de fois la bille set stabiliserait à l'intérieur du cercle ?