Mathématiques 2: Probabilités, analyse combinatoire
& loi binomiale

Dé tétraédrique et loi binomiale

1. Les astragales

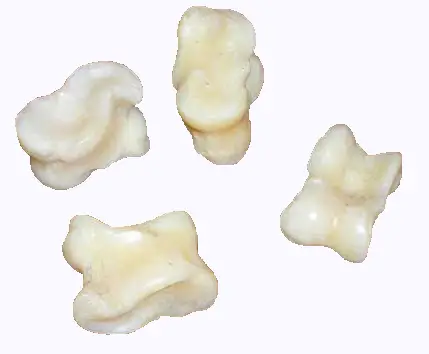
Un osselet est un petit os. L'astragale est un osselet d'articulation qu'on trouve dans le tarse du carpe (squelette du poignet) de pattes arrières du mouton ou de la chèvre.

Dès l'antiquité, Les Grecs et les Romains utilisaient ces osselets pour le jeu au dés. Aujourd'hui ils sont fabriquées en métal ou en plastique.

Un astragale présente quatre faces d’un aspect différent : deux de faces larges, l’une est convexe, l’autre concave et des deux plus étroites, l’une est plate, l’autre sinueuse.

On attribuait des valeurs aux faces d'un astragale et pariait sur les sommes des nombres des faces obtenues:

La face plate "planum" vaut 1,
La face concave (creux) "supinum" vaut 3,
La face convexe (bosse)"pronum" vaut 4,
La face sinueuse "tortuosum" vaut 6.

2. Le jeu des osseletes

Du point de vue probabilités, on attribue des numéros aux faces d'un astragale:

La face 1 est plate "planum" ,
La face 2 est concave (creux) "supinum",
La face 3 est convexe (bosse)"pronum",
La face 4 est sinueuse "tortuosum",


Un astragale n'est pas un jeu pipé. Il est naturellement un objet qui n'est pas sysmétrique. Si on le lance et on note la face obtenue, les évenements obtenir une face parmi les quatres de l'osselet, de cette expérience aléatoire ne sont pas équiprobables.

L'expérience montre que si p1, p2, p3, et p4 sont les probabilités d'obtenir, après lancer, respectivemenet les faces 1, 2, 3, et 4, alors:

p1 = p2, p3 = p4 et p1 = 4p3.

La face plate et la face sinueuse ont 4 fois moins de chance d'apparaitre comme résultat après un lancer que les faces larges.

3. Applications

On lance un astragale.

Pour un premier lancer, l'univers des possibilités est Ω = {1, 2, 3, 4}.

La loi de probabilité, Σpi = 1, permet d'ecrire:

p1 + p2 + p3 + p4 = 1

En utilisant les résultats expérimentaux plus haut, on trouve:
2pi + 2p3 = 1
2p1 + 2 (p1/4) = 1

Donc

p1 = 2/5 = p2
p3 = p4 = 1/10

a) Combien a-t-on d'éventualités après un seul lancer d'un seul astragale?

b) On considère l'événement A: obtenir un nombre impair Quelle est la probabilité d'avoir cet évenement?

c) On considère l'événement B: obtenir un supinum ou un pronum Quelle est la probabilité d'avoir cet évenement?

d) On considère l'événement C = A: obtenir un nombre pair, un supinum ou un pronum Quelle est la probabilité d'avoir cet évenement?

e) Combien a-t-on d'éventualités après deux lancers d'un seul astragale?

f) Combien a-t-on d'éventualités après 7 lancers d'un seul astragale?

g) Quelle est la probabilité d'avoir une seul tortuosum au cours de 4 lancers?

h) Quelle est la probabilité d'avoir 4 planum au cours de 3 lancers?

i) Quelle est la probabilité d'avoir 4 planum au cours 10 lancers?

j) Quelle est la probabilité d'avoir 2 planum 2 supinum, 3 pronum et 4tortuosum au cours de 10 lancers?