probabilités applications
Mathématiques 2:
Probabilités
Résumé et applications
I. Résumé
Une probabilité est un
nombre réel, positif et plut petit
ou égal à 1, qui quantifie la chance
qu'un évenement se produise lors
d'une expérience
aléatoire.
Exemple:
Dans un sac il y a 9 billes au total. 4 jaunes,
3 blues, et 2 rouges. Si on tire 1 bille
au hasard, quelle est la probabilité qu'elle soit
jaune?
aléatoire = dont on ne peut pas prévoir le résultat de façon certaine.
1. Probabilité théorique

La probabilité théorique de l'événement A est égale à
P(A) = (nombre de résultas favorables à A)/( nombre de résultas possibles)
On lance un dé cubique. La probabilité d'avoir
un "quatre" est égale à 1/6.
2. Probabilité conditionnelle

La probabilité conditionnelle de A sachant B est
égale à:
P(A|B) = P(A ∩ B)/P(B)
Avec P(B) ≠ 0.
Quelle est la probabilité de tirer un "roi" d'un jeu de 52 cartes,
sachant que la carte est une figure rouge?
2. Probabilité géométrique
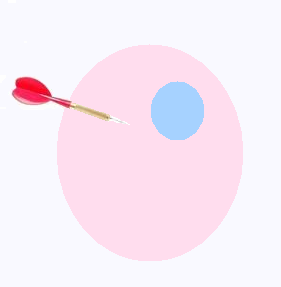
La probabilité géométrique est le rapport de la mesure des
figures géométriques favorables à l'expérience aléatoire et de celle
des figures géométriques possibles.
P(A dans B) = mes (A)/(mes (B)
Quelle est la probabilité que la flèche tombe
sur le cercle bleue?
2. Probabilité fréquentielle

La probabilité fréquentielle est le rapport des effectifs
favorables à l'expérience aléatoire et de ceux
des effectifs possibles.
P(A) = effectis(A)/(total des effectifs)
C'est aussi
(nombre de fois que le résultat attendu s’est réalisé)/(
nombre de fois que l’expérience a été répétée)
Dans une bibliothèque, nous avons 9 livres jaunes,
10 rouges et 6 blancs.
Quelle est la probabilité de tirer un livre rouge?
II. Exercices

Exercice 1
Question:

Sur une urne, il y a 4 billes toutes de la même
taille. Un bille en cuivre jaune, une bille en cuivre
rouge, une bille en argent jaune et une bille en bronze
rouge.
On pige une bille au hasard dans cette urne.
a) Quelle est la probabilité de l'évenement "avoir une bille jaune"?
b) Quelle est la probabilité de l'évenement "avoir une bille rouge"?
c) Quelle est la probabilité de l'évenement "avoir une bille en cuivre"?
d) On désigne par:
A l'évenement "avoir une bille jaune",
B l'évenement "avoir une bille rouge", et
C l'évenement "avoir une bille en cuivre"
Ces évenements sont-ils indépendants?
Réponse:
Il s'agit d'une probabilité d'événements
compatibles ou incompatibles; dépendants ou indépendants .
a) P(A) = 2/4 = 1/2
b) P(B) = 2/4 = 1/2
c) P(C) = 2/4 = 1/2
d) 1.
Probabilité d'avoir une bille à la fois jaune et rouge =
P(A ∩ B) = 0 puisque le nombre de cas favoravles
est égal à zéro. C'est même impossible.
Les événements A et B sont incompatibles.
A ∩ B = Φ ou {}.
Ces événements sont aussi dépendants puisque la
réalisation de l'un influe sur celle de l'autre.
On a de même P(A ∩ B) ≠ P(A) x P(B)
2.
Probabilité d'avoir une bille rouge en cuivre n'est pas nulle
puisque ça correspond à un événement possible. Cette
probabilité st égale à
P(B ∩ C) = 1/4.
Les événements B et C sont compatibles.
Ces événements sont aussi indépendants puisque la
réalisation de l'un n'influe pas sur celle de l'autre.
3.
Probabilité d'avoir une bille jaune en cuivre n'est pas nulle
puisque ça correspond à un événement possible. Cette
probabilité st égale à
P(A ∩ C) = 1/4.
Les événements A et C sont compatibles.
Ces événements sont aussi indépendants puisque la
réalisation de l'un n'influe pas sur celle de l'autre.
4.
P(A ∩ B ∩ C) = 0
Les événements A B, et C sont incompatibles et
globalement ne sont pas indépendats.
Exercice 2
Question:
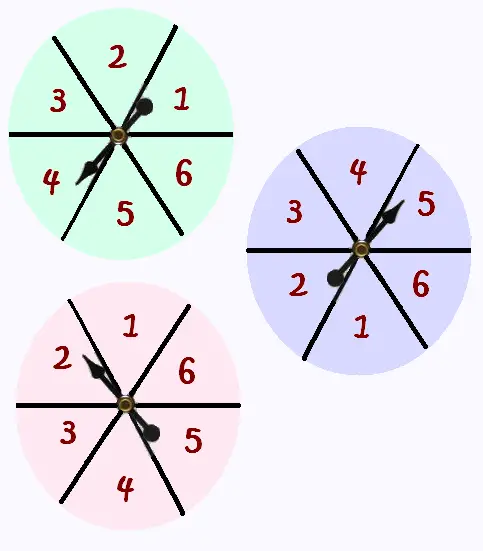
On fait tourner trois roulettes identiques une seule
fois.
On observe les chiffres obtenus.
a) Quel est le nombre de résultats possibles
en tenant compte de l'ordre?
b) Quel est le nombre de résultats possibles
sans tenir compte de l'ordre?
c) Quelle est la probabilité d'avoir le "1 1 1" ?
d) Quelle est la probabilité d'avoir le "2 4 6" ?
e) Quelle est la probabilité d'avoir le "1 1 1",
ou le "2 2 2" ou le "5 5 5 " ?
Réponse:
Tout se passe comme si on tourne une roulette
trois fois de suite.
Tout se passe comme si on lance un dé cubique
trois fois de suite.
Tout se passe comme si on fait trois tirages au sort
succéssifs avec remise d'une bille d'une urne qui
en contient 6.
a) Avec ordre = arrangement avec remise =
np = 63 = 216
b) Sans ordre = combinaisons avec remise =
D(3,6) = (6 + 3 - 1)!/3!(6 - 1)! = 8!/3!5! = 56
c) La probabilité d'avoir le "1 1 1" est
(1/6)3 = 1/216 = 0.5%
d) La probabilité d'avoir le "2 4 6" est
(1/6)3 = 1/216 = 0.5%
e) La probabilité d'avoir le "1 1 1",
ou le "2 2 2" ou le "5 5 5 " est
(1/6)3 + (1/6)3 + (1/6)3 = 3/216
= 1.0 %.
Exercice 3
Question:
Un sac contient 5 lettres: A, B, C, D, et E.
On tire les lettres au hasard sans remise.
Quel est le nombre de mots différents que
l'on peut former si l'on tire:
a)3 lettres?
b)4 lettres?
c)5 lettres?
Réponse:
Différent veut dire avec ordre .
Il s'agit donc d'une expérience aléatoire
avec ordre et sans remise
Les nombres checrchés sont des arrangements
sans remise A(p,n) = n!/(n - p)! de p (= nombre de
lettres du mot à former) parmi 5 dans l'univers
considéré Ω = {A, B, C, D, E}.
a) A(3,5) = 5!/ 2!= 3 x 4 x 5 = 60
b) A(4,5) = 5!/1! = 5! = 120
b) A(5,5) = Permutations des 5 lettres = 5! = 120.
Exercice 4
Question:
On tire quatre cartes d'un jeu de 52 cartes
sans tenir compte de l'ordre et sans remise.
Quelle est la probabilité de former une main
de 4 valets?
Réponse:
Il s'agit donc d'une expérience aléatoire
sans ordre et sans remise, et donc d'une combinaison.
On note bien que la probabilité d'avoir quatre valets
est la même que la probabilité d'avoir n'importe quel carré.

La probabilité d'avoir un valet
- au premier tirage est (4/52),
- au deuxième tirage (3/51),
- au troisième tirage (2/50), et enfin
- au quatrième tirage (1/49)
Donc en tout, en a (4/52)x(3/51)x(2/50)x(1/49) = 0.0000037
Cette probabilité est celle du valet. C'est aussi celle
de tout carré.
Comme il peut s’agir de n’importe quel carré (13 carrés possibles),
on aura
P(carré1) + P(carré2) + P(carré2) ... + P(carré13) =
= 13 x P(n'importe quel carré).
La probabilité d'avoir un carré "4 dames" est 0.000003694.
La probabilité d'avoir un carré 13 x 0.0000037 = 0.000048.
Le carré est précisé → Po = 0.000003694
Le carré est non précisé → P = 13 Po = 0.000048
D'une autre façon:
Il y a une possibilité sur 13 d'avoir une valeur.
Dans cette possibilité, il y en a quatre
avec les 4 suites. Donc C(1,13) C(4,4) en tout.
Ainsi
Le nombre de combinaisons possibles d'avoir un
carré est
C(1,13) C(4,4) = 13
La probabilité d'avoir un carré est égale à
C(1,13) C(1,4) /C(4,52) = 13 x 0.000003694.
C'est à dire 13 fois la probabilité d'un carré
spécifié.
On note que:
0.000003694 = 1/C(4.52)
Exercice 5

Question et réponses: Jeu de 52 cartes
1) On tire une carte. Quelle est la probabilité d’obtenir
un trèfle ou un roi ?
On a 13 cartes de trèfle en tout aux quelles il faut ajouter
les 3 rois qui ne sont pas des trèfles.
La probabilité cherchée est égale à
13/52 + 3/52 = 16 / 52 = 0,3077.

2) On tire une carte. Quelle est la probabilité que ce soit une figure de couleur rouge ?
Il existe 6 figures de couleur rouge, 6 cartes favorables sur 52
possibles. Donc
La probabilité cherchée est égale à 6 / 52 = 0,1154.
3) On tire une carte. Quelle est la probabilité que ce soit une dame de pique si l’on sait qu’il s’agit d’une carte noire ?
Il existe 26 cartes noires et 1 dame de pique. La probabilité conditionnelle (dame de pique|carte noire) est égle à
1/26 = 0,0385.
4) On tire au hasard deux cartes. Quelle est la probabilité
que ce soit deux cartes As?
Au premier tirage la probabilité d’avoir un As est 4 / 52.
Au deuxième tirage et sachant qu’un As ait déjà été tiré,
il reste 3 As sur 51 cartes.
La probabilité conditionnelle est égale à
(4/52) x (3/51) = 0,00452.
5) On tire au hasard une carte, puis une deuxième sans
remettre la première, quelle est la probabilité que la deuxième
soit un valet si la première était une dame ?
Le tirage d’une dame modifie la probabilité de tirage d’un valet au deuxième tirage car il reste 51 cartes au lieu de 52 et 4 valet puisqu’aucun n’a été retiré au premier tirage.
La probabilité conditionnelle est donc égale à
4 / 51 = 0,07843.
6) On tire au hasard une carte, puis une
deuxième sans remettre la première. Quelle est la probabilité que la deuxième soit un roi si la première l’était aussi ?
Au deuxième tirage, il reste 3 rois dans les 51 cartes. La probabilité conditionnelle est égale à
3 / 51 = 0,0588.
7) On tire au hasard et successivement trois cartes en replaçant
les cartes dans le jeu après chaque tirage. Quelle est la probabilité d’obtenir 3 dames ?
A chaque tirage la probabilité d’obtenir une dame est égale à 4 / 52 = 0,0769.
Comme les évènements sont indépendants c’est-à-dire que la probabilité d' avoir une dame à un tirage donné ne dépend pas des résultats des tirages précédents, la probabilité est égale à
(4/52) x (4/52) x (4/52) = x 4 x 4)/(52 x 52 x 52) = 0,000455.
Exercice 6
Question:
Dans une urne, il y a 17 billes. 5 vertes et 12 rouges.
On tire au hasard une après l'autre pour former un
groupe de 4 billes.
a) Quelle est la probabilité que les deux premiers tirages
donnent deux vertes?
b) Quelle est la probabilité que le groupe de 4 billes
soit, dans l'ordre, formé par deux vertes, ensuite une
rouge et finalement une autre verte ?
c) Est ce que toutes les fçons de constituer
ce groupe ont la probabilité de se réaliser?
Réponse:
a) P(V,V) = (5/17) x (4/16)
b) P(V,V) = (5/17) x (4/16) x (12/15) x (3/14)
c) Toutes les possibilités n'ont pas
la même probabilité de se réaliser puise
les billes sont différentes en effectis de départ.
Exemple Pour former un groupe de 4 rouges, la
probabilité est de (12/17) x (11/16) x (10/15) x (9/14)
qui est différente de celle trouvée en c)
Exercice 7
Question:
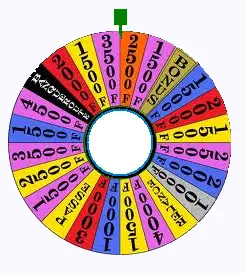
Dans une roue de fortune de 24 secteurs, les chances de
gagner sont équiprobables. On tourne la roue une seule fois.
a) Quelle est la probabilité que ça tombe sur un bonus?
b) Quelle est la probabilité que ça tombe sur un bonus ou
un passe?
Si la roue contenait moitié fois moins de secteurs,
c) Quelle est la probabilité que ça tombe sur une bonus ?
d) Quelle est la probabilité que ça tombe sur une relance
et un bonus?
Réponse:
a) P(bonus) = 1/24 = 4.17%
b) P(bonus ou passe) = 1/24 + 1/24 = 2/24 = 8.33%
c) P(bonus) = 1/(24/2) = 2/24 = 2 x 1/24 = 8.33%
Mois il ya de secteurs, plus les chances de gagner sont
grandes.
d) P(relance ou bonus) = 1/12 + 1/12 = 2/12 = 16.7%
Exercice 8
Question:
Quelle est la probabilité de tirer un "roi" d'un jeu de 52 cartes,
sachant que la carte est une figure rouge?
Réponse:
Il s'agit d'une probabilité conditionnelle.
Soit A l'événement "la carte tirée est un roi",
B l'événement "la carte tirée est une figure rouge".
la probabilité P(A) de tirer un "roi" d'un jeu de 52 cartes
est égale à 4/52 = 1/13 .
la probabilité P(B) de tirer une "figure rouge" d'un jeu de 52 cartes
est égale à 6/52 .
Si on sait que c'est une figure rouge, la probabilité P(A)
devient P(A sachant B) = P(A/B) = 2/6 = 1/3.
la probabilité P(A ∩ B) de tirer une "roi rouge" d'un jeu
de 52 cartes est égale à 2/52 .
P(A/B) = P(A ∩ B)/P(B) = (2/52)/(6/52)= 2/6 = 1/3
= 0.33
La probabilité de tirer un "roi" d'un jeu de 52 cartes,
sachant que la carte est une figure rouge est de 33.33%.
Exercice 9
Question:
Dans une bibliothèque, nous avons 9 livres jaunes,
10 rouges et 6 blancs.
a) Quelle est la probabilité de tirer un livre rouge?
a) Quelle est la probabilité de tirer d'abord un livre
et puis ensuite un jaune?
Réponse:
Il s'agit d'une probabilité fréquentielle.
Soit R l'événement "tirer un livre rouge". Son effectif est de
10.
L'effectif total est 9 + 10 + 6 = 25.
la probabilité P(R) de tirer un "livre rouge" d'une
biliothèque de 25 livres est égale à
P(R) = (Effectif de R)/(effectif total) = 10/25 = 2/5 .
la probabilité P(J) de tirer une "deuxième livre", mais
jaune cette fois-ci est égale à
P(J) = (Effectif de J)/(effectif total) = 9/24 = 3/8 .
la probabilité P(RJ) de tirer un "rouge", puis ensuite un
"jaune" est égale à
P(RJ) = P(R) x P(J) = (2/5) x (3/8)= 3/20 = 15% .
Exercice 10
Question:
Au jeu de poker, quelle est la probabilité
d'avoir un carré?
Un carré poker ou "Four of a kind" est une main
formée avec 4 cartes de même valeur en plus d'
une autre carte.
Réponse:
Il s'agit d'une probabilité combinatoire
sans remise et sans ordre.
Le carré se compose de toutes les quatres
suites pour un certaine valeur. La cinquième est
une carte d'une autre valeur.
Il y a une possibilité sur 13 d'avoir une valeur.
Dans cette possibilité, il y en a C(1,4) = 4
avec les 4 suites. Donc C(1,13) C(1,4) en tout.
Pour l'autre carte, c'est à dire la cinquième avec
une autre valeur, il y a une possibilité sur 12 avec
4 suites, soit C(1,12) C(1,4).
Ainsi
Le nombre de combinaisons possibles d'avoir un carré
est C(1,13) C(1,4) . C(1,12) C(1,4) = 624
La probabilité d'avoir un carré est égale à
C(1,13) C(1,4) . C(1,12) C(1,4) /C(5,32) = 0.024 %
Exercice 11
Question:
Nous avons 3 urnes.
La première U1 contient
10 billes dont 10% sont blanches, la deuxième U2 contient
20 billes dont 20% sont blanches, et la troisième U3 contient
30 billes dont 30% sont blanches.
On vide toutes les trois urnes U1, U2, et U3
dans une grande urne U, et on tire
au hasard une bille.
Quelle est la probabilité de tomber sur une
blanche qui provient de l'urne U2?
Réponse:
Il s'agit d'une probabilité conditionnelle .
On désigne les événements ainsi:
E1: "la bille provient de l'urne U1"
E2: "la bille provient de l'urne U2"
E3: "la bille provient de l'urne U3"
B: "la bille est blanche".
On cherche la probabilité P(U2|B), c'est à dire
la brobabilité que la bille provienne de U2
sachant qu'elle est blanche.
La probabilité d'avoir une bille qui
provient de l'urne U1 est égale à
P(U2) = 10/(10 + 20 + 30) = 10/60 = 1/6.
La probabilité d'avoir une bille qui
provient de l'urne U2 est égale à
P(U2) = 20/(10 + 20 + 30) = 20/60 = 1/3.
La probabilité d'avoir une bille qui
provient de l'urne U3 est égale à
P(U2) = 30/(10 + 20 + 30) = 30/60 = 1/2.
La probabilité d'avoir une bille blanche
sachant qu' elle provient de l'urne
U1 est égale à
P(B|U1) = 1/6 x 10% = 1/60.
La probabilité d'avoir une bille blanche
sachant qu' elle provient de l'urne
U2 est égale à
P(B|U2) = 1/3 x 20% = 4/60.
La probabilité d'avoir une bille blanche
sachant qu' elle provient de l'urne
U3 est égale à
P(B|U3) = 1/2 x 30% = 9/60.
On admet que
La probabilité d'avoir une bille blanche
sachant qu' elle provienne de l'urne
U2 est égale à la probabilité d'avoir une bille
qui provient de l'urne U2 sachant qu' elle
est blanche.
Nous avons:
P(B|U1) = P(U1|B) = 1/60
P(B|U2) = P(U2|B) = 4/60
P(B|U3) = P(U3|B) = 9/60
La probilité totale d'avoir une blanche est égale à
P(B) = (1/60) + (4/60) + (9/60) = 14/60
Ainsi la probabilité cherchée est
P = P(B|U2)/P(B) = (4/60)/(14/60) = 4/14 = 2/7 = 28.57%
Exercice 12
Question:

Dans une bibliothèque, il y a 30 ouvrages: 7 livres d'histoire,
5 romans, 8 recueils de poems, 4 dictionnaires, et des guides
de jardinage et de bricolage.
On prend un ouvrage au hasard.
a) Quelle est la probabilité d'avoir un roman?
b) Quelle est la probabilité d'avoir un livre
d'histoire ou un dictionnaire?
c) Quel sont les nombres de guides sur le jardinage
et sur le bricolage si la probabilité d'avoir un guide
de jardinage est 2/15?
Réponse:
a) La probabilité d'avoir un roman est 5/30 = 1/6
b) La probabilité d'avoir un livre
d'histoire ou un dictionnaire est égale à 7/30 + 4/30 = 11/30
c) Les guides sont en nombre de 6. Si la probabilité d'avoir
un guide de jardinage est 2/15, alors
2/15 + x/30 = 6/30 → x = 2
x est le nombre de guides sur le bricolage.
y = 6 - 2 = 4 est le nombre de guides sur
le jardinage.
Exercice 13
Question:

On tire à trois reprises une pièce de monnaie d'un
prte monnaies qui contient 6 pièces de 1$;, 4 pièces
de 2$ et 9 pièces de 25¢.
On remet la monnaie tirée dans le porte-monnaie après
chaque tirage.
a) Construire le diagramme en arbre qui représente cette situation.
b) Quelle est la probabilité de tirer une pièce de 2$
3 fois de suite?
c) Quelle est la probabilité de tirer une pièce de 25¢,
suivie d'une pièce de 1$ et encore d'une pièce de 1$ ?
d) Quel est l'événement qui le plus de chance de ce réaliser?
e) Quel est l'événement le moins probable?
Réponse:
a)
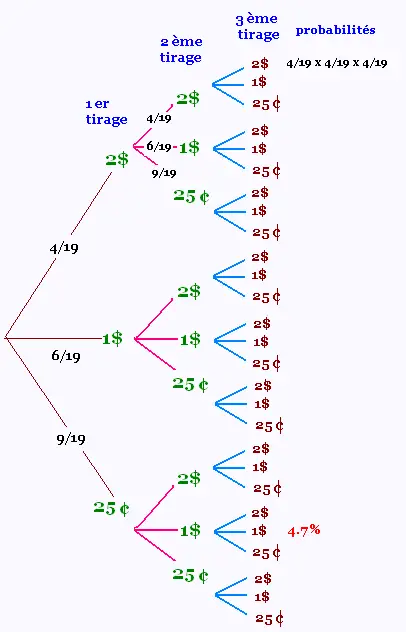
b) P(2$ 2$ 2$) =
(4/19) x (4/19) x (4/19) = 0.9%
c) P(25¢ 1$ 1$) =
(9/19) x (6/19) x (6/19)= 4.7%
d) P(le plus probable) = P(le plus grand numérateur)
Du côté des pièces 25 ¢ → plus grand numérateur c'est 9 x 9 x 9 . Donc
P(le plus probable) = 9 x 9 x 9 /19 x 19 x 19 = 10.63%
e) P(le moins probable) = P(le plus petit numérateur)
Du côté des pièces 2$ → plus petit numérateur c'est 4 x 4 x 4 . Donc
P(le plus probable) = 4 x 4 x 4 /19 x 19 x 19 = 0.9%.
Exercice 14
Question:
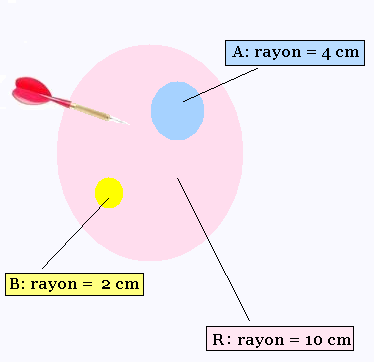
On lance la fléchette dans le but d'atteindre
un cercle parmi le cercle A de rayon 4 cm ou
le cercle B de rayon 2cm.
a) Quelle est la probabilité que la fléchette
atteigne le cercle de référence R?
b) Quelle est la probabilité que la fléchette
atteigne le cercle A?
c) Quelle est la probabilité que la fléchette
atteigne le cercle B?
d) Quelle est la probabilité que la fléchette
atteigne le cercle A ou le cercle B?
e) Quelle est la probabilité que la fléchette
atteigne l'espace complémentaire au cercle A et B?
Réponse:
a) La probabilité que la fléchette
atteigne le cercle de référence de
rayon 10 cm est égale à
P(R) = (aire du cercle R)/ (aire du cercle R) = 1
b) La probabilité que la fléchette
atteigne le cercle A est égale à
P(A) = (aire du cercle A)/ (aire du cercle R) =
π(4)2/π(10)2 = 16/100 = 16%
c) La probabilité que la fléchette
atteigne le cercle B est égale à
P(B) = (aire du cercle B)/ (aire du cercle R) =
π(2)2/π(10)2 = 4/100 = 4%
d) La probabilité que la fléchette
atteigne le cercle A ou le cercle B est égale à
P(B ou B) = P(B ∪ B) = P(A) + P(B) =
16% + 4% = 20%
e) La probabilité que la fléchette
atteigne l'espace complémentaire au cercle A et B
est égale à
P(R) - (P(A) + P(B)) = 100% - 20% = 80 %.
Exercice 15
Question:
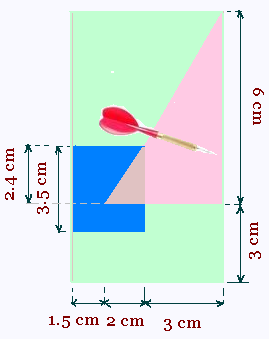
On lance la fléchette dans le but d'atteindre
le triangle commun au triangle et au carré.
a) Quelle est la probabilité que la fléchette
atteigne ce triangle commun?
b) Quelle est la probabilité que la fléchette
atteigne le triangle ou le carré ?
Réponse:
Aire du rectangle de référence =
6.5 x 9 = 58.5 cm2
Aire du triangle =
6 x 5 /2 = 15.0 cm2
Aire du carré =
3.5 x 3.5 = 12.25 cm2
Aire du triangle commun =
2.4 x 2 /2 = 2.4 cm2
a) Le triangle commun est l'intersection
du triangle et du carré. Son aire est
égale à 2.4 cm2
La probabilité que la fléchette
atteigne ce triangle commun est égale à
l'aire du triangle commun/aire du rectangle de
référence =
2.4 cm2 /58.5 cm2 = 4.1%
b) La probabilité que la fléchette
atteigne le triangle ou le carré est égale à
P(triangle) + P(carré) - P(triangle commun) =
15/58.5 + 12.5/58.5 - 2.4/58.5 = 43.0%
On retient:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Exercice 16
Question:

Jim a un dé tétraédrique. Lynda a un dé cubique. Dans une
une urne, il y a des pastilles numérotées 1 à 8.
Les règles du jeu sont les suivantes:
Quelqu'un tire une pastille. On marque le
chiffre de cette pastille.
Ensuite chacun des joueurs lance son dé. Celui
ou celle qui a le même numéro que celui
de la pstille gagne.
Lequel des joueurs a plus de chance de gagner,
Jim ou Lynda?
Réponse:
Pour Jim, les probabilités sont P(J) = 1/4
Pour Lynda les probabilités sont P(L) = 1/6
Pour les pastilles, les probabilités sont P(P) = 1/8
L'événement "obtenir un numéro par la pastille"
a une probabilité de 1/8. Par suite:
Jim a une probabilité de (1/8) x (1/4) = 1/32 = 3.1%
d' avoir le même résultat que celui de la pastille.
Lynda a une probabilité de (1/8) x (1/6) = 1/48 =
2% d'avoir le même résultat que celui de la pastille.
Pour ce jeu, celui qui a un dé avec moins de faces
a plus de chance de gagner
.
Exercice 17
Question:
Voici une partie d'un tableau des prévisions météorologiques de Météo Média pour Montréal
pendant 24 heures en tranches de 6 heures. On
s'interesse aux probabilités de précipitations
pendant ces 24 heures.
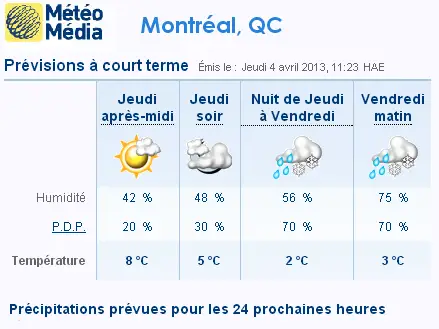
Le terme P.D.P. est l'abréviation utilisée pour probabilité de précipitations.
a) Quelle est la probabilité qu'il pleuve Jeudi après-midi et Jeud soir ?
b) Quelle est la probabilité qu'il pleuve Jeudi après-midi et et Vendredi Matin ?
c) Quelle est la probabilité de n'avoir aucune goutte de pluie pendant ce temps ?
d) Quelle est la probabilité qu'il pleuve Jeudi après-midi ou Vendredi Matin ?
e) Quelle est la probabilité qu'il pleuve au moins une fois pendant cette période de 24 heures ?
f) Quelle est la probabilité qu'il pleuve au plus pendant une des ces 5 périodes ?
À chaque fois qu'il y a x% de chance qu'il pleuve,
il y a (100 - x)% de chance qu'il ne pleuve pas.
Les événements avec x% de chance et (100 - x)% de chance
sont complémentaires.
Les événements "pleuvoir au moins pendant une période", et "ne pas pleuvoir du tout" sont complémentaires.
Voici le diagramme en arbre des probabilités:
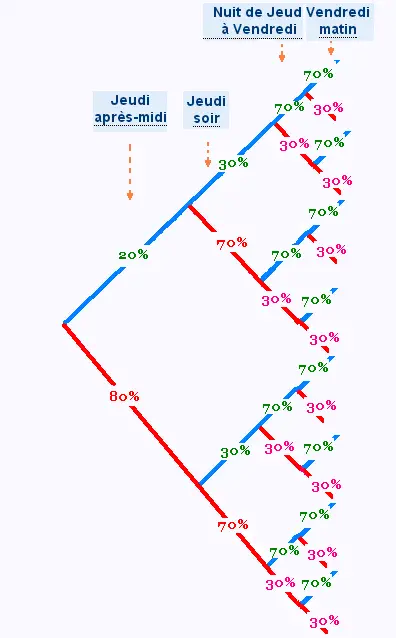
a) La probabilité qu'il pleuve Jeudi après-midi et Jeudi soir est égale à :
P1 = 20% x 30% = 6%
b) La probabilité qu'il pleuve Jeudi après-midi et Vendredi Matin est égale à :
P2 = 20% x 70% = 14%
c) La probabilité qu'il pleuve Jeudi après-midi ou Vendredi Matin est égale à :
P3 = 20% + 70% - P2 = 20% + 70% - 14% =76%
d) La probabilité de n'avoir aucune goutte de pluie pendant ce temps est égale à :
P4 = 80% x 70% x 30% x 30% = 5%
e) La probabilité qu'il pleuve au moins une fois pendant cette période de 24 heures est égale à :
100% - P(qu'il ne pleuve pas du tout) =
P5 = 100% - (80% x 70% x 30% x 30%) = 100% - 5% = 95%
e) La probabilité qu'il pleuve au plus une fois ces 24 heures.
C'est à dire 1 ou moins:
Cette probabilité est égale à:
P6 = P4 +
80% x 70% x 30% x 70% +
80% x 70% x 70% x 30% +
80% x 30% x 30% x 30% +
20% x 70% x 30% x 30%
=
5% + 11,76% + 11,76% + 2.16% + 1.26% =
31.94%
Exercice 18
Question:
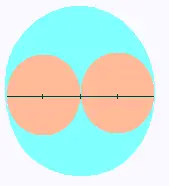
Un programme informatique génère des points
au hasard à l'interieur du grand cercle.
a)Quelle est la probabilité de l'événement élémentaire C1: "un des points se situe à l'intérieur de l'un des petits cercles"?
b)Quelle est la probabilité de l'événement C2: "un des points se
situe à l'intérieur des deux petits cercles"?
c)Quelle est la probabilité de l'événement complémentaire de l'événement C2?
Réponse:
a) P(C1) = πr2/π(2r)r2 = 1/4.
b) P(C2) = (πr2 + πr2)/π(2r)r2 = 2πr2/4πr2 = 1/2
c) P(complémentaire de C2) = 1 - P(C2) =
1 - 1/2 = 1/2
Exercice 19
Question:
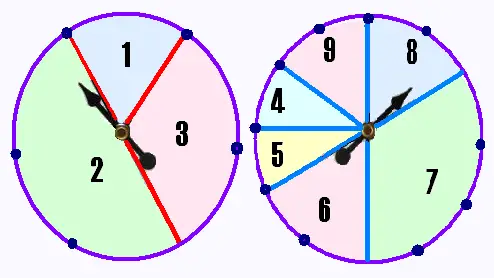
On fait tourner deux roulettes et on note le nombre formé par les chiffres obtenus sur chacune d'elles.
La première roulette donne le chiffre des dizaines
et la deuxième le chiffre des unités.
Les points sur les cercles déterminent des arcs
isométriques sur chacune des roulettes.
a) Quelle est la probobilité d'obtenir le nombre 27 ?
b) Peut-on former des combinaisons de chiffres dans
cette expérience aléatoire? Justifier la réponse.
c) Combien de nombres peut-on former dans
cette expérience aléatoire?
Réponse:
a) P(27) = (3/6) x (7/12) = 29.17%.
b) On ne peut pas former des combinaisons.
Tout les nombres obtenus sans différents et déjà
ordonnés.
c) On peut former n x p = 3 x 6 = 18 nombres.
n = 3 est le nombre de secteurs de la première roulette,
et
p = 6 est le nombre de secteurs de la deuxième roulette.
Exercice 20
Question:

On effectue un sondage auprès de 500 familles de
trois enfants et plus sur la marque
des téléphones intelligents (TI) qu'ils utilisent.
Nous avons le tableau suivant:
| Marque des TI | Pourcentage |
| iPhone | 50 |
| Samsung | 56 |
| Motorola | 30 |
| BlackBerry | 45 |
| Sony | 18 |
| LG Marquee | 12 |
| Autres | 7 |
(Ce tableau est fictif)
a) La somme des pourcentages donne-t-elle 100% ?
b) On choisie une famille au hasard parmi les 500
qui ont été intérrogées. Quelle est la probabilité
qu'elle n'utilise pas un BlackBerry?
Réponse:
a) La somme des probabilités de donnerait pas 100%
puisque les événements associés à chacun des pourcentages
ne sont incompatibles.
En effet, parmi ces évenements, il y a ceux qui
possèdent des résultas communs. Une famille de trois enfants et plus peut bien avoir, au plus, trois
téléphones intélligents.
b) Parmi les 500 familles intérrogées, 45% utilsent
un BlackBerry. Donc 55% des familles ne l'utilisent pas.
La probabilité qu'une famille prise au hasard, n'utilise pas un BlackBerry est égale à 55%.
|