probabilités géométriques
probabilités brevet
Mathématiques 2: Probabilités géométriques
1. Variable continue et discontinue
1. Variable continue
Lorsqu'on lance un dé à 6 faces et on note les nombres impairs
qui sortent. "Obtenir un résultat impair" est un événement
discret.
Une variable est dite disctète si on peut
en dénombrer les résultats.
La variable aléatoire X : (obtenir un résultat impair) est une
variable discrète car on peut en dénombrer les résultats, qui
sont {1, 3, 5}.
La probabilité correspondante est égale à:
(nombre de cas favorables)/(nombre de cas possibles) = 3/6 = 1/2.
2. Variable discontinue

Une variable est dite continue si on ne peut pas
en dénombrer les résultats.
Si on choisit au hasard un point sur le segment AD.
Quelle est la probabilité que ce point se situe sur le
segment BC ?
Ici, on ne peut pas dénombrer les cas favorables et les
cas possibles, car il en existe une infinité.
La variable aléatoire X : (un point sur le segement [BC]) :
est une variable continue car elle prend une infinité
et non dénombrable valeurs.
Das ce genre de situations, on fait appel aux
probabilités géométriques.
2. Définition
Le calcul des probabilités ne se limite pas au tirage
au sort avec un dénombrement. Il inclu également les chances relatives aux
endroits dans l'espace, qui
nécessitant des mesures et font donc appel à
la géométrie. Les probabilités correspondantes sont
dites probabilités géométriques.
La probabilité mesurée sera donc un rapport
de mesure de longueurs, de mesures d’angles, de périmètres,
d’aires, ou de volumes. Ainsi la probabilité géométrique
implique des calculs aussi bien dans l'espace à une
dimension que l'espace à deux ou à trois dimensions.
Dans la plus part des cas, comme dans les exemples qui
suivent, on considère toujours que les événements
d’atteindre un endroit dans l'espace sont équiprobables.
3. Exemples
1. Probabilité à une dimension:
Présence sur une longeur
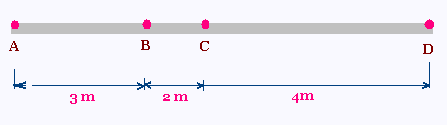
On choisit au hasard un point sur le segment AD.
Quelle est la probabilité que ce point se trouve
sur le segment [BC] ?
Il s'agit d'un calcul de probabilité géométrique à
une dimension.
Cette probabilité est égale à
P(sur le segment[BC]) = mes[BC]/mes[AD] = 2cm/9cm = 2/9.
2. Probabilité à deux dimensions
Présence sur une surface: jeu de flechette
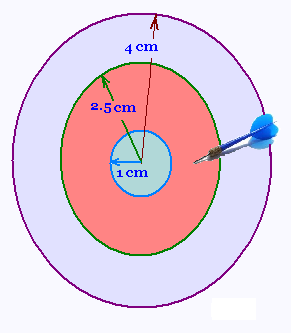
On considère une cible circulaire de rayon 4 cm divisée en 3
zones annulaires séparées par des cercles concentriques
de rayon 1 cm et 2.5 cm.
Au lancer de la fléchette, on veut savoir la probabilité que
le joueur touche la cible dans la zone annulaire rouge
comprise entre les cercles de rayons 1 cm et 2.5 cm.
La probabilité P(zone) que le fléchette touche cette zone
annulaire est:
P(zone) = l'aire de cette zone/l'aire totale du disque.
L'aire de la zone = π(2.5)2 - π(1)2 =
π(6.25 - 1) = 5.25 π
L'aire totale du disque est π(4)2 = 16 π
Ainsi
P(zone) = 5.25π/16π = 5.25/16 = 0.33 = 33%.
3. Probabilité à trois dimensions
Balle dans une cavité sphérique
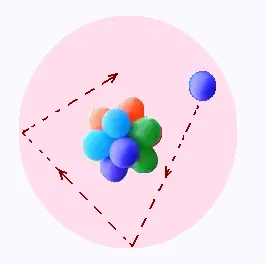
Une balle rebondit dans une cavité sphérique comprenant
8 autres balles collées ensemble. Toutes ses balles ont
un même volume. Le volume de la cavité est 40 fois
plus grand que le volume d'une balle.
Quelle est la probabilité de présence de la balle
rebondissante dans l'espace qui lui est offert?
Volume de la balle = Vb
Volume de la cavité sphérique = Vc = 40 x Vb
Volume des 8 autres collées ensemble = V8 = 8 x Vb
Le volume de l'espace restant qui est offert à la balle
rebondissante est: Vr = Vc - V8 = 40 Vb - 8 Vb = 32 Vb
La probabilité de trouver la balle rebondissante
dans cet espace libre est donc:
P(balle) = Volume de la balle/l'espce qui lui est offert =
Vb/32Vb = 1/32 = 0.03 = 3%
4. Probabilité à deux dimensions
La méthode de Monte-Carlo
4.1. Description
La méthode Monte-Carlo est couramment utilisée en mathématiques et en physique des particules.
Le nom de cette méthode fait allusion aux jeux de hasard pratiqués à Monte-Carlo. Elle a été inventé en 1947 par Nicholas Metropolis.
Cette technique a pour but de founir des résultats
probabilistes. Ces résultats sont approximatifs en raison des probabilités utilisées dans les calculs.
Elle consiste à trouver un modèle qui conduirait au résultat attendu, générer des nombres aléatoires, faire des itérations, et enfin donner le résultat.
4.2. Exemple: Calcul du nombre π
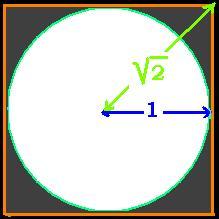
Dans cet exemple, on veut trouver la valeur du nombre π.
Cette technique consiste ici à:
- Modèle: Utiliser un carré et un cercle,
- Générer de nombres aléatoires sur le quart du cercle
et sur le quart du carré, (nombres aléatoires = nombres au hasard = random numbers)
- Faire le rapport de ses nombres,
- Trouver la valeur approximative du nombre π.
La zone qui correspond au quart de la surface du carré, et
dont l'aire vaut As = 1/4, sera atteinte par Ns nombres aléatoires.
La zone qui correspond au quart de la surface du cercle, et
dont l'aire vaut Ac = π/4, sera atteinte par Nc nombres aléatoires.
Ainsi le rapport des aires des surfaces est égal au rapport des
nombres aléatoires qui ont atteint les deux surfaces.
C'est à dire:
Ac/As = Nc/Ns = π
Ce qui donne une valeure approximative du nombre π.
Plus on génére des nombres, plus le résultat est précis.
4.3. Programme relatif
Ce programme en php utilise la méthode Monte-Carlo
pour donner une valeur approximative du nombre π.
Le nombre d'itérations est fixé à 100 000.
Pour une telle même valeur, le résultat donnée
fluctue puisque les nombres alétoires générés
fluctuent (appyer plusieurs fois sur le bouton pi).
|