Mathématiques
2
Problèmes CD
© The scientific sentence. 2010
|
Mathématiques: Géométrie
Théorème d'Archimède
1. Archimède

Archimède de Syracuse est un mathématicien, physicien et ingénieur
de la Grèce antique. Il est l'un des principaux scientifiques de
l'Antiquité. Il est né à Syracuse vers - 287 et mort à Syracuse
en - 212.
Syracuse est une ville italienne située
sur la côte, au sud-est de la Sicile. Elle fut fondée au
8e siècle av. J.C. par des colons grecs.
Les Romains, sous les ordres du général Claudius Marcellus,
ont conqui Syracuse en - 212.
Peu avant sa mort,
Archimède a demandé qu'une gravure d'une sphère inscrtite
dans un cylindre soit faite sur sa pierre tombale.
Cette pierre tombale était encore visible à l’époque de Cicéron
qui la redécouvrit deux siècles plus tard. Cicéron (Marcus
Tullius Cicero: - 106: - 43) est un philosophe et homme d'état
romain qui vivait à l'époque de Jules César.
Le tombeau d'Archimède est tombé dans l'oubli à nouveau,
et sans doute n'existe plus.
Archimède a écrit plusieurs traités, dont quelques uns ont été perdus.
L'un de ces traités est intitulé
De la sphère et du cylindre, en deux livres: livres I et livre II.
2. Théorème Archimède
De la sphère et du cylindre est l'œuvre d'Archimède qui
décrit comment calculer l'aire et le volume d'une boule
et d'un cylindre.
Dans ce traité, Archimède montre que l'aire d'un cylindre est :
A = 2 πr2 + 2 π r h = 2 π r (r + h).
et que son volume est :
V = πr2 h.
Il montre aussi que l'aire d'une sphère est égale à quatre
fois l'aire du disque délimité par son grand cercle. En mathématiques modernes, l'aire de la sphère est égale 4 πr2 et l'aire du disque est égale à πr2.
Il montre que le volume Vs de la sphère est égal aux deux-tiers du volume Vc du cylindre circonscrit à cette sphère.
Vs = (4/3) πr3
Vc = πr2 x 2 r = 2 πr3
D'où:
Vs/Vc = 2/3
Archimède est si fier de ce dernier résultat qu'il demande que soit gravé sur sa tombe le dessin d'une sphère inscrite dans un cylindre.
Nous avons aussi:
Aire de la sphère: As = 4 πr2
Aire du cylindre: Ac = 2 π r (r + h) = 2 π r (r + 2r) = 6 πr2
D'où:
As/Ac = 2/3
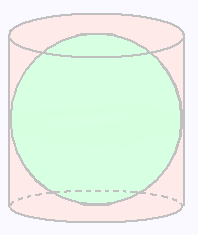
Que se soit l'aire totale ou le volume, le rapport
est toujours égal à 2/3.
Théorème d'Archimède:
Une sphere est les deux tiers du cylindre qui lui est circonscrit.
|
|