Mathématiques
Problèmes du
second degré
Rappels
Problèmes - Brevet
Problèmes du sd degré
Calculateurs
© The scientific sentence. 2010
|
Mathématiques: Fonction quadratique
Carré inscrit dans un autre carré
1. Cas particulier
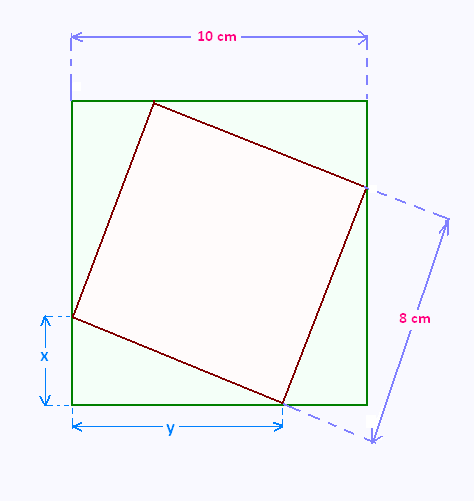
Dans un carré de 100 cm2, on veut inscrire un
deuxième carré de 64 cm2.
Quelles sont alors les positions des sommets de ce
petit triangle ?
Réponse
On calcule donc x et y.
D'après la propriété de Pythagore, nous avons
x2 + y2 = 82 = 64 (1)
De plus, d'après la symétrie du problème
x + y = 10 (2)
(2) donne y = 10 - x .
On substitue cette dernière relation dans (1) et on trouve:
x2 + (10 - x)2 = 64
On développe et on réduit:
2x2 + 100 - 20x = 64
2x2 - 20x + 36 = 0
x2 - 10x + 18 = 0
Discriminant réduit Δ' = 25 - (1)(18) = 7
La solution est donc :
x = 5 - √7
et
y = 5 + √7
2. Cas général
Dans le cas général où le côté du grand carré est a
et le côté du carré inscrit est b, on aura:
x + y = a (G1)
x2 + y2 = b2 (G2)
On substituant (G1) dans (G2), on obtient :
x2 + (a - x)2 = b2
On développe, et on obtient l'équation associée
à une fonction quadratique, c'est à dire une équation
du deuxième degré à une inconnue associée au trinôme
x2 + (a - x)2 - b2.
2 x2 - 2 a x + a2 = b2
2 x2 - 2 a x + a2 - b2 = 0
Δ' = (- a)2 - (2) (a2 - b2) =
a2 - 2a2 + 2 b2 = 2 b2 - a2
Les solutions sont:
x = (a ± √(2 b2 - a2))/2
Les dimensions géométriques sont positives,
nous avons donc a ≥ 0 et b ≥ 0.
• Pour avoir une solution positive, on doit avoir :
a ≥ √(2 b2 - a2)
a2 ≥ 2 b2 - a2
a2 ≥ b2
a ≥ b
Les dimensions géométriques sont réelles.
• Pour avoir une solution réelle, on doit avoir
un discriminat positif, donc:
2 b2 - a2 ≥ 0
b2 ≥ a2/2
b ≥ a/√2
On peut représenter a/√2, b et a sur une
droite graduée:
0 ------ a/√2 -------- b ---------- a
On note bien que x ne peut prendre que les valeurs de 0 à a
et que y ne peut prendre que les valeurs de a à 0, ou
inversement.
Exemple:
Si a = 10 cm, alors a/√2 = 7.07 cm .
Les seules valeurs que peut prendre b sont
comprises entre 7.07 et 10.
|
|