Mathématiques
Problèmes du
second degré
Rappels
Problèmes - Brevet
Problèmes du sd degré
Calculateurs
© The scientific sentence. 2010
|
Mathématiques 34: Algèbre
Fonction quadratique
Intersection d'une parabole avec
des droites
1 . Points d'intersection
d'une parabole et d'une droite
On dispose de deux méthodes our trouver les pionts d'intersection
d'une parabole et d'une droite: la méthode algébrique et la
méthode graphique.
1.1. Méthode algébrique
La méthode algébrique est rigoureuse. Elle est
basée sur des calculs.
Pour definir les points d'intersection
d'une parabole et d'une droite, on
égalise leurs définitions respectives.
C'est à dire si :
yp = ax 2 + b x + c
est la définition de la fonction quadratique et
yd = α x + β
est la définition de la droite affine,
alors
leurs points d'intersection obéissent à l'égalité:
yp = yd
.
Donc
ax 2 + b x + c = α x + β
On réduit et on on obtient :
ax 2 + b x + c - α x - β = 0
ax 2 + (b - α) x + c - β = 0
On obtient donc une équation quadratique des points
d'intersection, à résoudre.
ax 2 + (b - α) x + c - β = 0
Si ses solutions sont s1 et s2, on calcule leurs
ordonnées repectives par l'une ou l'autre des
deux expressions égalisées yp ou
yd. On choisi la plus simple,
c'est à dire yd = α x + β.
Ainsi,
l'ordonnée de s1 est ys1 = α s1 + β.
Celle de s2 est ys2 = α s2 + β
Les deux points d'intersection sont donc:
P1 (s1, ys1)
et
P2 (s2, ys2)
On note alors ces deux points sur le graphe.
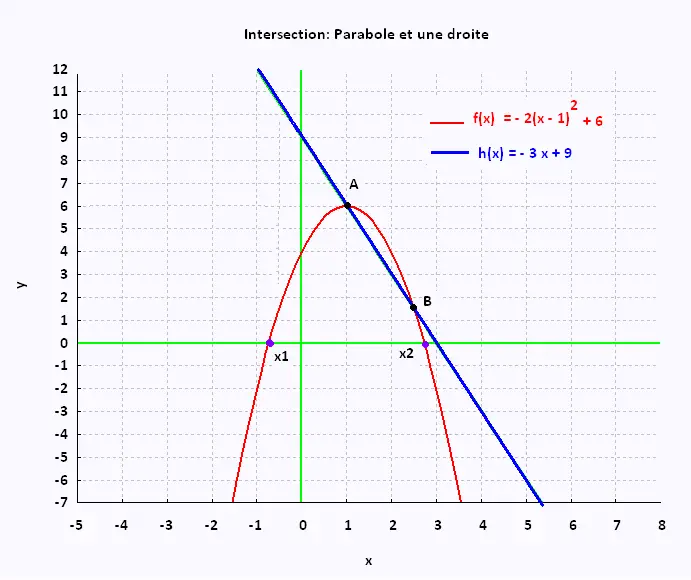
Exemple:
P: y = - 2(x - 1)2 + 6 , et
D: y = - 3x + 9
On doit ecrire la fonction quadratique sous sa forme
générale. Il suffit de développer:
- 2(x - 1)+ 6 = - 2(x - 2 x + 1) + 6 =
- 2x2 + 4 x - 2 + 6 = - 2x2 + 4 x + 4
On a donc :
yp = - 2x + 4 x + 4
yd = - 3x + 9
On égalise:
- 2x2 + 4 x + 4 = - 3x + 9
On réduit et on obtient:
- 2x2 + 7 x - 5 = 0
On résout cette équation du second degré:
Δ = (7)2 - 4(- 2)(- 5) = 49 - 40 = 9
√Δ = 3
Les racines de cette équation sont donc :
s1 = (- 7 + 3)/2(- 2) = + 1
s1 = (- 7 - 3)/2(- 2) = 5/2 = 2.5
s1 = + 1 et
s2 = + 5/2
On calcule leur ordonnées:
l'ordonnée de s1 est ys1 = - 3(1)+ 9 = + 6.
Celle de s2 est ys2 = - 3(5/2)+ 9 = (- 15 + 18)/2 = 3/2 = 1.5
Les points d'intersection sont alors:
A (+1,+6) et
B(5/2, 3/2)
On retrouve ces points sur le graphique.
1.2. Méthode graphique
• La méthode graphique donne les points d'intersection,
mais ce n'est pas très rigoureux , car elle nécessite des
précisions sur les lectures.
Pour cela, il suffit de tracer le graphe de la parabole, puis
le graphe de la droite et de noter les abscicces et
les ordonnées des points intersections, s'ils existent.
Exemple:
P: y = - 2(x - 1)2 + 6 , et
D: y = - 3x + 9
On trace les graphes de la fonction quadratique
et de la fonction affine:
• La parabole a pour extremum le point (h, k),
c'est à dire le point (1, 6).
La parabole a pour a = - 2, donc négative. Elle est
donc ouverte vers le bas.
Les zéros de la fonction quadratique se calcule en
posant:
- 2(x - 1)2 + 6 = 0
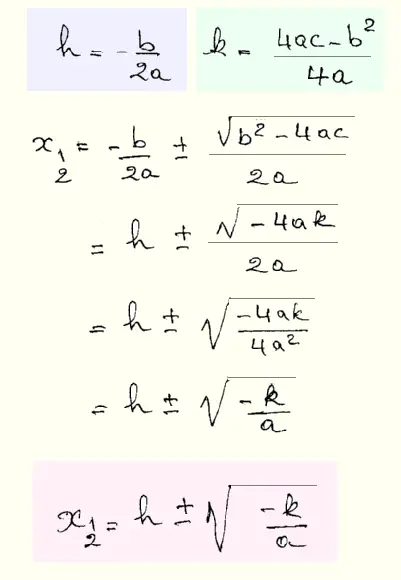 > >
On trouve
r1 = 1 + √((- 6)/(- 2)) = 1 + √3 = 2.73
r2 = 1 - √((- 6)/(- 2)) = 1 - √3 = - 0.73
On place les points correspondants sur
le graphique.
On trace alors la courbe de la fonction quadratique qui est une
parabole:
. remontant de - ∞ ,
. passant par x2 = - 0.73 ,
. remontant jusqu'au maximum (1,6),
. descendant en coupant l'axe des x en x1 = 2.73, et puis
. continuant à descendr vers - ∞ .
• Pour tracer la droite affine, il
suffit de deux poits. On choisi les points les
plus simples:
y = - 3x + 9
x = 0 → y = 9 (ordonné à l'origine)
y = 0 → - 3x + 9 = 0 → x = 3 (abscisse à l'origine) .
On trace la droite passant par ces deux points.
À partir du graphe, on note les points d'intersection de la
prabole et de la droite affine.
2 . Parabole et une droite :
Deux points d'intersection
Si
yp = ax 2 + b x + c
est la définition de la fonction quadratique et
yd1 = α x + β
est la définition de la première droite affine, et
yd2 = α x + β
est la définition de la deuxième droite affine .
On procède de la même manière que pour l'intersection d'une
parabole avec une droite. Mais ici , on doit le faire deux fois:
La parabole avec la première droite affine, puis la parabole avec
la deuxième droite affine.
Ce type de problè n'a d'intérêt que si la parabole et
les deux droites ont toutes les trois un point commun.
Dans ce cas:
Si on sait qu'il ya un point commun à la parabole et
aux deux droites, on determine le point d'intersection de
la parabole avec une droite affine, puis, c'est plus simple,
le point des deux droites affines. Par transitivité, ce point
d'intersection est aussi celui de la parabole avec l'autre
droite.
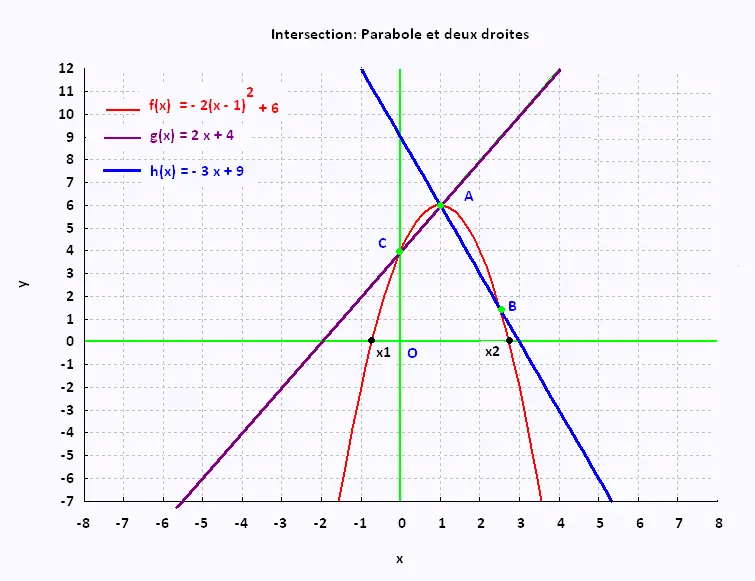
Exemple:
P: y = - 2(x - 1)2 + 6 ,
D1: y = 2x + 4 , et
D2: y = - 3x + 9
3. Cas particuliers
1. Un seul point d'intersection:
Si l'équation des points d'intersection:
ax 2 + (b - α) x + c - β = 0
admet un discriminant nul, alors il un seul
point
d'intersection entre la parabole et la droite sffine.
Exemples :
Exemple 1 :
P: y = - 2(x - 1)2 + 6 ,
D: y = 6
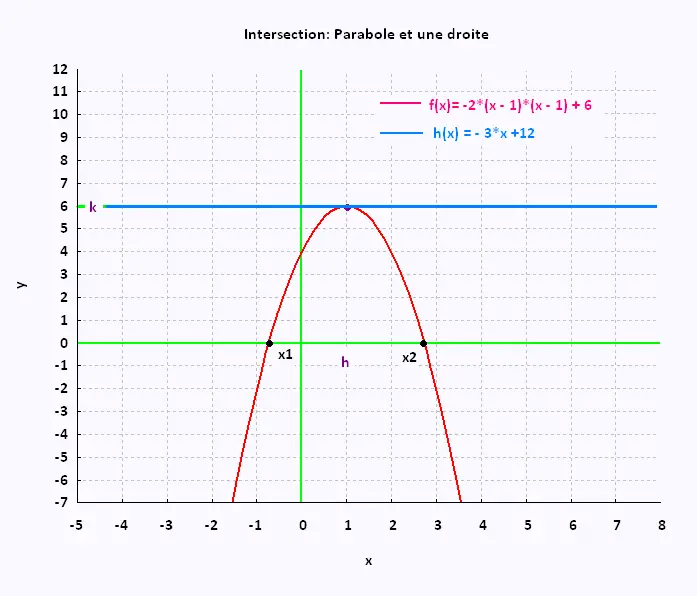
Le seul point commun est P(1,6). La droite est parallèle
à l'axe des x.
Exemple 2:
P: y = - 2(x - 1)2 + 6 ,
D: y = - 4x + 12
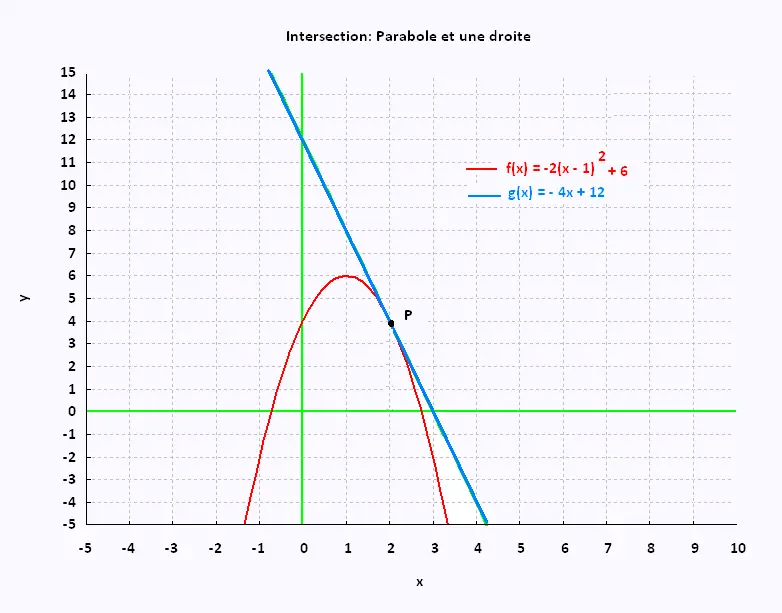
La seul point commun est P(2,4) . La droite est tangente
à la parabole, au point P .
2. Aucun point d'intersection:
Si l'équation des points d'intersection:
ax 2 + (b - α) x + c - β = 0
admet un discriminant négatif, alors il n'existe aucun
point d'intersection entre la parabole et la droite sffine.
Exemples :
Exemple 1:
P: y = - 2(x - 1)2 + 6
D: y = 9
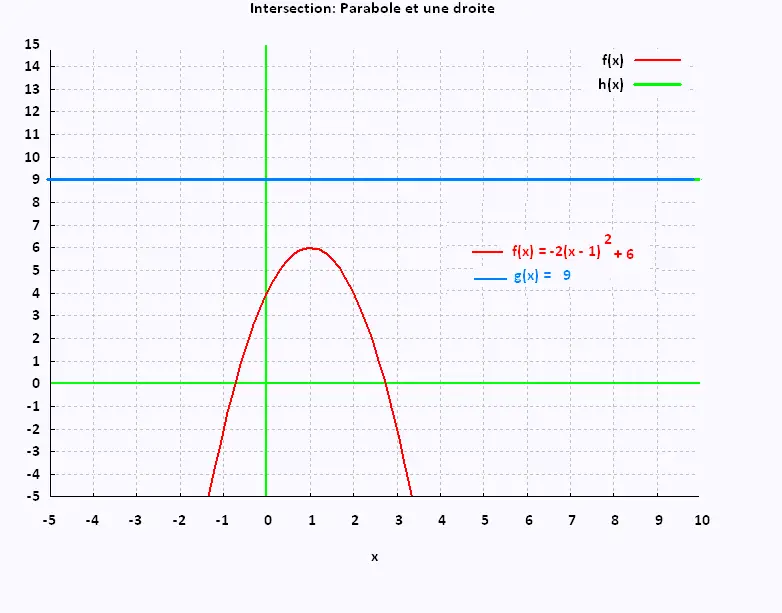
Exemple 2:
P: y = - 2(x - 1)2 + 6
D: y = - 4x + 16
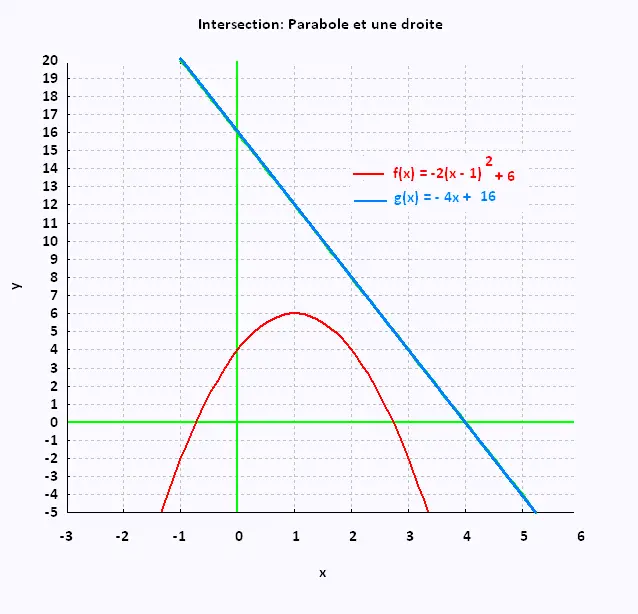
4 . Application: Déterminer l'aire du
triangle engendré sous la parabole
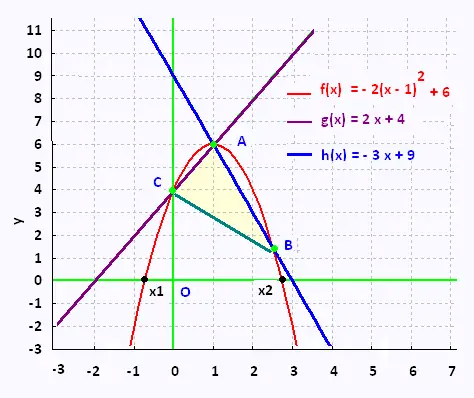
Nous savons que:
A(1,6), B(5/2, 3/2) et C(0.4) . D'où:
Calculons les trois distances entre les trois points
A, B et C:
• D(A,B) = √[(5/2 - 1)2 + (3/2 - 6)2] =
√[(3/2)2 + (- 9/2)2] =
√(9/4 + 81/4) = √(45/2) = 3 √(5/2) =
4.74 unités.
• D(B, C) = √[(0 - 5/2)2 + (4 - 3/2)2] =
√[(- 5/2)2 + (5/2)2] =
√(25/4 + 25/4) = √ (25/2) = (5/2) √2 =
3.53 unités.
• D(C, A) = √[(0 - 1)2 + (4 - 6)2] =
√( 1 + 4) = √5 =
2.24 unités.
• Demi-périmètre = [3 √(5/2) + (5/2) √2 + √5]/2
= 5.26
La formule de Héron donne l'aire du triangle ABC:
• Aire = √[5.26 (5.26 - 4.74) (5.26- 3.53) (5.26 - 2.24)]
3.80 unités carrées.
L'aire du triangle ABC est égale à 3.80 unités carrées.
|
|