Mathématiques
Problèmes du
second degré
Rappels
Problèmes - Brevet
Problèmes du sd degré
Calculateurs
© The scientific sentence. 2010
|
Algèbre : fonction quadratique
pigeon d’argile
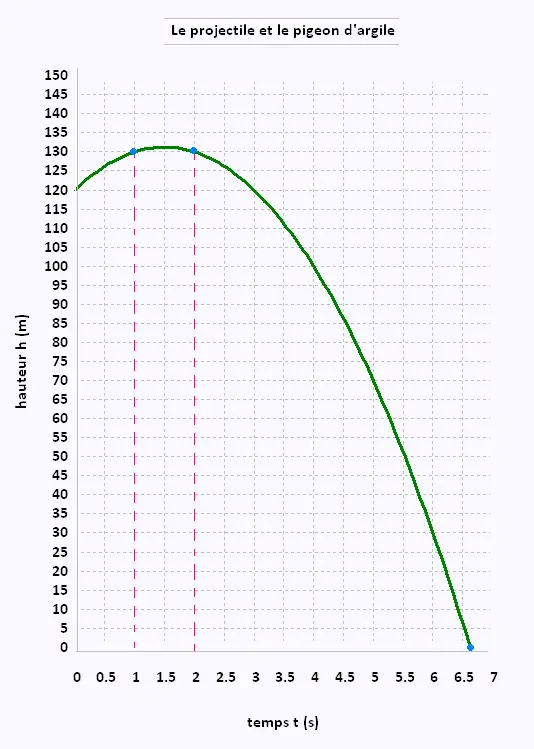
Du haut d’une falaise, à 120 m au-dessus du niveau de la mer,
un appareil lance dans les airs un pigeon d’argile. On peut
représenter sa hauteur h(t) (en m) par rapport au niveau de la
mer selon le temps t écoulé (en s) depuis le lancement par
l’équation
h(t) = 120 + 15t - 5t2
a) Après combien de temps le pigeon d’argile :
1) Aura-t-il atteint sa hauteur maximale?
2) Aura-t-il atteint la mer ?
b) Le projectile d’un tireur atteint le pigeon d’argile
à une hauteur de 130 m. Combien de temps
après le lancement le pigeon a-t-il été atteint?
1)
h(t) = - 5[(t2 – 3 t + 9/4) – 9/4 – 24]
h(t) = - 5[(t2 – 2 (3/2) t + 9/4) – 9/4 – 24]
h(t) = - 5[(t – 3/2)2 – 105/4]
h(t) = - 5(t – 3/2)2 + 525/4
h = 3/2 , k = 525/4
L'abscisse du sommet est t = 3/2 = 1.5
Le projectile aura atteint sa hauteur maximale après 1.5 s.
2)
Au niveau de la mer, h(t) = 0
On cherche donc les zéros de la fonction:
h(t) = 120 + 15t - 5t2 = 0
120 + 15t - 5t2 = 0
- 5t2 + 15t + 120 = 0
- 5(t2 - 3 t - 24) = 0
t2 - 3 t - 24 = 0
a = 1, b = - 3 , c = - 24
Le projectile aura atteint la mer à 6.6 s.
b)
Àune hauteur de 130 m, on aura:
h(t) = 120 + 15t - 5t2 = 130
120 + 15t - 5t2 - 130 = 0
- 5t2 + 15t - 10 = 0
- 5(t2 - 3 t + 2) = 0
t2 - 3 t + 2 = 0
a = 1, b = - 3 , c = 2
À une hauteur de 130 m, le pigeon a été atteint
soit à 1 s, soit à 2 s, après le lancement du
projectile.
|
|