Mathématiques
Problèmes du
second degré
Rappels
Problèmes - Brevet
Problèmes du sd degré
Calculateurs
© The scientific sentence. 2010
| Mathématiques 2: Fonction quadratique &
distance dans le plan cartésien
Exercice 1
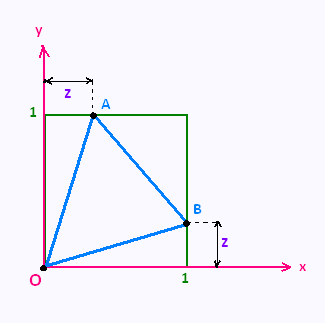
On inscrit un triangle équilatéral OAB dans un carré
de côté égal à 1.
a) Calcul de la valeur du côté du triangle:
Le triangle OAB est équilatéral donc les trois
segments [OA], [OB], et [AB] sont isométriques.
Les distances d(O,A) = d(O,B) sont égales et ne
dépendent que de 1 et de z, donc z est le même.
Le poit O a pour coordonnées (0,0),
Le point A a pour coordonnées (z,1), et
Le point B a pour coordonnées (1,z),
Nous avons
d(O,A) = √(z2 + 12)
d(O,B) = √(12 + z2)
d(A,B) = √((1 - z)2 + (z - 1)2) =
√(2(1 - z)2)
La condition d(O,A) = d(O,B) = d(A,B) implique:
√(z2 + 12) = √(2(1 - z)2)
En élevant au carré les deux membres de cette égalité, on
obtient:
z2 + 12 = 2(1 - z)2
On développe le deuxième membre de l'égalité:
z2 + 12 = 2(1 - 2 z + z2) =
2 - 4 z + 2z2
On réduit, et on obtient:
z2 - 4 z + 1 = 0
Δ = (- 4)2 - 4 (1)(1) = 12 . Donc √Δ = 2√3
z1 = (4 + √12)/2 = (4 + 2√3)/2 = 2 + √3 = 3.732
z2 = (4 - √12)/2 = (4 - 2√3)/2 = 2 - √3 = 0.268
Les valeurs des carrés des côtés sont :
1 + z12 = 4(2 + √3) = 14.928
1 + z22 = 4(2 - √3) = 1.072
Les valeurs des côtés sont donc:
√(1 + z12) = 2 √((2 + √3)) = 3.864
√(1 + z22) = 2 √((2 - √3))) = 1.035
La valeur 3.86 du côté qui correspond à la racine la plus grande
z1 est plus grande que 1. Elle ne correspond pas au contexte.
On retient la deuxième racine:
d(O,A) = d(O,B) = d(A,B) = √(1 + z22) =
√(4(2 - √3)) = 2 √(2 - √3) = 1.035
d(O,A) = d(O,B) = d(A,B) = 2 √(2 - √3) = 1.035 unités
b) Calcul de l'aire du triangle:
Dans un triangle équilatéral, une hauteur est
en même temps médiane.
L'aire d'un triangle est égale à base x hauteur/2
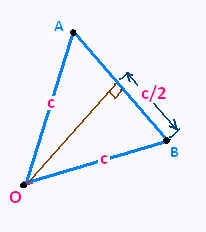
Dans le triangle équilatéral OAB, de côté c = 2 √(2 - √3), nous avons:
hauteur = √(c2 - (c/2)2) =
√(3c2/4) = (c/2)√3
L'aire A = c x (c/2)√3 /2 =
√3 c2/4 =
(2 √(2 - √3))2 √3 /4 =
4(2 - √3) √3 /4 = (2 - √3) √3 =
2√3 - 3
Aire du triangle OAB = 2√3 - 3 = 0.464 unités2
Exercice 2
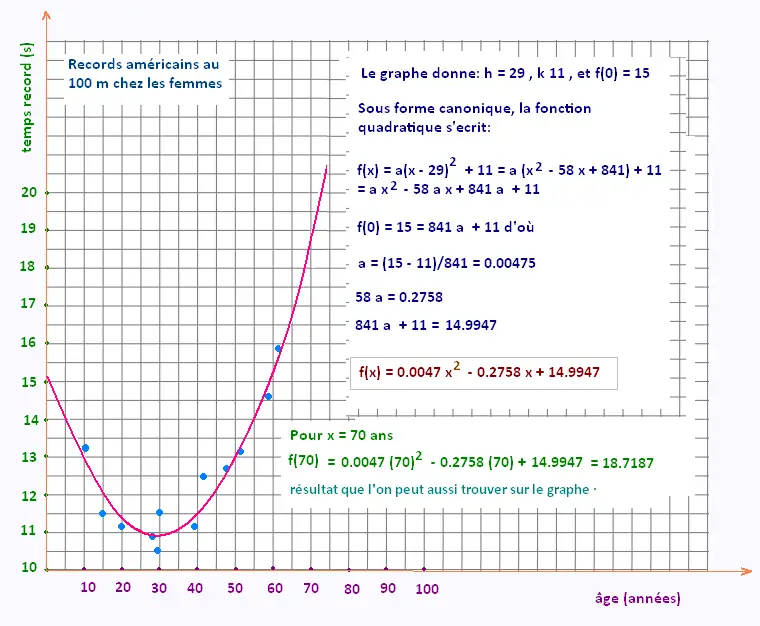
Utiliser le logiciel pour vérifier :
Entrer les valeurs:
10,15,20,27,29,30,38,42,47,51,58,61
13.2,11.5,11.2,10.9,10.5,11.5,11.2,12.5,12.7,13.1,14.6,15.8
 Régression quadratique ScientificSentence Régression quadratique ScientificSentence
On peut aussi utilser une calculette pour faire
la régression quadratique.
Pour l'exemple de la calculette casio :
 Régression quadratique casio Régression quadratique casio
Exercice 3
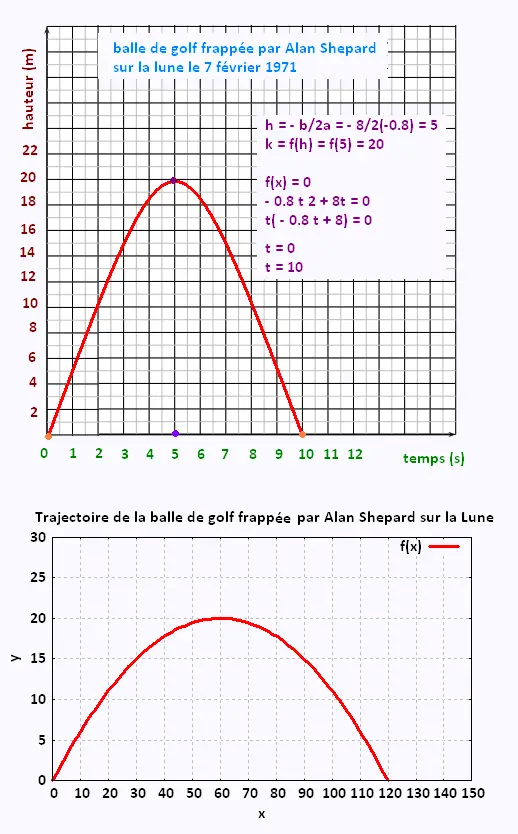
a) Voir grahique
b) Les zéros de la fonction sont :
t = 0 et t = 10.
t = 0 représente le moment où Alan Shepard a frappé la balle,
t = 10 représente le moment où la balle a touché le sol.
c)
x : le déplacement horizontal de la balle (en m),
y : la hauteur de la balle (en m)
x = 12 t d'où t = x/12
On substitue cette valeur de t dans l'équation
y = - 0.8 t2 + 8 t , on
obtient:
y = - 0.8 (x/12)2 + 8 (x/12) =
- 0.8 (x2 /144) + (8/12) x =
- (1/180) x2 + (2/3) x
y = - (1/180) x2 + (2/3) x
d) voir graphique
e)
f(x) = 0
- (1/180) x2 + (2/3) x = 0
x (- (1/180) x + (2/3) ) = 0
d'où
x = 0
x = (2/3)/(1/180) = 180 (2/3) = 120
x = 0 est le lieu où l'astronaute a lancé la balle
x = 120 m, le lieu où la balle a touché le sol lunaire.
Exercice 4
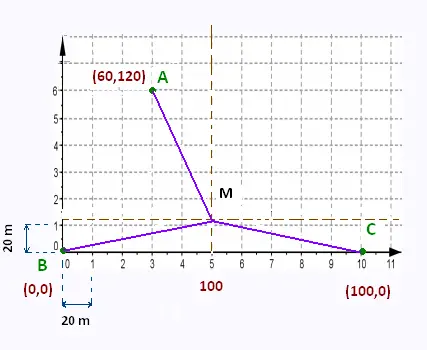
Soient trois points B(0,0), C(0,200), et
A(60,120).
Quel est la position d'un nouveau point M(x,y) équidisatnt des
trois point ?
La position de B est prise pour origine
du plan cartésien:.
La distance entre le pont B et le point C
est de 200 m.
Le nouveau point M(x,y) sera situé à égale distance
du point B et du point C, il va se trouver
sur la droite d’équation x = 100. Il aura donc
pur coordonnées (100, y).
De plus, ce nouveau point sera situé à égale
distance du point B d'une part et du point C d'autre part.
Ainsi, on aura:
d(A,M) = √((60 - 100)2 + (120 - y)2) =
√(402 + (120 - y)2)
d(B,M) = √((0 - 100)2 + (0 - y)2) =
√(1002 + y2)
d(A,M) = d(B,M) implique:
√(402 + (120 - y)2) = √(1002 + y2)
En élevant au carré les membres de cette équation, on trouve:
402 + 1202 - 240 y + y2 = 1002 + y2
402 + 1202 - 1002 = 240 y
240 y = 1600 + 14400 - 10000 = 6000
240 y = 6000/240 = 25
y = 25
Le nouveau point aura pour coordonnées (100, 25).
Exercice 5
Soit A(3,5) et B(6,x).
Quelle est la valeur de x pour que d(A,B) = 5
On doit résoudre l'équation:
(3 -6)2 + (5 - x)2 = 25
Réduite, cette équation devient:
x2 - 10 x + 9 = 0
Δ = (- 10)2 - 4(1)(9) = 100 - 36 = 64
√Δ = 8
x1 = (10 + 8)/2 = 9
x2 = (10 - 8)/2 = 1
On trouve deux solutions : x = 1 ou x = 9 unités.
Exercice 6
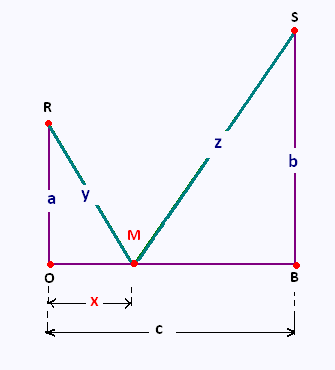
Soit deux points R(0,3) et S(10,5).
Quelle est la valeur minimale de la somme y + z ?
Application: a = 3 m, b = 5 m, et c = 10 m .
La formule de la distance permet d'ecrire:
y = √(a2 + x2)
z = √(b2 + (c - x)2)
a) 1er cas:
d(R,M) = d(S,M), c'est à dire y = z
√(a2 + x2) =
√(b2 + (c - x)2)
En élevant au carré, on obtient:
a2 + x2 =
b2 + (c - x)2
a2 + x2 =
b2 + c2 + x2 - 2 c x
a2 =
b2 + c2 - 2 c x
x = (b2 + c2 - a2)/2c
x = (52 + 102 - 32)/2x10 = 116/20 = 5.8 m
x = 5.8 m
b) y = z , donc L = y + z = 2y
y = √(32 + 5.82) = 6.53 m
L = y + z = 2 y = 13.06 m
L = y + z = 13.06 m
c) 2eme cas:
d(S,M) = 2 d(R,M), c'est à dire z = 2y
2 √(a2 + x2) =
√(b2 + (c - x)2)
En élevant au carré, on obtient:
4 a2 + 4 x2 =
b2 + c2 + x2 - 2 c x
3 x2 + 2 c x + 4 a2
- b2 - c2 = 0
3 x2 + 2 c x + 4 a2
- b2 - c2 = 0
Δ' = c2 - 3(4 a2
- b2 - c2) =
c2 - 12 a2
+3 b2 + 3 c2 =
4 c2 + 3 b2 - 12 a2
Deux racines réelles:
x1 = (- c + √Δ)/3
x2 = (- c - √Δ)/3
Avec
Δ' = 4 c2 + 3 b2 - 12 a2
Δ' = 4 x 100 + 3 x 25 - 12x 9 = 367
x1 = (- 10 + 19.16)/3 = 3.05 m
x2 = (- 10 - 19.16)/3 = - 9.72 m (à gauche de l'origine).
d)
On trouve deux valeurs pour y, pour z, et
pour la somme des distances:
y1 = √(a2 + x12)
z1 = √(b2 + (10 - x1)2)
d1 = y1 + z1 = y1 + 2 y1 = 3 y1
y1 = √(32 + 3.052)
= 4.28 m
z1 = √(52 + (10 - 3.05)2)
= 8.56 m
d1 = y1 + z1 = 4.28 + 8.56 = 12.84 m
d1 = y1 + z1 = 12.84 m
y2 = √(a2 + x22)
z2 = √(b2 + (10 - x2)2)
d2 = y2 + z2 = = 3 y2
y2 = √(32 + 9.722) =
10.17 m
z2 = √(52 + (10 + 9.72)2)
20.32 m
d2 = y2 + z2 = 10.17 + 20.32 = 30.49 m
d2 = y2 + z2 = 30.49 m
e)
Cas général: Somme des distances minimale:
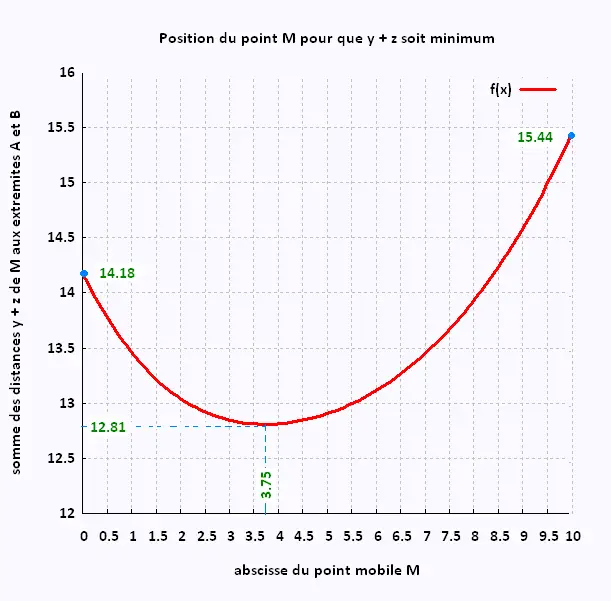
• première valeur de la distance L = y + z :
x = 0, donc L = 3 + √(102 + 52) = 14.18 m .
• dernière valeur de la distance L = y + z :
x = 10, donc L = 5 + √(102 + 32) = 15.44 m.
• Entre ces deux valeurs, nous avons un minimum x = 3.75 m
qui correspond à L = y + z =
√(3.752 + 32) + √((10 - 3.75)2 + 52) =
12.81 m .
La distance minimale d(A,M) + d(M,B) est égale à 12.81 m .
On peut trouver ce résultat algébriquement par un calcul de dérivée:
L = y + z = √(a2 + x2) + √((c - x)2 + b2)
dL/dx = (1/2) (2 x)/√(a2 + x2)
+ (1/2) (- 2 (c - x))/√((c - x)2 + b2)
= x /√(a2 + x2)
-(c - x))/√((c - x)2 + b2)
dL/dx = 0 =
x √((c - x)2 + b2) - (c - x) √(a2 + x2)
x √((c - x)2 + b2) = (c - x) √(a2 + x2)
En élevant au carré, on obtient:
x2 ((c - x)2 + b2) = (c - x)2 (a2 + x2)
(c - x)2 x2 + b2 x2 =
a2(c - x)2 + x2(c - x)2
b2 x2 = a2(c - x)2
b2 x2 = a2(c2 - 2 c x + x2)
b2 x2 = c2a2 - 2 ca2 x + x2a2
(b2 - a2) x2 + 2 c a2 x - c2a2 = 0
On résout l'équation et on trouve :
x = [- c a2 ± √(c2 a4 + (b2 - a2)c2a2)]/
(b2 - a2)
Application a = 3, b = 5 et c = 10
16 x2 + 180 x - 900 = 0
4 x2 + 45 x - 225 = 0
Δ = 5625 , √Δ = 75
x1 = (- 45 + 75) /8 = 3.75
x2 = (- 45 - 75) /8 = - 15
x1 = 3.75 m
x2 = - 15 m (15 m à gauche de l'origine). Cette solution ne
correspond pas au contexte considéré. On retient x = 3.75 m.
Exercice 7 : Pont de Sydney
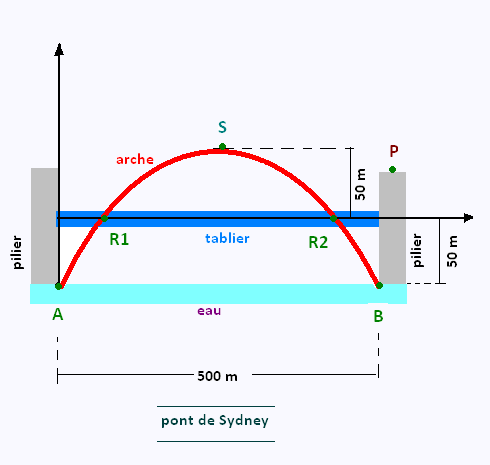
a)
Les coordonnées du sommet de l'arche sont
S(250,50)
Les coordonnées de l'extrémité gauche
de l'arche sont G(0,- 50)
Les coordonnées de l'extrémité droite
de l'arche sont G(500,- 50)
b)
L'équation de la parabole (arche)
est :
y = a (x - 250)2 + 50
y(0) = - 50 = a (0 - 250)2 + 50 =
a 2502 + 50
- 50 = a 2502 + 50
D'où:
a = - 100/2502 = - 1/625
y = - (1/625) (x - 250)2 + 50
c)
Les points de rencontre de l'arche et le tablier
sont les zéros de la fonction quadratique
f(x) = - (1/625) (x - 250)2 + 50.
- (1/625) (x - 250)2 + 50 = 0
(x - 250)2 - 50 /(1/625) = 0
(x - 250)2 - 50 x 625 = 0
(x - 250)2 - 2 252 52 = 0
Factorisée, l'équation devient:
(x - 250 - 125√2)(x - 250 + √2) = 0
d'où les solutions:
x = 250 + 125√2 = 426.77 m
x = 250 - 125√2 = 73.22 m
La distance entre ces deux points est
426.77 - 73.22 = 353.55 m
d) d(R1,A) = √((73.22 - 0)2 + (0 - 50)2) =
√(73.222 + (- 50)2) = 88.7 m
d(R2,B) = √((426.77 - 500)2 + (0 - 50)2) =
√(73.232 - (- 50)2) = 88.7 m
e)
S(250,50)
P(500, 90 - 50) = (500,40)
d(S,P) = √((500 - 250)2 + (50 - 40)2) =
√(2502 + 102) = 250.2 m
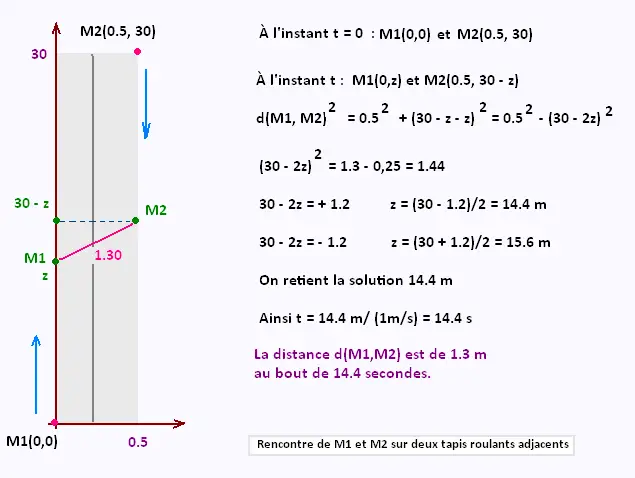
Exercice 8 : Deux tapis roulants adjacents
|
|