Mathématiques 2: Géométrie
Théorème de Pythagore
Autres applications
Mont Everest

1. Présentation

On veut estimer la longeur d'un téléphérique du Katmandou au Mont Everest au Népal.

Katmandou est la capitale du Népal. Le Népal est pays d'asie du sud sur les montagnes les plus hautes du monde de la chaîne montagneuse l'Himalaya, dont l'Everest.

L'altitude de la ville Katmondou est de 1 355 m .

Le Népal est bordé au nord par la Chine (Tibet), au sud; à l'est et à l'ouest par l'Inde.

L'Himalaya est un ensemble de chaînes de montagnes s'étirant sur plus de 2 400 km de long et 250 à 400 km, de large.

Le mont Everest est une montagne située dans la chaîne de l'Himalaya, à la frontière entre le Népal et la Chine.

L'altitude du Mont Everest est de 8 848 m .

2. Calcul de la distance à vol d'oiseau:
Katmondou-Everest

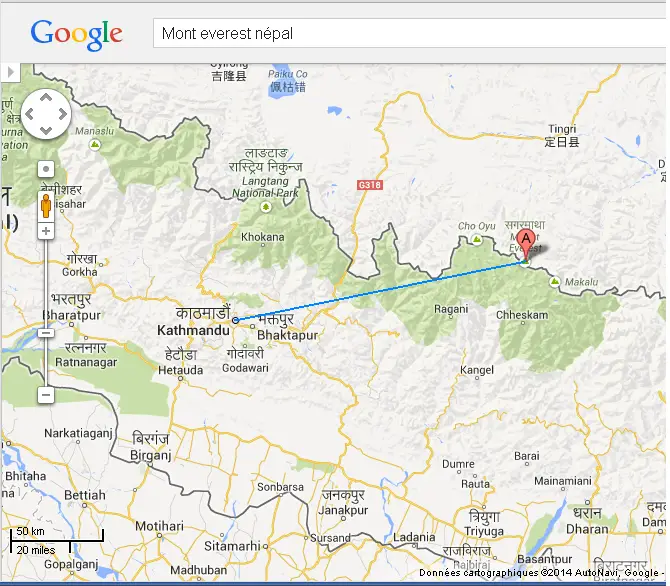
Sur cette carte Google Maps, on lit l'echelle:
3.4 cm correspond à 50 km.

Ensuite, on mesure la distance , qui est la distance à vol d'oiseau de Katmandou au mont Everest, on obtient 10.7 cm.

Un produit croisé donne donc la valeur qui correspondnte (50/3.4) x 10.7 = 157 km.

La distance à vol d'oiseau entre Katmandou et le mont Everest est d'environ 160 km.

3. Estimation du trajet du téléphérique :
Katmondou-Everest
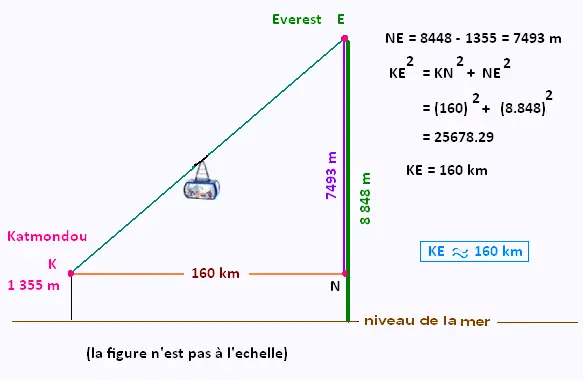