Mathématiques
2
Théorème de Pythagore
Je pratique la Géo
© The scientific sentence. 2010
| Mathématiques 2: Géométrie
Théorème de Pythagore
Autres applications
Une constatation ou une mesure sur un dessin
non codé ne justifient
pas la validité d'un
énoncé en géométrie.
Le but d'une démonstration en Mathématiques
est de prouver la validité
ou la non validité
d'un énoncé, c'est à dire démontrer soit il
est vrai, soit il est faux.
Exercice 1
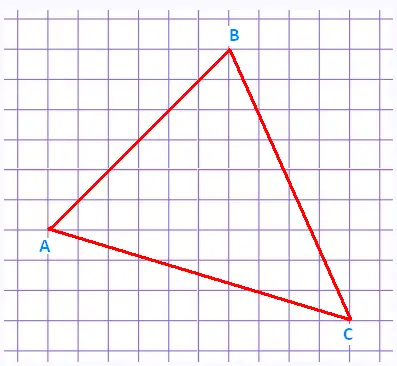
Le triangle ABC est représenté sur un plan cartésien.
Chaque carreau mesure 1 unité x 1 unité.
a) Ce triangle est-il rectangle? Justifier.
b) Calculer l'aire de ce triangle.
Exercice 2
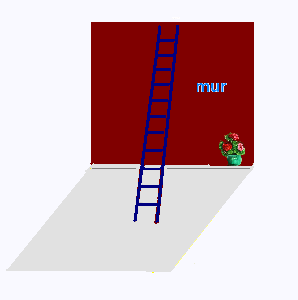
On suppose que le mur est perpendiculaire au sol.
a) Quelle est la hauteur du mur si l'echelle mesure
8.5 m et se trouve à une distance de 2 mètres
du pied du mur ?
b) On rapproche le bas de l'échelle à 1.5 m du pied du
mur.
Quelle est alors la longeur restante de l'échelle
qui dépasse le haur du mur ?
Exercice 3
On veut estimer la longeur d'un téléphérique de l'aéroport
Trudeau à Dormal au Mont-Royal à Montréal.
Sur cette carte (à réaliser sur Google Maps),
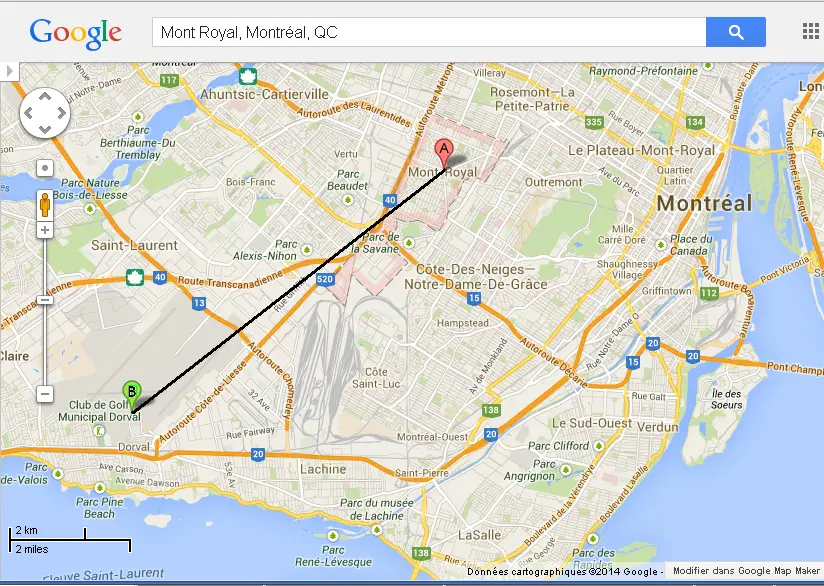
a) lire l'echelle.
b) mesurer la distance, entre A et B qui est la distance
à vol d'oiseau, sur papier (sur écran d'ordinateur), de Trudeau
au Mont-Royal.
c) En déduire la distance à vol d'oiseau, sur
le terrain (valeur réelle), correspondante.
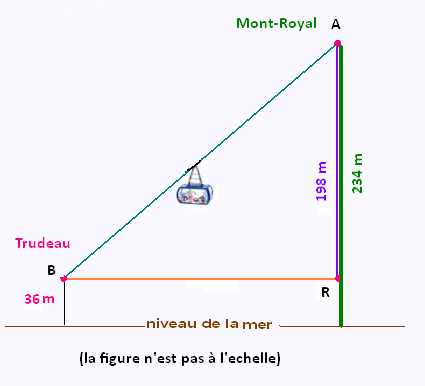
d) Calculer la différence d'altitude entre les
points A et B.
e) Par le théorème de Pythagore, estimer le trajet d'un
téléphérique Trudeau - Mont-Royal.
On donne:
• L'aéroport Trudeau (Dorval) est situé à 36 mètres d'altitude.
• L'altitude de Mont-Royal (Montréal) est de 234 m.
Exercice 4
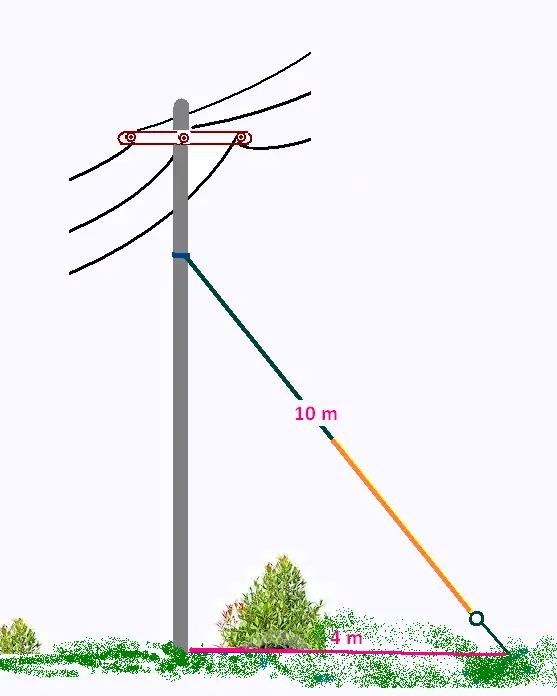
Pour soutenir un poteau de ligne électrique, on l'attache,
à la terre, à 4 m de son pied au moyen d'un cable qui mesure 10 m .
Le cable est attaché au deux-tiers du poteau à partir
du sol.
Quelle est la hauteur du poteau électrique ?
Exercice 5
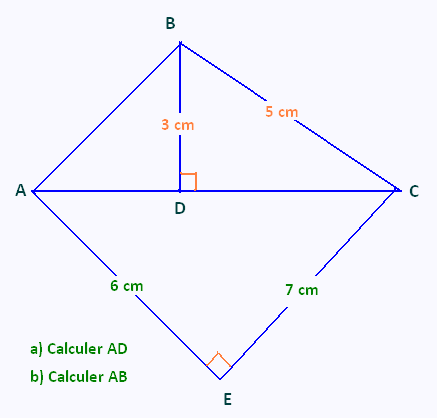
Exercice 6
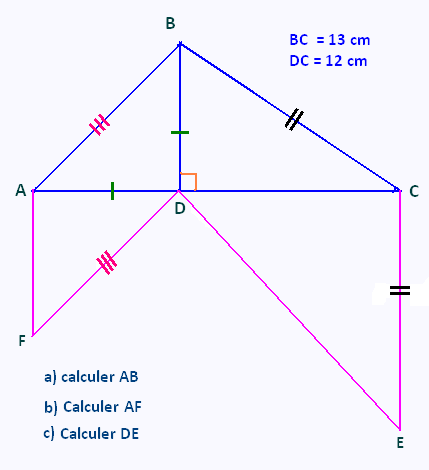
Exercice 7
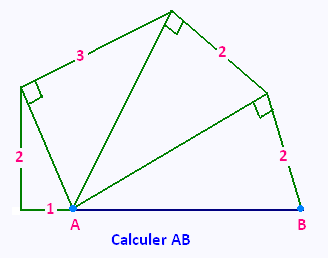
Exercice 8
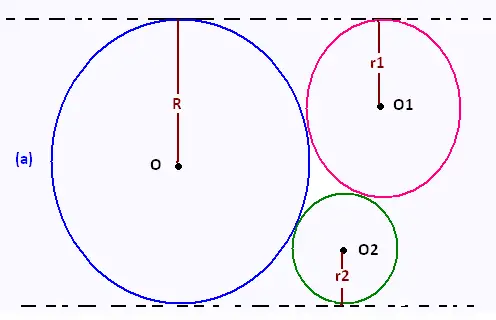
Trois cercles de centre O, O1 et O2 sont tangents extérieurement l'un à l'autre. Les deux droites tangentes
aux cercles sont parallèles.
Calculer le rayon du grand cercle R.
On donne r1 = 4 cm et r2 = 9 cm.
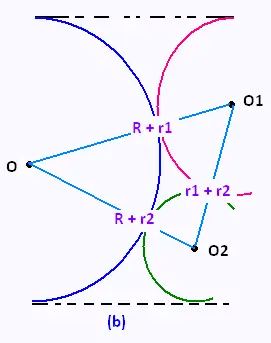
Puisque les cercles sont tangents extérieuremenet,
nous aurons donc::
OO1 = R + r1
OO2 = R + r2
O1O2 = r1 + r2
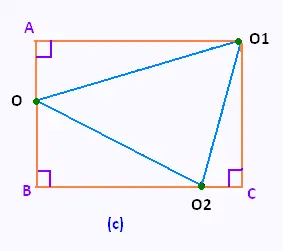
On forme un rectangle AO2BC, et l'on a:
OA = R - r1
OB = R - r2
The théorème de Pythagore s'ecrit:
a) Dans le triangle rectangle OAO1:
OA2 + AO12 = OO12
OA2 + AO12 = OO12
d'où
AO12 = OO12 - OA2
AO12 = (R + r1)2 - (R - r1)2 =
(R + r1 + R - r1)(R + r1 - R + r1) =
2R x 2r1 = 4 Rr1
AO12 = 4 Rr1
(1)
b) Dans le triangle rectangle OBO2:
OB2 + BO22 = OO22
D'où
BO22 = OO22 - OB2 =
(R + r2)2 - (R - r2)2 =
(R + r2 + R - r2)(R + r2 - R + r2) =
2R x 2 r2 = 4 R r2
BO22 = 4 Rr2
(2)
c) Dans le triangle rectangle CO1O2 :
CO12 + CO22 = O1O22
D'où
CO22 = O1O22 - CO12
Or
CO1 = OA + OB = R - r1 + R - r2 = 2R - r1 - r2
CO22 = (r1 + r2)2 - (2R - r1 - r2)2
= (r1 + r2 + 2R - r1 - r2)(r1 + r2 - 2R + r1 + r2) =
2R(2r1 + 2r2 - 2R) = 4 R (r1 + r2 - R)
CO22 = 4 R (r1 + r2 - R)
(3)
Le quadrilatère ABCO1 est un rectangle.
Nous avons donc BC = AO1:
Dans ce rectangle BC = BO2 + CO2. D'où
BO2 + CO2 = AO1.
D'après la formule (1), on a donc
BO2 + CO2 = 2 √(Rr1)
BO2 + CO2 = 2 √(Rr1)
(4)
Nous allons donc combiner les formules
(2), (3) et (4). On a:
2 √(Rr2) + 2 √[R (r1 + r2 - R)] = 2 √(Rr1)
2√(Rr2) + 2√[R(r1 + r2 - R)] = 2√(Rr1)
En simplifiant par 2√R, on obtient:
√r2 + √(r1 + r2 - R) = √r1
ou
√(r1 + r2 - R) = √r1 - √r2
En élevant au carrée, on a:
r1 + r2 - R = r1 + r2 - 2 √(r1r2)

- R = - 2 √(r1r2)
R = 2 √(r1r2)
R = 2√(r1r2)
|
|