Mathématiques: GÉOMETRIE
Exercice 1
ABC est un triangle rectangle en A tel que
AB = 60 m et AC = 80 m .
Le poinr K est le milieu du côté [BC].
Calculer la longueur AK.
Exercice 2
ABCD est un losange. On donne BD = 8 cm et AC = 5 cm.
1) Faire une figure en vraie grandeur
2) Calculer le côté du losange .
Exercice 3
Soit une droite (d) et un point M situé en dehors de la droite (d).
Construire la parallèle à la droite (d) passant par le point G.
Dans chacun des cas suivants, faire une figure, en laissant les traits de constructions.
1) Construction à la règle et à l’équerre.
2) Construction au compas.
 ↓Réponse↑ ↓Réponse↑
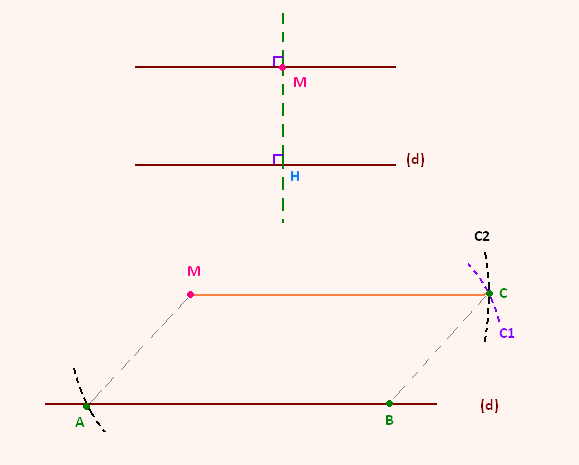
1)
On utilise la propriété suivante:
Si deux droites sont perpendiculaires à une même troisième,
alors elles sont parallèles entre elles.
Avec l'équerre et la règle :
1) À partir du point M, on dresse la perpendiculaire à la droite (d),
qui coupe (d) en H. On obtiont la droite
(MH).
2) On dresse la perpendiculaire à la droite (MH) au point M.
Cette perpendiculaire est la parallèle à la droite (d).
2)
On utilise la propriété suivante:
Un parallélogramme est un quadrilatère dans lequel
les côtés opposés sont de même longueur deux à deux.
Avec le compas:
1) À partir du point M, on trace un arc de cercle qui coupe
la droite (d) au point A.
2) D'un point quelconque B sur la droite (d), on
trace un arc de cercle C1 de rayon égal à MA.
3) Du point M, on trace un arc de cercle C2 de rayon AB
qui coupe C1 en C.
La droite (MC) est la droite parallèle à (d).
Exercice 4
Pour chacun des quadrilatères suivants, faire un schéma à main levé (propre et complet) et donner leurs définitions.
1) un carré ABCD;
2) un losange ABCD;
3) un parallélogramme ABCD ;
4) un rectangle ABCD.
Exercice 5
Pour chacun des quadrilatères suivants, faire un schéma à main levé (propre et complet) et donner les propriétés
de ses diagonales :
1) un carré ABCD;
2) un losange ABCD;
3) un parallélogramme ABCD ;
4) un rectangle ABCD.
Exercice 6
Soit un cercle (C1) de diamètre [AB] avec AB = 8 cm.
M est un point de ce cercle tel que AM = 5 cm.
Tracer le cercle (C2) de centre A passant par M.
1) Faire une figure.
2) Quelle est la nature du triangle ABM ? Justifier.
3) Que représente la droite (BM) pour le cercle (C2) ? Justifier
Exercice 7
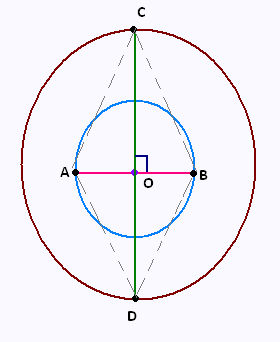
Sur la figure, [AB] est un diamètre du cercle (C1) de centre O,
et [CD] est un diamètre du cercle (C2) de même centre O.
1) Que peut-on dire de O pour les segments [AB] et
[CD] ?
2) Démontrer que ACBD est un losange.
3) Que peut-on en déduire pour les angles ∠BCA et
∠ADB ? Justifer.
Exercice 8
ABC est un triangle tel que
AB = 9 cm, AC = 12 cm et BC = 15 cm.
M est le milieu de [BC].
1) Faire une figure que l’on complétera par la suite.
2) Montrer que ABC est un triangle rectangle.
3) En déduire la longueur MA.
4) Calculer la mesure de l’angle ∠ ACB .
5) Tracer le cercle de diamètre [AB]. Il
recoupe [BC] en D et [MA] en E.
6) Montrer que les droites (AD) et (BE) sont deux hauteurs du triangle AMB. On coloriera le triangle ABM.
7) Que peut-on en déduire pour le point S, intersection des segments [BE] et [AD] ?
8) Placer le point F symétrique du point E par rapport à M.
9) Quelle est la nature du quadrilatère BECF ? Justifier votre réponse.
Exercice 9
1) Donner la définition du centre du cercle inscrit dans un triangle.
2) Donner la définition du centre du cercle circonscrit à un triangle.
Exercice 10
Soit (C) un cercle de centre O et de rayon 6.0 cm.
[AB] est un diamètre du cercle (C). La médiatrice du
segment [BO] coupe le cercle (C) en deux points E et F.
I est le milieu du segment [BO].
1) Démontrer que le triangle BEO est équilatéral.
En déduire la longueur EB.
2) Quelle est la nature du triangle AEB ?
3) Calculer la longueur EA.
4) La parallèle à la droite (AE) passant par I coupe la droite (EB) en J.
Quelle est la nature du triangle IJB ?
5) Calculer JB et IJ
 ↓Réponse↑ ↓Réponse↑
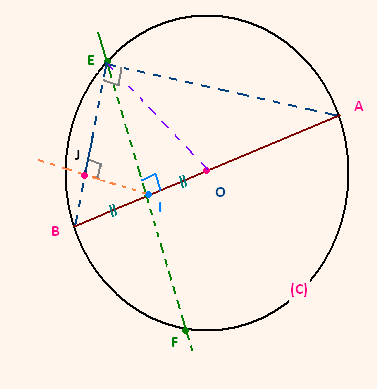
1)
On sait que (EF) est la médiatrice du segment [BO] au point I.
D'après la propriété:
La médiatrice d'un segment est la perpendiculaire à
ce segment et qui passe par son milieu,
on en déduit:
(EF) est perpendiculaire à [BO] et que IO = IB.
La médiatrice (EF) devient la médiane du côté [BO] du
triangle OBE de sommet principal E.
D'après la propriété:
Dans un triangle isocèle, la droite issue du sommet
principal est à la fois hauteur et médiane, on en déduit:
le triangle OBE est isocèle. Donc EB = EO
OB = EO puisque les côtés [OB] et [EO] sont des rayons
du même cercle (C).
Donc OB = EO = EB. Donc le triangle EBO est équilatéral.
EB = valeur du rayon du cercle = 6.0 cm.
EB = 6.0 cm.
2)
Le triangle AEB a pour l'un de ses côtés le diamètre du cercle.
D'après la propriété:
Si un triangle est inscrit dans un cercle de diamètre
l'un de ses côtés, alors ce triangle est rectangle.
Donc AEB un triangle rectangle en E
3)
D'après la propriété de Pythagore:
AB2 = BE2 + AE2
D'où:
AE2 = AB2 - BE2 =
122 - 62 = 3 x 62 = 3 x 36 = 108
AE = 10.40 cm.
4) La parallèle à la droite (AE) passant par I coupe la droite (EB) en J.
L'angle E est droit.
(IJ) est parallèle à (EA)
Donc les angles correspondants E et J sont isométriques.
Ainsi J est un angle droit. Il s'en suit que
le triangle IJB est un triangle rectangle.
5)
(EA) // (IJ):
D'après la propriété de Thalès:
a)
BJ/BE = BI/BA
BJ/6 = 3/12. D'où BJ = 1.5 cm
BJ = 1.5 cm
b)
IJ/AE = BJ/BE
IJ/10.40 = 1.5/6. D'où IJ = 10.40 x 1.5/6 = 2.6 cm
IJ = 2.6 cm
Exercice 11
L'aire d'un terrain est de 400 m2
On en fait une maquette. Pour cela, on réalise une réduction de coefficient 0.05.
1) Par quel coefficient ont été multipliées les longueurs ?
2) Par quel coefficient ont été multipliées les aires ?
3) En déduire l'aire de la maquette en m2 puis en cm2.
Exercice 12
ABCD est un rectangle de centre O tel que AB = 8 cm et AD = 6 cm.
M est un point sur [AB] et N un point sur [CD] tel que AM = CN = 3 cm.
1) Faire une figure.
2) Quelle est la nature du quadrilatère AMCN ? Justifier.
3) Pourquoi le point O est-il le milieu du segment [MN] ?
Exercice 13
1) Construire un parallélogramme ABCD tel que
AB = 5 cm ; AD = 3 cm et l'angle DAB mesure = 120o.
2) Placer le point I milieu de [AB], et le point J milieu de [CD]. Tracer le quadrilatère JBID.
3) Montrer que (IB) et (JD) sont parallèles.
4) Démontrer que IB = DJ.
5) En déduire la nature du quadrilatère JBID. Justifier.
6) Que peut-on en déduire pour les droites (ID) et (BJ) ?
Et pour les segments [ID] et [BJ] ?
NB. Utiliser la propriété:
Si un quadrilatère (non croisé) a une paire de côtés opposés parallèles et de même longueur alors ce quadrilatère est un parallélogramme.
Exercice 14
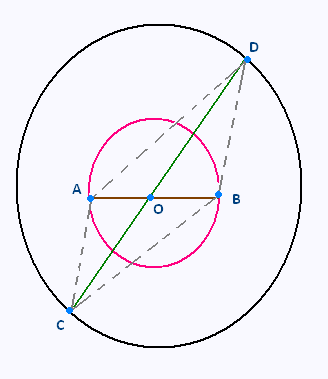
Sur la figure, [AB] est un diamètre du cercle (C1) de centre O,
et [CD] est un diamètre du cercle (C2) de même centre O.
1) Que peut-on dire de O pour les segments [AB] et
[CD] ?
2) Démontrer que ACBD est un parallélogramme.
3) Que peut-on en déduire pour les angles ∠BCA et
∠ADB ? Justifer.
Exercice 15
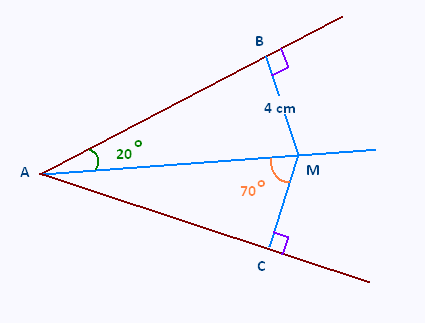
1) Calculer la mesure de l’angle ∠ CAM.
2) Que peut-on en conclure pour le point M ?
Justifier.
3) En déduire la longueur MC. Justifier
Exercice 16
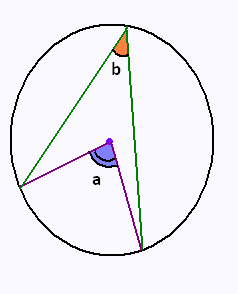
L'angle au centre a et l'angle inscrit b interceptent
le même arc.
Démontrer que a = 2b.
 ↓Réponse↑ ↓Réponse↑
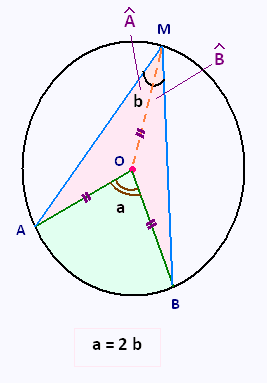
OA = OB = OM = rayon d'un même cercle de centre O.
Donc les triangles OAM et OBM sont isocèles. Ainsi
leurs angles à la base ont même mesure.
D'après les deux propriétés:
• La somme des angles intérieurs d'un triangle est
égale à 180o,
• Un angle plein mesure 360o,
On ecrit:
180 - 2A + 180 - 2B + a = 360.
D'où a = 2(A + B) .
C'est à dire a = 2b
a = 2b
|