Mathématiques
2
Théorème de Pythagore
Je pratique la Géo
© The scientific sentence. 2010
| Mathématiques 2: Géométrie
Théorème de Pythagore
Point mobile sur l'hypoténuse
Distance à l'hypoténuse
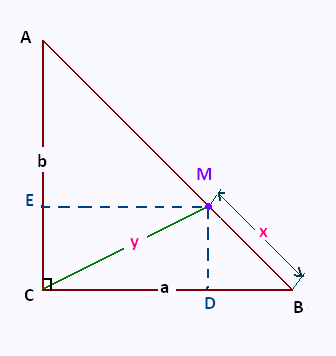
Soit un triangle rectangle en C.
Le point M se déplace sur l'hypoténuse.
Quelle est la position du point M sur l'hypotenuse
pour que sa distance CM du sommet C soit minimale?
D'après la propriété de Pythagore,
AB2 = a2 + b2
Traçons les perpendiculaires ME et MD.
D'après la propriété de Thalès:
x/AB = MD/AC, d'où:
MD = b x/AB
De même:
(AB - x)/AB = ME/BC. d'où:
ME = BC (AB - x)/AB = a (AB - x)/AB =
a (1 - x/AB) =
D'après la propriété de Pythagore,
y2 = MD2 + ME2
Posons z = x/AB, il vient:
y2 = (bz)2 + (a(1 - z))2 =
b2 z2 + a2 (1 - z)2 =
b2 z2 + a2 (1 - 2z + z2) =
b2 z2 + a2 - 2a2 z + a2z2 =
z2 (a2 + b2) - 2a2 z + a2
y2 = z2 (a2 + b2) - 2a2 z + a2
z = x/AB
dy/dz = 0 si 2 (a2 + b2) z - 2a2 = 0 .
D'où:
(a2 + b2) z = a2
z = a2/(a2 + b2) = a2/AB2
x = AB a2/AB2 = a2/AB = a2/√(a2 + b2)
x = a2/√(a2 + b2) = a2/AB
y2 = AB2 a4/AB4 - 2a2 a2/AB2 + a2 =
a4/AB2 - 2 a4/AB2 + a2 =
- a4/AB2 + a2 =
[- a4 + a2(a2 + b2)]/AB2 =
[- a4 + a4 + a2 b2]/AB2 =
[a2 b2]/AB2
y2 = [a2 b2]/AB2
y = ab/AB = ab/√(a2 + b2) = (b/a) x
Application:
a = 5 cm et b = 9 cm. D'où :
x = 25/√(25 + 81) = 25/√106 = 2.43
y = 5 x 9/√106 = 4.37 cm
|
|