Mathématiques: GÉOMETRIE
En Géométrie, on prouve un résultat en passant par trois étapes:
• Je rassemble les données,
• Je démontre en utilsant les propriétés ou les théorèmes
que j'ai appris,
• Je conclus par une phrase.
Exercice 1
Les mesures suivantes correspondent aux longueurs des côtés d’un triangle. Ces triangles
sont-ils rectangle ? Justifier la réponse et donner le sommet de l’angle droit.
| Cas | AB | BC | AC |
| 1 | 8.0 | 12.0 | 4.0 |
| 2 | √40 | 5 | √15 |
| 3 | 2.8 | 9.6 | 10.0 |
| 4 | 17.5 | 14.0 | 10.5 |
| 5 | 1.0 | 5/3 | 4/3 |
Exercice 2
a) Enoncer le théorème de Pythagore.
b) Enoncer la réciproque du théorème de Pythagore.
c) Enoncer la contraposée du théorème de Pythagore.
Exercice 3
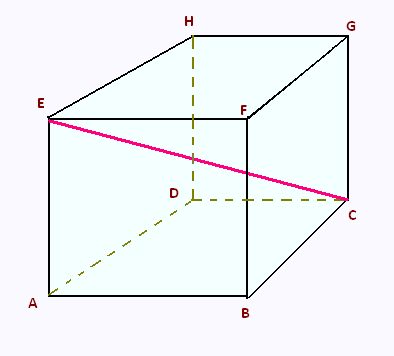
On considère un cube d'arête 8 cm.
Calculer la longueur EC.
Donner le résultat exact puis approché au dixième près.
Exercice 4
Soit un triangle ABC. Compléter le tableau ci-dessous:
| ABC est rectangle
en A | ABC est rectangle
en B |
| AB2 | BC2 | AC2 |
AB2 | BC2 | AC2 |
| 17 | 20 | |
17 | 20 | |
| 5 | | 12 |
5 | | 12 |
| | 25 | 12 |
| 25 | 34 |
| 27 | 43 | |
27 | | 43 |
Exercice 5
Dans un triangle ABC, on construit la hauteur [AH].
On donne:
BC = 14.9 cm
HC = 4.9 cm
AH = 7 cm
Le triangle ABC est–il rectangle en A . Justifier
Exercice 6
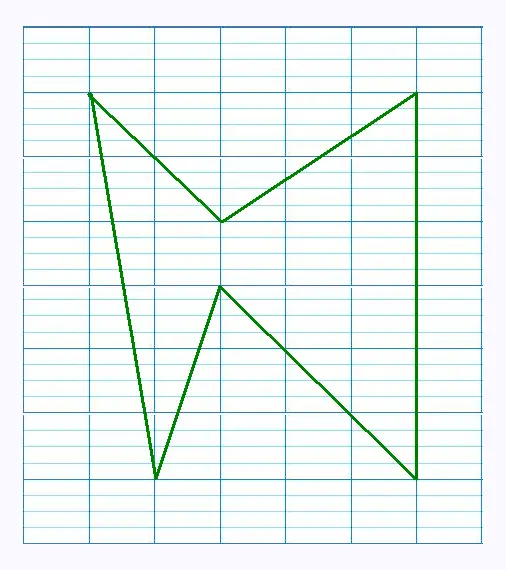
Le côté d’un carreau est 1cm, déterminer le périmètre de la figure:
Exercice 7
Construire un triangle ABC avec les mesures suivantes :
AB = 33 mm ; BC = 40 mm ; AC = 50 mm
a) Montrer que ce triangle est rectangle.
b) Donner son angle droit.
c) Donner le nom du côté AC, du côté BC et du côté AB.
Exercice 8
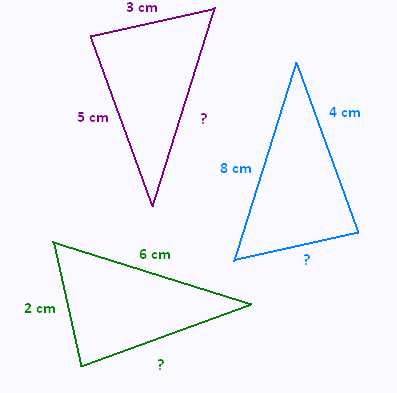
Calculer les longueurs manquantes dans les triangles rectangles ci-dessous. Donner une
valeur au centième près.
Exercice 9
Un triangle ABC est rectangle en A. Son aire est de 64 cm2.
Un des côtés de l’angle droit mesure 8 cm
Déterminer la longueur de l’hypoténuse.
Exercice 10
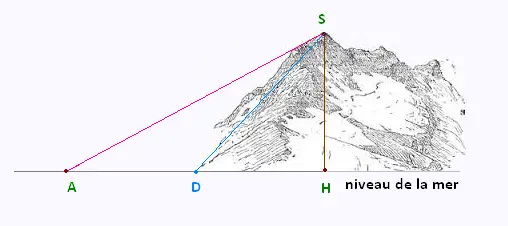
La longeur du cable AS est de 20.55 km.
La hauteur de la montagne est 8.80 km.
Le point D est le milieu du segment [AH].
Calculer la mesure du segment [DS].
Exercice 11
Le périmètre d'un rectangle mesure 100 cm.
Sa largeur mesure 40 cm.
a) Faire un dessin à main levée
b) déterminer la mesure, au dixième près, de la
diagonale de ce rectangle.
Exercice 12
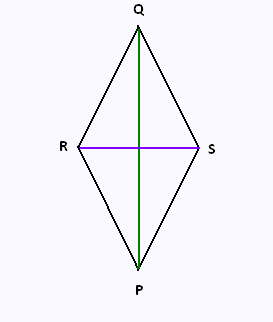
Nommer la figure géométrique ci-contre.
On donne PQ = 15 mm, RS = 10 mm
Calculer le périmètre de cette figure.
Donner le résultat sous la forme exacte, puis
au centième près.
Exercice 13
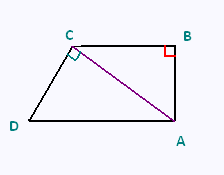
On donne:
AB = 2.00 cm
BC = 3 cm
CD = 2.5 cm
a) Nommer cette figure codée ci-contre.
b) Calculer la longueur du côté [AD].
c) calculer les périmètres des triangles
ABC et ACD.
Exercice 14
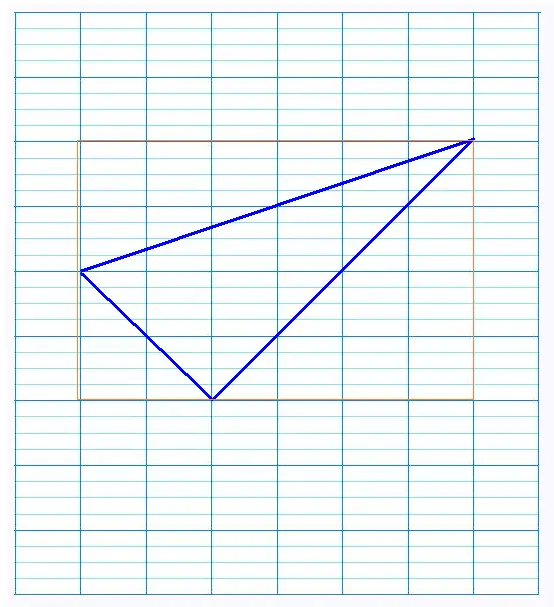
Dans cette figure, 1 carreau = 0.5 cm .
Démontrer que ce triangle est rectangle.
Exercice 15
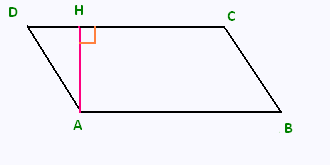
Calculer l’aire du parallélogramme ABCD
sachant que:
HC = 4 dm
CB = 2 dm
AB = 6 dm
Exercice 16
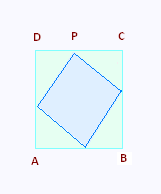
On considère un carré ABCD de 10 cm d'arête, dans lequel on inscrit un autre carré.
Le point P est à 3 cm du point A.
Déterminer l’aire du carré iscrit.
Exercice 17
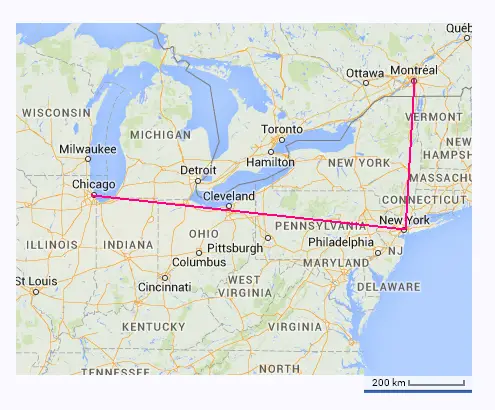
Calculer l'écart entre les trajets Chicago-Montréal et
Chicago-NewYork-Montréal.
On suppose que l'angle formé à NewYork est un
angle droit.
Exercice 18
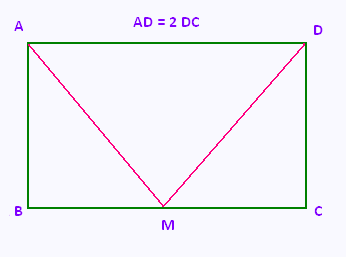
Soit un rectangle ABCD, avec AD = 2 DC = 18 cm,
et M le milieu de [BC].
Démontrer que AMD est un triangle rectangle
en M.
Exercice 19
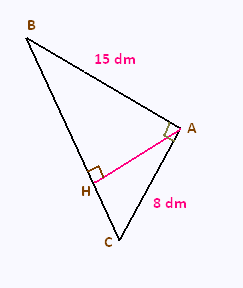
ABC un triangle rectangle en A. H est le pied de la
perpendiculaire issue de A en H.
a) Calculer l’aire du triangle ABC
b) Calculer la mesure de la distance BC.
c) En déduire la mesure de la hauteur [AH].
Exercice 20
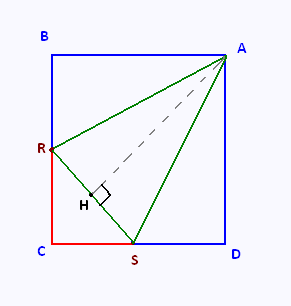
ABCD est un carré de 14 cm de côté.
BR = SD = 5 cm.
a) Calculer RS
b) Calculer AR
c) Calculer AH
d) En déduire l'aire du triabgle ARS
Exercice 21
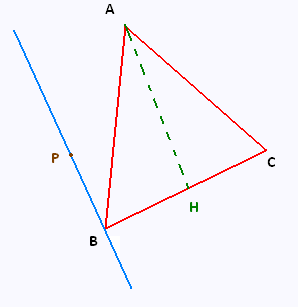
ABC est un triangle équilatéral de côté 12 cm.
a) Calculer la mesure de la hauteur issue du point
A coupant (BC) en H.
Le point P est à 5 cm du point B.
La droite (PB) est parallèle à (AH)
b) Calculer la mesure de la distance [PH].
|
