Mathématiques 2: Géométrie
Théorème de Pythagore
Prisme à base carrée
Exercice 1 : Prisme à base carrée
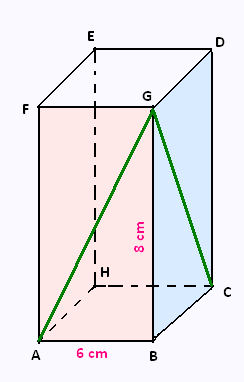 On considère un prisme à base carrée représenté
en perspective cavalière.
On considère un prisme à base carrée représenté
en perspective cavalière.
On trace les diagonales des faces ABGF et BGDC.
a) Calculer la mesure de ces diagonales.
b) Calculer la mesure du côté AC
c) Le triangle AGC est-il un triangle rectangle?
Justifier.
d) Quelle serait la nature du prisme si le triangle AGC
était équilatéral?
Exercice 2: Cube
Vérifier les constructions suivantes et donner
des valeur numériques pour a = 10 cm.
2.1. Triangle équilatéral: perspective cavalière:
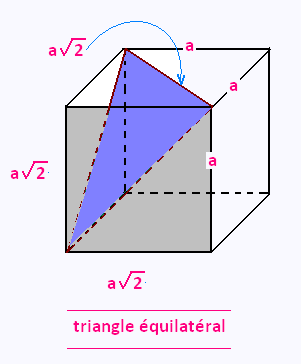
Cube en perspective cavalière:
Triangle diagonal
équilatéral joignant les sommets opposés:
Périmètre = 3 a √2.
Aire = 2 a2.
2.2. Triangle équilatéral: perspective axonométrique:
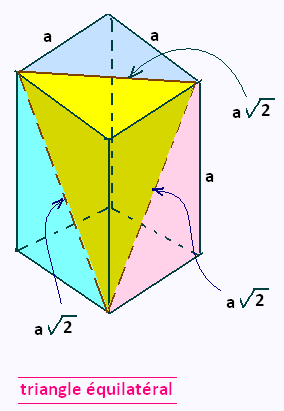
Cube en perspective axonométrique:
Triangle diagonal
équilatéral joignant les sommets opposés:
Périmètre = 3 a √2.
Aire = 2 a2.
2.3. Tige diagonale
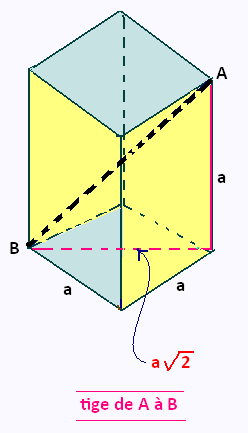
Cube en perspective axonométrique:
Tige diagonale
joignant les deux sommets opposés des deux bases:
Longeur AB = a √3.
2.4. Rectangle diagonal
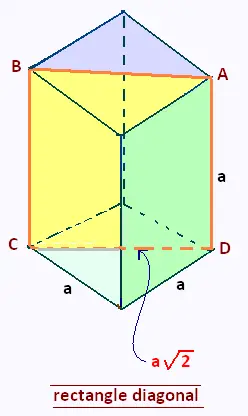
Cube en perspective axonométrique:
Rectangle diagonal
joignant les quatre sommets opposés des deux bases:
Aire = a2√2.
2.5. Triangle rectangle diagonal
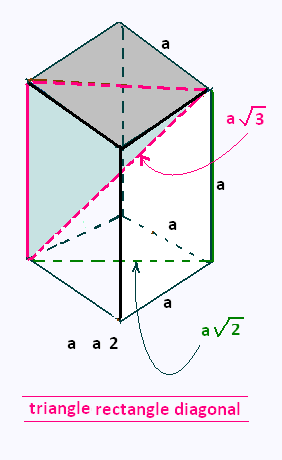
Cube en perspective axonométrique: triangle rectangle diagonal
joignant les trois sommets opposés:
Périmètre = a + a √2 + a √3.
Aire = a2 √2/2.
Exercice 3: Deux cubes
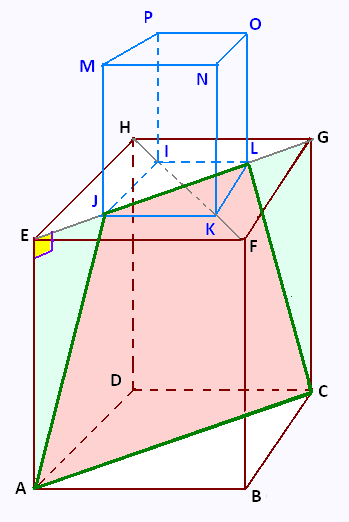
On considère deux cubes:
Le cube ABCDEFGH d'arête 5 cm, et
Le cube IJKLMNOP d'arête 3 cm posé au milieu de la face
supérieure du premier.
1. Calculer le périmètre du trapèze ACJL formé par les diagonales
des bases inférieures des deux cubes.
2. Calculer son aire.
Réponses:
1. Périmètre du trapèze:
a)
AB = BC = 5 cm
Le théorème de Pythagore s'ecrit:
AC2 = AB2 + BC2 =
52 + 52 = 50. D'où:
AC = √50 = 5√2.
b)
JK = KL = 3 cm
Le théorème de Pythagore s'ecrit:
JL2 = JK2 + KL2 =
32 + 32 = 18. D'où:
JL = √18 = 3√2.
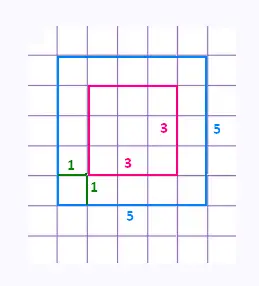
c)
Le petit carré est au milieu du grand carré.
EJ est la diagonale du carré de côté 1. Donc
Le théorème de Pythagore s'ecrit:
EJ2 = 12 + 12 = 2. D'où:
EJ = √2.
d)
Le théorème de Pythagore s'ecrit:
AJ2 = EJ2 + AE2 =
(√2)2 + 52 = 27. D'où:
AJ = 3√3.
De façon similaire,
AJ = CL = 3√3.
e) Le périmètre du trapèze est donc:
P = AJ + JL + LC + CA = 3√3 + 3√2 + 3√3 +
5√2 = 6√3 + 8√2 = 21.71 cm
Périmètre = 21.71 cm.
2. Aire du trapèze:
Aire du trapèze = (JL + AC) x AE /2 =
(3√2 + 5√2) x 5 /2 = 20 √2 = 28.28 cm2.
Aire = 28.28 cm2.
|