Mathématiques 2: Géométrie
Triangle rectangle et cercle
Théorème de Pythagore
Exercice 1
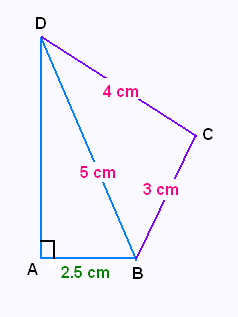
1. Démontrer que BCD est un triangle rectangle.
2. Calculer AD.
3. Démontrer que les points A, B, C et D sont sur un
même cercle et préciser le centre et le rayon de ce cercle.
Exercice 2
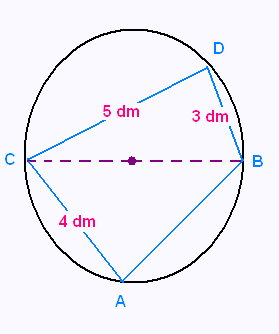
Sur un cercle, on place les points A, B, C, et D.
Les points B et C sont diamétralement opposés.
a) Calculer l'aire du quadrilatère ABCD.
b) Calculer la mesure de l'angle ∠ABC
si celle de l'angle ∠ACB est égale à
30°.
Exercice 3
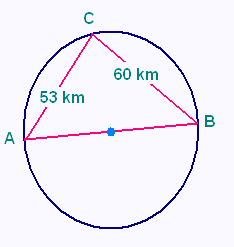
Les points A, B et C représentent des villes.
a) Déterminer la distance entre les villes A et B.
b) Quelle est la nature du triangle ABC ?
c) L'échelle est 1:1000 000.
Construire une figure sur papier selon cette
échelle.
d) Vérifier que l'angle C est droit.
Exercice 4
Tracer un cercle de centre O.
Placer sur ce cercle deux points A et B,
non diamétralement opposés.
Construire la perpendiculaire à (AB) passant
par B, qui coupe le cercle en C.
Montrer que les points A,O et C sont-ils alignés.
Exercice 5
Tracer un cercle de centre O1.
Tracer un cercle de centre O2 tangant
extérieurement au cercle de centre O1.
Construire la tangente (AB) à ces deux
cercles.
Quelle est la nuture du quadrilatère formé par
les points O1, O2, A, et B ?
Exercice 6
Tracer un cercle de rayon 2.5 cm.
Tracer un diamètre [AB] de ce cercle.
C est un point du cercle tel que BC = 3 cm.
Calculer la valeur du côté AC.
Construire un point D tel que
BD = 2 cm et AD = 4.58 cm
Montrer que le point D se trouve sur le cercle.
Exercice 7
Construire un triangle ABC rectangle en A tel que
AB = 3 cm et AC = 4 cm.
a) Déterminer le rayon du cercle circonscrit
au triangle ABC.
b) Construire le cercle circonscrit au triangle ABC .
Exercice 8
a) compléter:
Dans un triangle ..... en un sommet, la hauteur, la bissectrice,
la médiane issue de ce sommet, et la médiatrice de son côté opposé
sont ...... .
Dans un triangle ..... , les hauteurs, médianes,
médiatrices, bissectrices sont ...... .
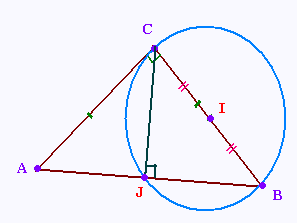
b) Construire un triangle ABC rectangle et isocèle en C tel que
CA = 6 cm.
Placer Le point I milieu du côté [CB] et tracer
un cercle de centre I passant par C. Ce cercle coupe le côté [AB] en J.
c) Montrer que J est le milieu du côté [AB].
d) Calculer la mesure de la hauteur [JC].
Exercice 9
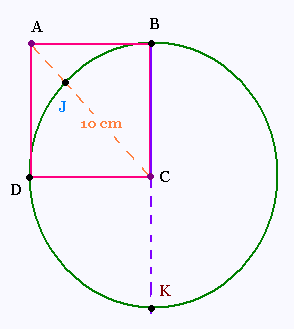
Tracer un carré ABCD dont une diagonale
mesure 10 cm.
Calculer la mesure d'un côté du carré.
. Donner la valeur exacte.
Tracer un cercle de centre C et de rayon [BC] .
Calculer le périmètre de ce cercle.
. Donner la valeur approchée au centième près.
Ce cercle coupe la diagonale [AC] en J.
Calculer la mesure de [AJ].
. Donner la valeur approchée au dixième près.
La droite (BC) coupe le cercle au point K.
Soit un point M tel que: BM 10 cm et KM = 11 cm.
Le poin M appartient-il au cercle? Justifier.
Exercice 10
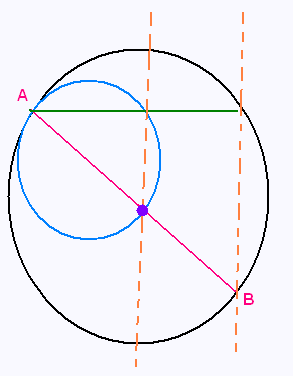
a) Tracer un segment [AB] et nommer O son milieu.
b) Construire le cercle (C1) de diamètre [AB] et
le cercle (C2) de diamètre [AO].
c) Placer un point C sur le cercle (C1) et tracer le segment
[AC], qui doit couper le cercle (C2) en P.
d) Montrer que (OP) est parallèle à (BC).
e) En déduire que P est le milieu de [AC] .
|