Mathématiques
2
Théorème de Pythagore
Je pratique la Géo
© The scientific sentence. 2010
| Mathématiques 2: Géométrie
Théorème de Pythagore
L'hexagone
1. L'apothème d'un hexagone
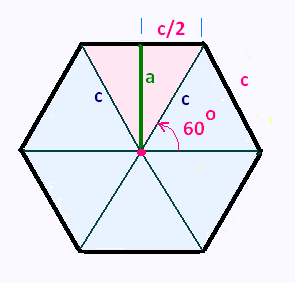
Soit un hexagone de côté c et d'apothème a. Il
a six faces toutes isométriques.
En joignant le centre de l'hexagone
aux deux sommets, on obtient six triangles
isocèles d'angle au sommet 360/6 = 60o.
Les angles à la base d'un triangle isocèle sont égaux.
Chacun mesure (360o - la mesure de l'angle au sommet)/2 =
(360o - 60o)/2 = 60o.
Les trois angles de ce triangle sont donc isométriques et
chacun mesure 60o.
Ainsi le triangle est équilatéral. Donc ses trois
côtés sont isométriques.
Par définition, l'apothème est la hauteur d'un point
au milieu du côté d'un polygone.
Le théorème de Pythagore s'ecrit:
(c/2)2 + a2 = c2. D'où:
a2 = c2 - (c/2)2
= 3c2/4
a2 = 3c2/4
Donc
a = (c/2)√3
2. Triangle dans un prisme à base hexagonale

Un prisme régulier à base héxagonale a pour côté
c et pour apothème a.
Une base du prisme est parallèle à sa hauteur.
Le théorème de Pythagore s'ecrit:
BC2 + AB2 = AC2
D'où:
BC2 = AC2 - AB2
= h2 - (2a)2
BC2 = h2 - (2a)2
or
(2a)2 = (2 x (c/2)√3)2 =
(c √3)2 = 3 c2. Donc
BC2 = h2 - 3 c2
BC = √[h2 - (2a)2]
• Périmètre = BC + AC + AB = √[h2 - (2a)2] + h + 2a
• Aire = (2a) x h/2 = a h .
2. Autre triangle dans un prisme à base hexagonale

Le côté de l'hexagone est égal à 8 cm.
La hauteur du prisme est égale à 12 cm.
a) Calculer l'apothème de la base.
b) Calculer le périmètre du triangle ABC.
c) Calculer l'aire du triangle ABC.
|
|