Mathématiques 45: Géométrie:
Relations métriques dans un triangle rectangle
Nous allons trouver quatre relations métriques
dans un triangle rectangle, just en ecrivant les
rapports de similitude de deux triangles semblables.
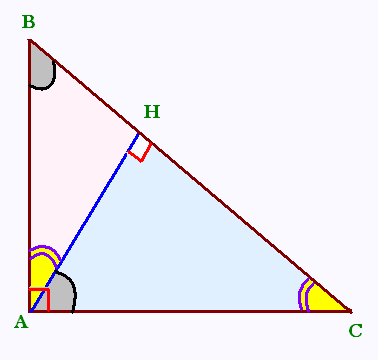
Dans le triangle ABC rectangle rectangle en A, on utlise :
. Le petit triangle rectangle ABH et le grand triangle rectangle ABC, et
. Le petit triangle rectangle ABH et le moyen triangle rectangle ACH,
. Le moyen triangle rectangle ACH et le grand triangle rectangle ABC,
pour démontrer les trois premières relations;
puis l'aire du triangle ABC pour trouver la dernière relation.
Relation 1 :
Les angles ∠HAB et ∠C sont congrues, ainsi les
triangles HAB et ABC sont semblables (cas AA).
Les rapports de similitude sont:
AB/BC = BH/AB
D'où AB2 = BC . BH
AB2 = BC . BH
Relation 2 :
Les triangles ACH et ABH sont semblables (cas AA).
Les rapports de similitude sont:
AB/AC = AH/HC = BH/AH
D'où AH2 = BH . CH
AH2 = BH . CH
Relation 3 :
Les angles ∠CAH et ∠B sont congrues, ainsi les
triangles ACH et ABC sont semblables (cas AA).
Les rapports de similitude sont:
AC/BC = CH/AC
D'où AC2 = BC . CH
AC2 = BC . CH
Relation 4 :
L'aire du triangle rectangle ABC =
AB x AC/2 = AH x BC/2.
D'où AB x AC = AH x BC
AB x AC = AH x BC
Exemple:
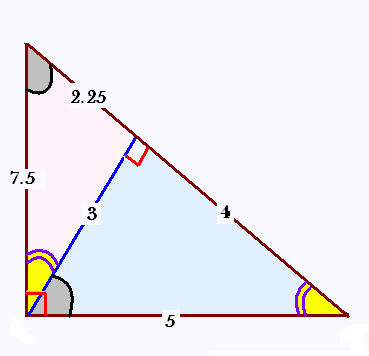
On peut vérifier que les mesures (en unités) dans ce triangle
vérifient les quatres relations métriques.
|