Mathématiques 2: Géométrie
Triangle rectangle
Théorème de Pythagore

Exercice 1 : Completer

Le théorème de Pythagore est un théorème en géométrie ... . Il relie dans une formule les longueurs des côtés dans un triangle .... .

Le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.

ou

Le carré de l’.... est égal à la...
des carrés des deux côtés de l'angle ... .

ou encore

Le carré de l’.... est égal à la
somme des carrés des ... .

Si dans un triangle, le.... de la longueur du plus grand côté est égal à la .....des carrés des longueurs des deux autres côtés, alors ce triangle est ..... et le plus grand côté de ce triangle est son .... qui est opposée à l’.... droit.

ou

Si dans un .... quelconque, le carré d'un côté est égal à la somme des .... des deux autres , alors ce triangle est ... .

Exercice 2

a) Trouver les triplets pythagoriciens parmi les triplets suivants:

• (1,2,3)
• (3,4,5)
• 6,8,10)
• (4, 7, 9)
• (5,12,13)
• (12,16,20)
• (7,24,25)
• (11,60,61)
• (16,63,65)
• (30,40,50)
• (24,45,51)
• (11, 25,15)
• (20,48,52)
• (28,96,100)
• (60,80,100)
• (9,40,41)
• (10,20,30)
• (28,45,53)
• (11,60,61)
• (16,63,65)
• (33,56,65)

b) Quels sont ceux qui sont primitifs ?

Exercice 3

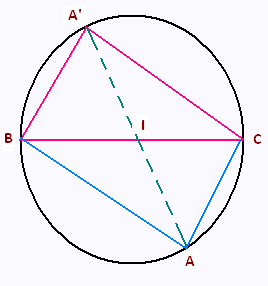Tracer un triangle ABC rectangle en A.

a) Qu'appele-t-on le côté BC ?

Soit I le milieu de l'hypoténuse.

b) Comment sont les segments [IB] et [IC]?

Construire le symétrique A' du point A par rappoort à I.

c) Quelle est la nature du quadrilatère ABA'C ?

d) Montrer que c'est aussi un rectangle.

e) En deduire que IA = IB = IC

Tracer le cercle passant par les points A, B et C.

f) Qu'appele-t-on le côté BC ?

g) Que peut-on dire du cercle de centre I et de rayon [IA] ?

h) Calculer la mesure de la grande cathète dans le triangle BAC sachant que la petite cathète est égale au rayon du cercle de mesure 5 cm.

Exercice 4

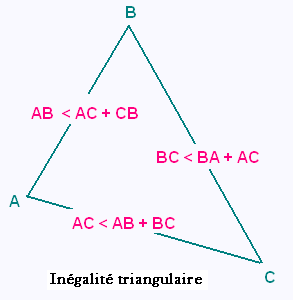On considère le triangle ABC de dimensions:

AB = 5 cm, BC = 7 cm et AC = 14 cm.

a) Montrer que le triangle ABC n'est pas rectangle.

b) Montrer que ce triangle ne peut pas exister.

Exercice 5

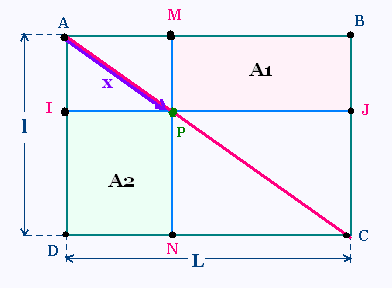
On considère un rectangle de longueur L et de largeur l.

Sur une diagonale on déplace un point P d'une distance x à partir du smmet A.

On obtient donc deux rectangles d'aires A1 et A2.

a) Montrer que les deux aires A1 et A2 sont égales.

b) Ou faut-il placer le point P pour que l'aire commune (A1 = A2) soit maximale?

Exercice 6

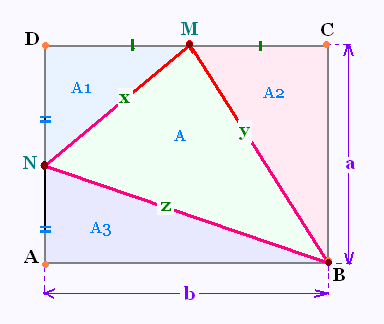
Soit un rectangle ABCD de largeur a et de longueur b.

Le point M est le milieu du côté CD. Le point N est le milieu du côté AD.

a) calculer l'aire du rectangle ABCD.

b) Calculer les aires A1, A2 et A3 des trois triangles NDM, MCB et ABN respectivement.

c) En déduire l'aire du triangle MNB

d) On pose:

BN = z
NM = x
MB = y

Calculer le carré du côté z, x et y

e) Utiliser le théorème de Pythagore pour montrer que le triangle NBM n'est pas rectangle.

f) Donner le pourcentage des aires A1, A3 et A par rapport à l'aire du rectangle ABCD.

g) Quelle doit être la relation entre les côtés a et b pour que le triangle NMB soit rectangle.

Exercice 7

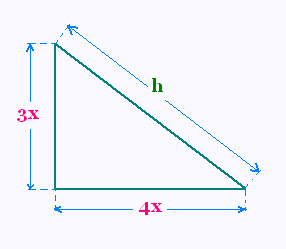
On considère un triangle rectangle de dimensions variables.

a) Trouver les valeurs des cathètes lorsque l'hypoténuse h est égale à 10 m.

b) Trouver la valeure de x lorsque l'aire du triangle vaut 108 m².

c) Trouver la valeure de x en dm lorsque l'hypoténuse du triangle rectangle est égale à 2 - 5 x.