Mathématiques 2: Algèbre:
   Exercices de révision:
      Inégalités

1. Compléter par le symbole <, > ou = qui convient :

1. 1.6 ... 824
2. 332 ... – 211
3. – 34 ... – 23
4. 0.33 ... 1/3
5. 3/7 ... 12/21
6. 44/8 ...43/8
7. - 4/22 ... 4/43
8. - 8/8...- 23/4
9. 2/3 ... 3/2
10. - 1/2 ... 3.5
11. 1/2 ... - 33/2
12. - 3.5 ... - 2.5

2. Ecrire l'inégalité dont x est le premier membre

1. – 2 < x
2. 3 + x > 6
3. – 4 > x + 3
4. 22 + x < 0
5. – 12 > x
6. – 34 < x - 4
7. – 5 - x < 0
8. - 7 - x < - 3
9. – 14 < x - 1
10. – 4 - x < - 32
11. - 10 - x < - 1

3. Résoudre les inéquations suivantes

1. 2x ≥ 10
   
2. 60x < 240
   
3. - 6x > 12
   
4. 14 ≤ - 7x
   
5. 4 < 7x
   
6. - 3x > 12
   
7. - 9 ≤ - 3x
   
8. 21x ≤ 14
   
9. - 12 ≥ - 6x
   
10. 1.4x ≥ - 3.2
    
11. 0.3 < 0.25x
    
12. 5x - 1 ≥ 4
    
13. - 18x + 9 ≤ - 9
    
14. 3x - 5 < x + 7
    
15. - 2x + 11 < 5x + 31
    
16. - 4x + 9 ≥ 8x - 3
    
17. - 2x + 1 ≥ - 2x + 2
    
18. - 4x + 15 ≤ 5x
    
19. - 3x - 4 > 5x
    
20. - x < 1 + x
    
21. 7x + 15 > - 6
    
22. - 4x + 9 < 8x - 3
    
23. - 2x + 1 ≤ - 2x + 2
    
24. - 4x + 15 ≥ 5x
    
25. - 3x - 4 < 5x
    
26. - x > 1 + x

4. L’inégalité x ≥ 7 est-elle vraie pour :

1. x = 7
2. x = - 2
3. x = – 12
4. x = + 3.5
5. x = 5
6. x < 2
7. x < - 4
8. x > 12
9. x ≥ 10

5. On considère le nombre N = 235.567

1)    Déterminer la troncature du nombre N :

a)    à l’unité
b)    au dixième
c)    au centième
d)    au millième


2)    Déterminer l’arrondi du nombre N:

a)    à l’unité
b)    au dixième
c)    au centième
d)    à la dizaine
e)    à la centaine

6. Écrire un encadrement du nombre N = 235.567

a)    à l’unité
b)    au dixième
c)    au centième
d)    au millième

7. Troncature et arrondi

1)    Déterminer la troncature du nombre √5:

a)    au dixième
b)    au centième
c)    au millième

2) Déterminer l’arrondi du nombre √5:

a)    au dixième
b)    au centième
c)    au millième


8. Troncature et arrondi

1) 234.48 est la troncature au centième d’un nombre x.

a) Est-il possible que x soit égal à 234.50 ?, à 234.488 ?, ou à 234.480 ?

b) Écrire un encadrement de x d'amplitude 0,01.


2) - 14.7 est l’arrondi au dixième d’un nombre y.

a) Est-il possible que y soit égal à 14.72 ? , à - 14.72 ?, ou à - 14.77 ?

b) Écrire un encadrement de y d’amplitude 0,1.


9. Comparer les expressions algébriques suivantes:

a)    x² + 2 et x + 1
b)    2(x + 3) et 7 + 2x
c)    x² – 3x + 1 et – 3x + 4


10. Résoudre les inéquations suivantes:

a)    2x + 2 > 12
b)    - 4x + 8 < 32
c)    x + 2 > 22
d)    -5x - 3 ≥ 38
e)    - x + 2 < 12
f)    - 4x + 8 ≤ 32
g)    7x + 6 > 45
h)    -4x + 8 ≥ 30
i)    6x + 2 > 12
j)    - 44x + 80 < 124


11. Encadrement d'une variable x:

1. Déterminer un encadrement du nombre x, sachant
que : – 11 ≤ – 2x – 5 ≤ 3

2. Représenter sur une droite graduée les valeurs possibles du nombre x.


12.solutions sur une droite graduée:

Résoudre les inéquations suivantes et représenter, si c'est possible, les solutions sur une droite graduée:

1.   2x – 5 ≤ 3(x – 1)
2.   10 – 4x + 3(2x – 1) < 7x – 5
3.   – 12x – 2 – (5 – 6x) ≥ - 5x +1
4.   (- 2x + 1)/2 > (5x + 2)/3
5.   (2x + 1)/2 > (5x + 2)/5
6.   (2x + 1)/2 < (5x + 2)/5


13. systèmes d'inéquations du 1er degré à une inconnue:

Résoudre les systèmes suivants et représenter les solutions sur une droite graduée:


1. $\large\color{brown}{ \begin{cases} 3(x - 1) - 3(2 - 3x) <= 10x + 1 \\ 12 - 4(3 - 2x) < 5 - 2(1 + 2x) - 10 (2 - x) \end{cases} }$

2. $\color{brown}{ \begin{cases} 2x - 2(x - 1) \lt \frac{x + 2}{3} \\ 4(x + 1) \le 2 - 2(1 - x) \end{cases} }$

Problème 1

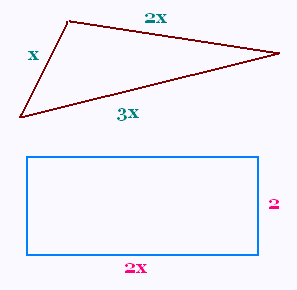
On veut construire un triangle de côtés x, 2x, et 3x et un rectangle de longueur 2x et de largeur 2; mais il y a des des spécifications à respecter.

La contrainte est que le périmètre du triangle doit être inférieur ou égal au périmètre du rectangle.

a) Traduire cette contrainte par une inéquation.

b) Résoudre cette inéquation.

c) La valeur x = 0 est bien une solution de cette inéquation, mais est-elle convenable au problème posé ?

d) Quelle est l'ensemble des solutions réalisabless ?

Problème 2

La somme de trois entiers consécutifs est comprise entre 6 et 15.

1. Quelles sont les valeurs possibles du plus petit de ces trois nombres ?

2. Quelles sont les valeurs possibles du plus grand de ces trois nombres ?

Problème 3

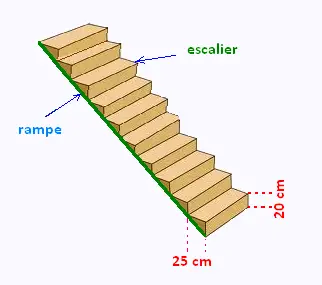
Sur une rampe, on construit un escalier de 25 cm de marche et 20 cm de contremarche.

1. Utiliser le théorème de Pythagore pour montrer que la rampe est plus courte que l'escalier.

2. Pourquoi construit-on alors des escaliers?

Problème 4

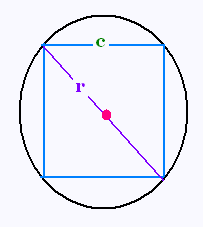
1. Utiliser la formule de Pythagore pour montrer que la mesure du côté du carré c est égale à r√2.

2. Montrer que l'aire du carré est plus petite que celle du cercle circonscrit à ce carré.