Mathématiques 2: Algèbre
Pourcentages
Exercice 1
Dans une classe de 26 élèves, 12 parlent Anglais 10 parlent Français, et le reste parle Espagnol.
Traduire ces situations en pourcentages.
Exercice 2
 Dans un litre de jus d'orange, il y a 650 mL d'eau.
Dans un litre de jus d'orange, il y a 650 mL d'eau.
Quel est le pourcentage de jus d'orange ?
Exercice 3

Un magasin vend des motos. Il accorde des rabais de 12% sur les prix marqués.
1. Le prix marqué est de 3200 $. Quel est le prix à payer
selon les soldes du vendeur?
2. Au prix à payer, il faut ajouter une taxe de 15%.
Quel est le prix final à payer?
Exercice 3
Dans une urne, il y a 38 billes vertes, 22 rouges, et
20 jaunes.
Quels sont les pourcentages de chaque couleur?
Exercice 4
Le prix d'un livre de Mathématiques est de 125 $ taxes
comprises.
a) Quel est le prix du livre sans taxes ?
b) Quel est le pourcentage des taxes sur le prix
du livre ?
Exercice 5
15 oranges de 200 g chacune produisent au total 1 litre
de pure jus d'orange .
Quel est le pourcentage de jus
contenu dans les 15 oranges ?
1 litre de jus d'orange pèse environ 1.05 kg.
Exercice 6

Joe vend sa Plymouth Grand Voyager à 3500 $.
Il l'avait acheté, 10 années auparavant, à 35 000 $.
a) De combien cette voiture a perdu de sa valeur ?
b) A quel pourcentage cette perte correspond-elle ?
c) A quel pourcentage la perte annuelle correspond-elle ?
Exercice 7
a) Un nombre exprimé en % est égal à 37%.
Quel est ce nombre?
b) Les 15% d'un nombre valent 4.5.
Quel est ce nombre?
Exercice 8
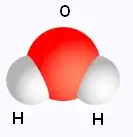
L'eau contient deux fois plus d'hydrogène que
d'oxygène. Ainsi le symbole de l'eau est
H2O.
a) Quel est le pourcentage d'oxygène dans l'eau.
b) Quel est le pourcentage d'hydrogène dans l'eau.
Exercice 9

Une banque accorde des intérets de 10% l'année.
on y place un montant de 185 $.
a) Que devient ce montant dans une année ?
b) Que devient ce montant dans 5 ans ?
c) Que devient ce montant dans 10 ans ?
Exercice 10

Voici les proportions d'ingrédients que Jacynthe a
utilisés pour faire une pâte à baguette française:
• 220 g de farine T55,
• 180 g d’eau à 30 °C,
• 12 g de sel,
• 4 g de levure de boulanger.
a) Quel est le pourcentage de chaque ingrédient?
Mais la pâte est trop molle.
Elle doit rajouter de la farine jusqu'à ce que
la masse totale de farine occupe 62% de la masse
de la pâte tout en gardant les mêmes proportions
entre les trois autres ingrédients.
b) Quel est alors le nouveau pourcentage des
ses trois ingrédients ?
Indications:
Patte molle:
Masse totale = 220 + 180 + 12 + 4 = 416 g.
• farine : 220/416 = 53%
• eau : 180/416 = 43%
• sel: 12/416 = ...%
• levure: 4/416 = 1%
Patte adéquate:
Le pourcentage qui reste pour les trois
ingrédients est égal à 100 - 62 = 38
• farine : 38 x 62% = ...
• eau : 38 x 43% = 16%
• sel: 38 x 3% = ...
• levure: 38 x 1% = ...
Exercice 11 résolu
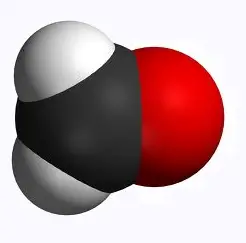
On considère un ensemble de molécules de 3 sortes,
dont :
• 20% contiennent du carbone (C),
• 40% contiennent de l'oxygène (O), et
• 60% contiennent de l'hydrogène (H).
Il y a 56 molécules qui contiennent à la fois les trois types
d'atomes.
Tandis que toutes les autres molécules contiennent exactement
deux types d'atomes.
Combient a-t-on de molécules ?
Soit m le nombre cherché total de molécules.
Soit x le nombre total de molécules qui contiennet H et C , mais pas O,
Soit y le nombre total de molécules qui contiennet H et O , mais pas C,
Soit z le nombre total de molécules qui contiennet C et O , mais pas H,
L'intersection des trois ensembles, s = 56 molécules,
contient à la fois H, C, et O.
Aucune molécule ne contient un seul atomes.
Un diagrame de Venn permet d'eclaircir le problème:
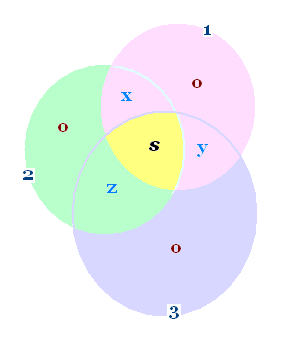
Nous avons
m = x + y + z + s
(0)
Nous avons aussi
• 20% m = x + y + 56 (1)
• 40% m = x + z + 56 (2)
• 60% m = y + z + 56 (3).
En additionnant les trois équations (1), (2), et (3) membre à membre, on
obtient:
1.2 m = 2(x + y + z + 56) + 56
En utilisant la première équation (0), on a:
1.2 m = 2(m) + 56
2m - 1.2 m = 56
0.8 m = 56
m = 56/0.8 = 70
Nous avons 70 molécules.
|