Mathématiques 2: Géométrie :
Exercices de révision:
Quadrilatères
1. Completer
|
Un parallélogramme est un .....
dont les côtés .... sont deux à deux parallèles.
|  |
|
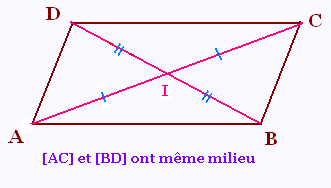
Dans un parallélogramme les ...... se
coupent en leur milieu.
Si ABCD est un parallélogramme alors [AC] et [BD] ont même ....
|
Un quadrilatère non croisé dont les diagonales se coupent
en leur milieu est un ......
Si [AC] et [BD] se coupent en leur milieu et ABCD est un
quadrilatère non croisé alors ABCD est un ....... .
|
|
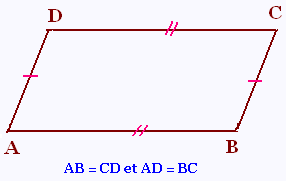
Dans un parallélogramme, les côtés opposés ont
même .......
ABCD parallélogramme alors AB = CD et AD = BC
|
Un quadrilatère non croisé dont les côtés opposés ont
même ....... est un parallélogramme.
si AB = CD et AD = BC alors ABCD parallélogramme.
|
|
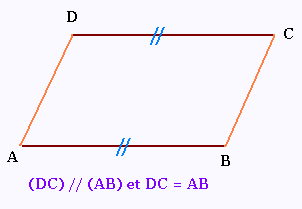
Dans un parallélogramme, deux côtés opposés sont ..... et
ont même longueur.
ABCD parallélogramme alors (AB) // (BC) et AB = CD
|
Un quadrilatère non croisé dont 2 côtés opposés sont ...... et
de même longueur est un parallélogramme.
si (AB)//(CD) et AB = CD alors ABCD est un parallélogramme.
|
|
|
Un parallélogramme possède un centre de ...... qui est
l’intersection des diagonales. Il n'a pas
d'axe de symétrie.
|
|
Un rectangle est un ........ qui possède quatre
angles .......
|  |
|
Un rectangle est un ........ ayant un angle
droit.
Un parallélogramme ayant un angle droit est un
...........
Si ABCD est un .......... et mes(Â) = 90° alors ABCD rectangle
|
|
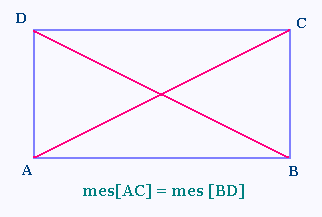
Un rectangle est un parallélogramme dont les diagonales
ont même ..............
Si ABCD est un rectangle alors AC = BD
|
Un ............ dont les diagonales ont même longueur
est .......
Si ABCD est un parallélogramme et AC = BD alors ABCD rectangle
|
|
Un rectangle possède 2 axes de .......... (les médiatrices des côtés)
et 1 ...... de symétrie (intersection des diagonales).
|
|
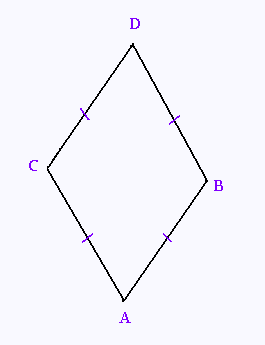
Un losange est un ....... dont les 4 côtés sont de
même ...........
|  |
|
Un losange est un ....... ayant 2 côtés
consécutifs de même longueur.
|
Un ........... ayant 2 côtés consécutifs de même
longueur est un losange.
Si ABCD est un parallélogramme avec AB = BC alors ABCD est un ..........
|
|
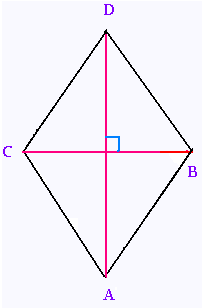
Un losange est un parallélogramme dont les ...........
sont perpendiculaires.
Si ABCD est un losange alors (AC) ⊥ (BD)
|
Un ............. dont les diagonales sont perpendiculaires
est un .............
Si ABCD parallélogramme et (AC) ⊥ (BD) alors ABCD
est un losange.
|
|
Un ......... possède 2 axes de .......... (ses diagonales) et 1
centre de symétrie (l’intersection des diagonales).
|
|
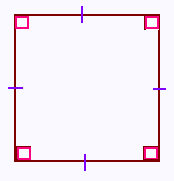
Un carré est un ............ ayant 4 côtés de même longueur
et 4 angles ...............
|  |
|
Un carré est à la fois un rectangle et un .............
Un carré a donc toutes les propriétés du rectangle et du ............
|
Pour montrer qu’un ......... soit un carré, il faut montrer que c’est un ......... et un ...........(en utilisant les réciproques).
|
|
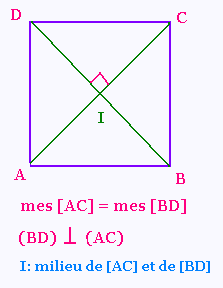
Les diagonales d’un carré se coupent en leur .........., elles
sont perpendiculaires et de même ............
|
Un quadrilatère non croisé ayant des diagonales
qui se coupent en leur ........., perpendiculaires et
de même longueur est un ...........
|
|
Un carré possède 4 axes de ........... (ses 2 diagonales et ses 2 médiatrices des
côtés) et 1 centre de symétrie (l’........... des diagonales).
|
2. Exercices
2.1. Exercice 1
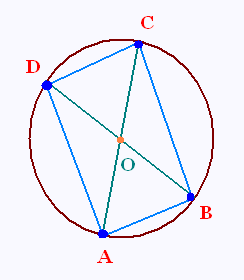 On représente deux diamètres [AC] et [BD]
d'un cercle de centre O.
On représente deux diamètres [AC] et [BD]
d'un cercle de centre O.
On joint les points A, B, C, et D sur
le cercle. On obtient un quadrilatère.
Montrer que ce quadrilatère est un rectangle.
2.2. Exercice 2
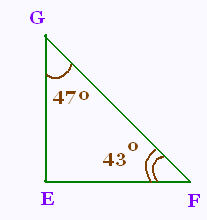 a) Calculer la mesure de l'angle FEG.
a) Calculer la mesure de l'angle FEG.
b) Tracer la parallèle à EF passant par le point G et
la parallèle à EG passant par le point F. Ses parallèles se
coupent au point H. Montrer que le quadrilatère GEFH est
un rectangle.Ses parallèles se
coupent au point H. Montrer que le quadrilatère GEFH est
un rectangle.
2.3. Exercice 3
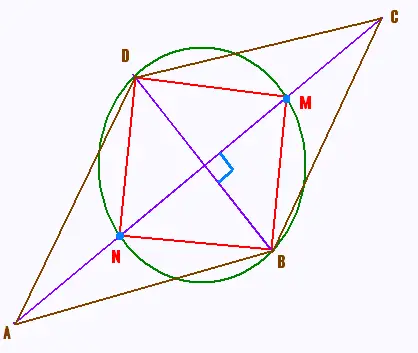 ABCD est un parallélogramme.
ABCD est un parallélogramme.
a) D'après les informations codées sur la figure,
préciser la nature du quadrilatère ABCD.
Justifier en précisant la propriété utilisés.
b) Le cercle de diamètre [BD] coupe la droite (AC) en
M et N.
Quelle est la nature du quadrilatère NBMD?
Justifir en précisant la propriété utilisée.
2.4. Exercice 4
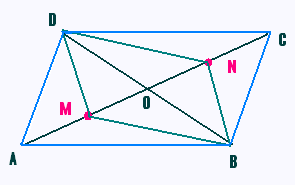 ABCD est un parallélogramme de centre O.
ABCD est un parallélogramme de centre O.
M est le milieu de segment [OA]
N est le milieu de segment [OC]
a) Expliquer pourquoi OM = ON.
b) En déduire que le quadrilatère MDNB
est un parallèlogramme.
2.5. Exercice 5
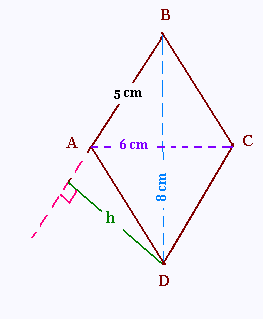 a) construire un losange ABCD tel que:
AC = 6 cm et BD = 8 cm.
a) construire un losange ABCD tel que:
AC = 6 cm et BD = 8 cm.
b) Calculer l'aire du losange ABCD.
c) Calculer la hauteur relative au
côté [AB] sachant que AB = 5 cm.
2.6. Exercice 6
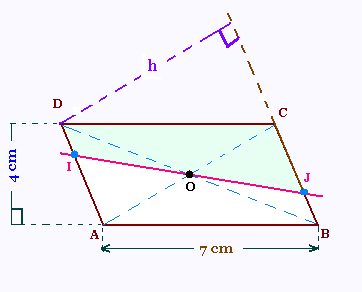 ABCD est un parallélogramme de centre O, de
base 7 cm et de hauteur 4 cm.
ABCD est un parallélogramme de centre O, de
base 7 cm et de hauteur 4 cm.
a) Calculer l'aire du parallélogramme ABCD.
On trace une droite quelconque passant par le centre O,
coupant [AD] en I et [BC] en J.
b) Calculer l'aire du quadrilatère IDCJ.
c) Calculer la hauteur h relative au côté BC
si ce côté mesure 5 cm.
2.7. Exercice 7
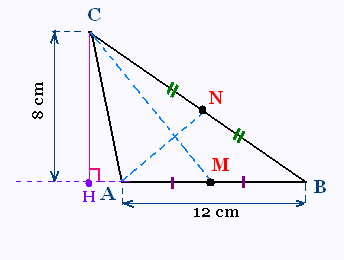 Avec les informations codées sur la figure, calculer
l'aire de chacun des triangles ABC, ACM, et ABN.
Avec les informations codées sur la figure, calculer
l'aire de chacun des triangles ABC, ACM, et ABN.
2.8. Exercice 8
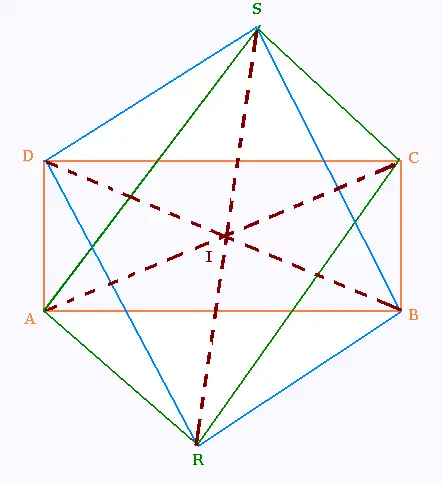
ABCD est un rectangle.
ARCS est un rectangle.
Montrer que le quadrilatère DSBR est
aussi un rectangle.
☛ Solutions
|