Mathématiques 2: Géométrie:
Exercices de révision:
Solides
1. Compléter
Partie 1:
Polyèdre
Un solide est une portion d'espace limitée
par une .... .... .
Un polyèdre est un solide limité par des
faces planes formées par des ....... .
Le ........ d'un polyèdre est la figure
plane obtenue par un mise à plat de sa surface; dont
chacune des faces est relié à au moins une autre
face par une arête commune.
Prisme
Un prisme est une ....... formé par deux
faces isométriques et parallèles appelées bases.
Les parallélogrammes qui relient ces deux bases sont
appelés des .......... ..........
Un prisme est droit si ses faces
latérales sont des ........
Un prisme est régulier s'il est droit
et en plus sa base est un polygone ............
La hauteur d'un prisme droit est la distance entre
les deux ...... du prisme.
Pyramide
Une pyramide est polyèdre formé d'une seule ..........
et dont les faces latérales sont des .......... Ces
triangles ont un même sommet commun appelé apex.
Une pyramide est ......... si la hauteur abaissée
à partir de l'apex se trouve au milieu de la base.
Une pyramide est régulière si elle droite et en
plus sa base est formée d'un polygone ............
La hauteur d'une pyramide droite est la distance entre
l'.......... et la base de la pyramide.
Partie 2:
Cercle:
Un cercle est une ligne ..... où tous
les points sont à égale distance d’un même
point appelé le ...........
Rayon:
Un rayon est le ....... qui relie
un point quelconque du ..... au centre de ce
cercle.
Diamètre:
Un diamètre est le segment qui relie
deux points du cercle et passant par le
.......... .
Le diamètre est le .......... du rayon.
Si d est le diamètre du cercle et r son rayom,
alors
d = ... x r et r = d/....
.
Corde :
Une corde est un segment qui relie deux
points quelconques d’un .......
Le ..... est la plus longue corde du cercle.
Arc de cercle:
Un arc de cercle est une portion de .......
délimitée par deux points qui forment une corde.
Angle au centre:
Un Angle au centre est l'angle
formé par deux ....... Le sommet de l’angle
correspond donc au centre du cercle.
Circonférence:
La circonférence est la longueur du
contour d’un cercle ou le ........ d’un cercle.
On calcule la circonférence à partir du diamètre
du cercle ou à partir de son ........
C = π x ...... ou C = 2π........
Disque
Un disque est une surface plane délimitée
par un ....... Son aire est égale à πr2.
Aire du disque = ......r2
Secteur
Un secteur est une portion de disque délimitée
par deux rayons.
Son aire est égale à:
(Mesure de l'angle au centre du secteur en °)x
(Aire totale du disque)/.........°
Aire totale d'un solide
Le calcul de l’aire totale d’un solide
correspond à l’aire de tous les polygones
ou cercles qui le ......
Le calcul se fait en trois étapes :
On calcule l’aire des .... ou de la base;
On calcule l’aire des .... latérales;
On ....... le tout.
2. completer
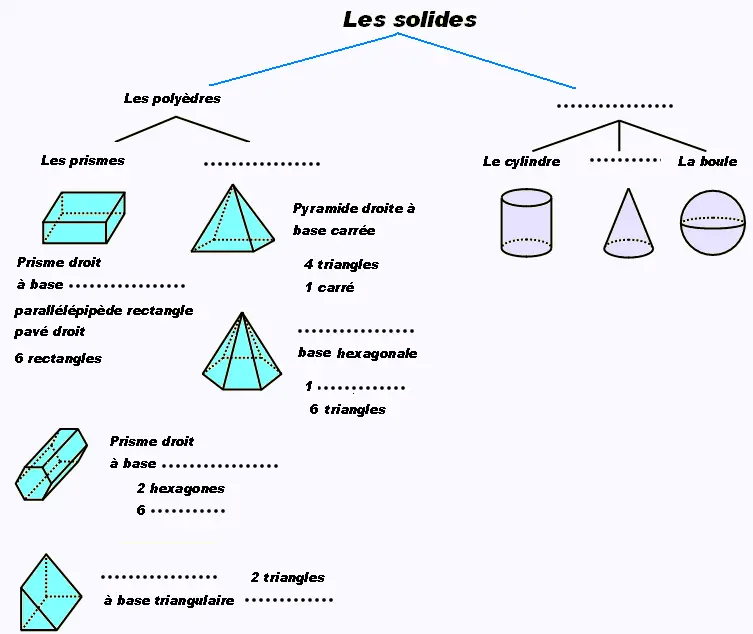
3. Calculer
1. 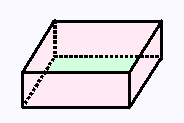
Calculer l'aire totale de ce prisme à
base rectangulaire:
Largeur = 5 cm
Longeur = 4 cm
Épaisseur = 20 mm
2. 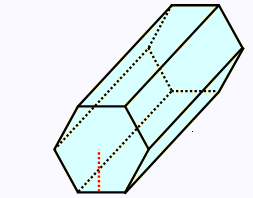
Calculer l'aire totale de ce prisme à
base hexagonale:
côté = 4 cm
Apothème = 6 cm
Hauteur = 8 cm
3. 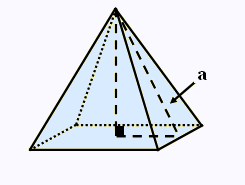
Calculer l'aire totale de cette pyramide à base
carrée :
côté = 8 cm
Hauteur = 100 mm
Utiliser d'abord la relation de Pythagore pour
trouver l'apothème .
4. 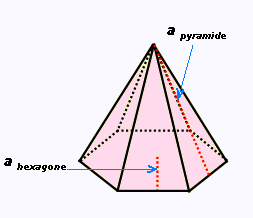
Calculer l'aire totale de cette pyramide à base
hexagonale :
Apothème hexagone = 8 cm
Apothème pyramide = 0.12 m
côté = 60 mm .
5. 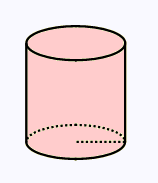
Calculer l'aire totale de ce cylindre de révolution
(droit) :
Rayon = 8 m
Hauteur = 10 m
6. 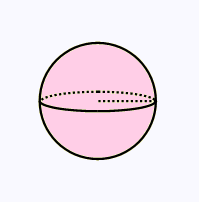
Calculer l'aire totale de cette sphère :
Rayon = 6400 km
Quelle est le pourcentage occupé par une
surface de 10 millions de km2?
7. 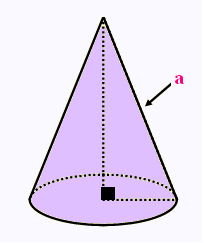
Calculer l'aire totale de cecône :
Rayon = 10 m
Hauteur = 20 m
Utiliser d'abord la relation de Pythagore pour
trouver l'apothème a du cône.
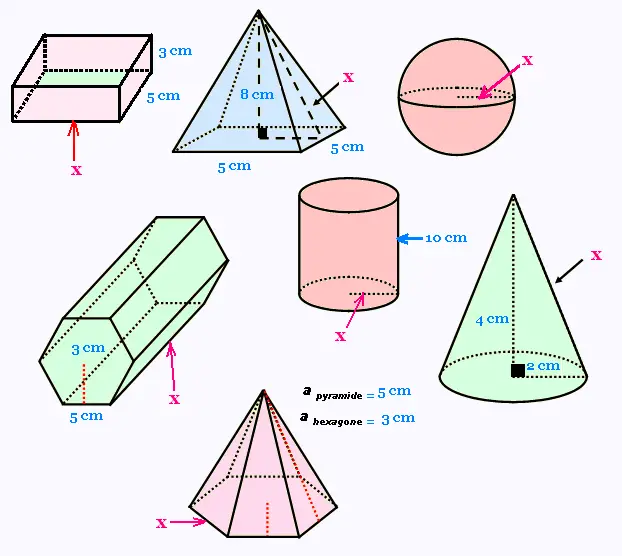
4. Calculer la valeur manquante x
L'aire totale de tous les solides est
la
même et est égale à
2 dm2.
Exercice 1:
Determiner la circonférence d'un cercle si;
a) r = 4 cm
b) D = 3 m
c) Un angle au centre de mesure 60° intercepte
un arc de 4 cm.
Exercice 2:
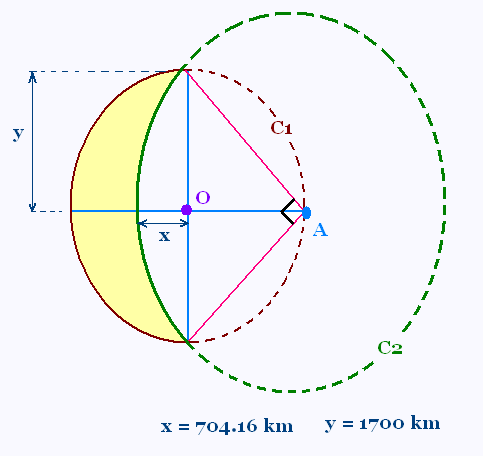
Un croissant de lune est formé de deux arcs
des cercles C1 de centre O et C2 de
centre A.
a) Quel est le périmètre du croissant?
b) Quel est l'aire du croissant?
Exercice 3:
Voici une voiture du type "coccinelle" qui roule et qui fait des roulades:
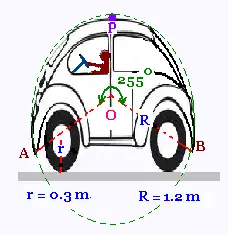
Cette voiture roule sur une certaine distance, ensuite lorsque
le contact au point A touche le sol, la voiture fait une roulade
sur une deuxième distance.
Quel est le nombre minimal de tours que doit effectuer une
roue de l'automobile si la voiture parcourt une distance
de 9 m en effectuant une seule roulade (une seule rotation
du conducteur sur lui même)?
Exercice 4:

Le rayon de ce disque de fruits et légumes est égal
à 3 mètres.
a) Quel est le diamètre du disque?
b) Quelle est la circonférence du disque?
c) Quel est le nombre de secteurs dans le disque?
d) Quel est la mesure de l'angle au centre de chaque secteur?
e) Quel est la mesure des angles des triangles formés par les
secteurs?
f) Quelle est la nature des triangles formés?
g) Quelle est la longueur de l'arc intercepté par
chaque secteur?
h) Quelle est l'aire du disque?
i) Quelle est l'aire de la surface occupée par les
nectarines, si elles représenten 30% du secteur
où elles se trouvent?
j) Quelle est le pourcentage en surface, par rapport au disque
entier, occupée par les nectarines, si elles occupent 30% du secteur
où elles se trouvent?
Exercice 5:
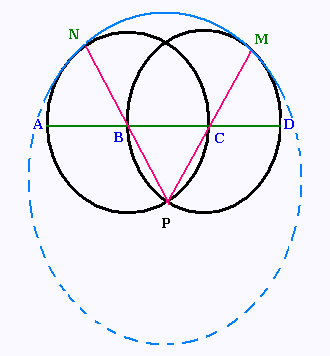
Une arche AD est formée de trois arcs de cercle AN, NM, et MD où
les cercles de centre B et C ont même rayon.
Quelle est la longueur de cette arche?
Pour la partie 2 du 1 et les cinq derniers exercices,
les
réponses se trouvent dans le lien suivant:
☛ Solutions
|