Mathématiques 2: Géométrie
Triangle rectangle
Cercle circonscrit à un triangle
Exercice 1
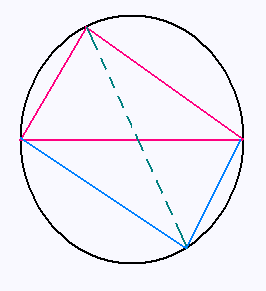
Tracer un triangle ABC rectangle en A.
a) Qu'appele-t-on le côté BC ?
Soit I le milieu de l'hypoténuse.
b) Comment sont les segments [IB] et [IC]?
Construire le symétrique A' du point
A par rappoort à I.
c) Quelle est la nature du quadrilatère ABA'C ?
d) Montrer que c'est aussi un rectangle.
e) En deduire que IA = IB = IC
Tracer le cercle passant par les points A, B et C.
f) Qu'appele-t-on le côté BC ?
g) Que peut-on dire du cercle de centre I et
de rayon [IA] ?
h) Compléter:
1) Théorème :
Si un triangle est .... alors le centre de son cercle circonscrit est le milieu de son ..... et la médiane relative à l’hypoténuse a pour mesure la .... de celle de l’hypoténuse.
2) Sa réciproque:
Si, dans un ..., un triangle a pour sommets les extrémités d’un ..... et un point quelconque de ce cercle alors ce triangle est ..... .
Exercice 2
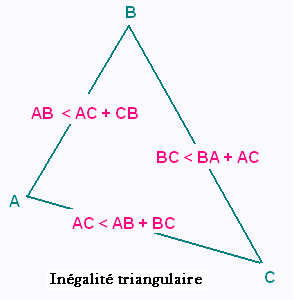On considère le triangle ABC de dimensions:
AB = 5 cm, BC = 7 cm et AC = 14 cm.
a) Montrer que que le triangle ABC n'est pas rectangle.
b) Montrer que ce triangle ne peut pas exister.
Exercice 3
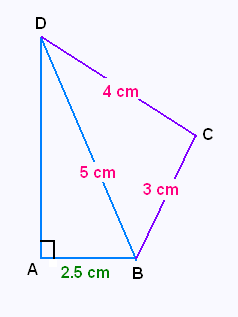
1. Démontrer que BCD est un triangle rectangle.
2. Calculer AD.
3. Démontrer que les points A, B, C et D sont sur un
même cercle et préciser le centre et le rayon de ce cercle.
Exercice 4
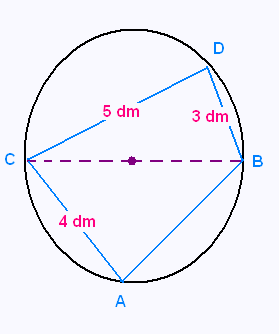
Sur un cercle, on place les points A, B, C, et D.
Les points B et C sont diamétralement opposés.
a) Calculer l'aire du quadrilatère ABCD.
b) Calculer la mesure de l'angle ∠ABC
si celle de l'angle ∠ACB est égale à
30°.
Exercice 5
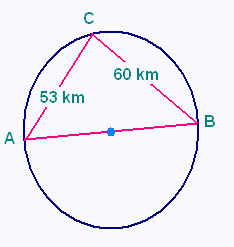
Les points A, B et C représentent des villes.
a) Déterminer la distance entre les villes A et B.
b) Quelle est la nature du triangle ABC ?
c) L'échelle est 1:1000 000.
Construire une figure sur papier selon cette
échelle.
d) Vérifier que l'angle C est droit.
Exercice 6
Tracer un cercle de centre O.
Placer sur ce cercle deux points A et B,
non diamétralement opposés.
Construire la perpendiculaire à (AB) passant
par B, qui coupe le cercle en C.
Montrer que les points A,O et C sont-ils alignés.
Exercice 7
Tracer un cercle de centre O1.
Tracer un cercle de centre O2 tangant
extérieurement au cercle de centre O1.
Construire la tangente (AB) à ces deux
cercles.
Quelle est la nuture du quadrilatère formé par
les points O1, O2, A, et B ?
Exercice 8
Tracer un cercle de rayon 2.5 cm.
Tracer un diamètre [AB] de ce cercle.
C est un point du cercle tel que BC = 3 cm.
Calculer la valeur du côté AC.
Construire un point D tel que
BD = 2 cm et AD = 4.58 cm
Montrer que le point D se trouve sur le cercle.
Exercice 9
Construire un triangle ABC rectangle en A tel que
AB = 3 cm et AC = 4 cm.
a) Déterminer le rayon du cercle circonscrit
au triangle ABC.
b) Construire le cercle circonscrit au triangle ABC .
Exercice 10
a) compléter:
Dans un triangle ..... en un sommet, la hauteur, la bissectrice,
la médiane issue de ce sommet, et la médiatrice de son côté opposé
sont ...... .
Dans un triangle ..... , les hauteurs, médianes,
médiatrices, bissectrices sont ...... .
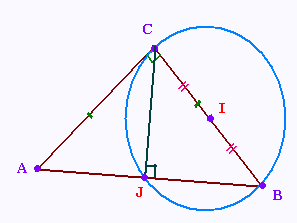
b) Construire un triangle ABC rectangle et isocèle en C tel que
CA = CB = 6 cm.
Placer Le point I milieu du côté [CB] et tracer
un cercle de centre I. Ce cercle coupe le côté [AB] en J.
c) Montrer que J est le milieu du côté [AB].
d) Calculer la mesure de la hauteur [JC].
Exercice 11
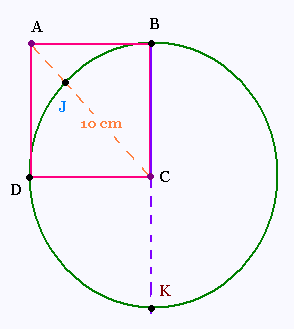
Tracer un carré ABCD dont une diagonale
mesure 10 cm.
Calculer la mesure d'un côté du carré.
. Donner la valeur exacte.
Tracer un cercle de centre C et de rayon [BC] .
Calculer le périmètre de ce cercle.
. Donner la valeur approchée au centième près.
Ce cercle coupe la diagonale [AC] en J.
Calculer la mesure de [AJ].
. Donner la valeur approchée au dixième près.
La droite (BC) coupe le cercle au point K.
Soit un point M tel que: BM 10 cm et KM = 11 cm.
Le poin M appartient-il au cercle? Justifier.
Exercice 12
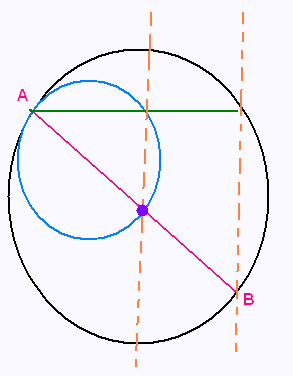
a) Tracer un segment [AB] et nommer O son milieu.
b) Construire le cercle (C1) de diamètre [AB] et
le cercle (C2) de diamètre [AO].
c) Placer un point C sur le cercle (C1) et tracer le segment
[AC], qui doit couper le cercle (C2) en P.
d) Montrer que (OP) est parallèle à (BC).
e) En déduire que P est le milieu de [AC] .
Exercice 13
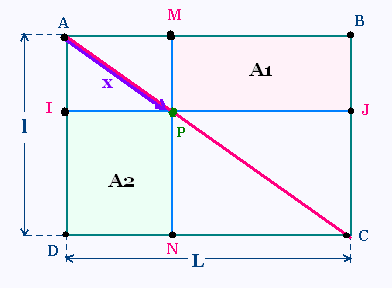
On considère un rectangle de longueur L
et de largeur l.
Sur une diagonale on
déplace un point P d'une distance x
à partir du smmet A.
On obtient donc
deux rectangles d'aires A1 et A2.
a) Montrer que les deux aires A1 et A2 sont
égales.
b) Ou faut-il placer le point P pour que l'aire
commune (A1 = A2) soit maximale?
Exercice 14
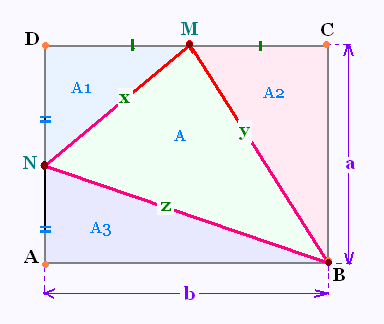
Soit un rectangle ABCD de largeur a et de
longueur b.
Le point M est le milieu du côté CD.
Le point N est le milieu du côté AD.
a) calculer l'aire du rectangle ABCD.
b) Calculer les aires A1, A2 et A3 des trois
triangles NDM, MCB et ABN respectivement.
c) En déduire l'aire du triangle MNB
d) On pose:
BN = z
NM = x
MB = y
Calculer le carré du côté z, x et y
e) Utiliser le théorème de Pythagore pour
montrer que le triangle NBM n'est pas rectangle.
f) Donner le pourcentage des aires A1, A3 et A
par rapport à l'aire du rectangle ABCD.
g) Quelle doit être la relation entre les côtés
a et b pour que le triangle NMB soit rectangle.
Exercice 15
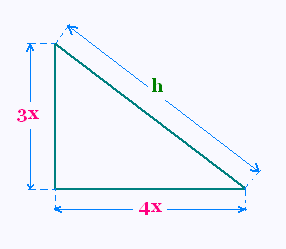
On considère un triangle rectangle de dimensions variables.
a) Trouver les valeurs des cathètes lorsque l'hypoténuse
h est égale à 10 m.
b) Trouver la valeure de x lorsque l'aire du triangle vaut
108 m2.
b) Trouver la valeure de x en dm lorsque l'hypoténuse
du triangle rectangle est égale à 2 - 5 x.
|