Mathématiques 2: Géométrie:
Triangles et parallèles
Théorème des
milieux et théorème de Thalès
Exercice 1
Compléter:
1. Théorème des milieux
La droite qui .... par les milieux de deux côtés d'un triangle est appelée droite des milieux.
Théorème 1 :
Si dans un triangle une droite passe par les ..... de deux côtés, alors cette droite est .... au troisième côté de ce triangle.
Théorème 2 :
Si dans un triangle un segment passe par les milieux de deux côtés, alors sa longueur est égale à la ..... de celle du troisième côté de ce triangle.
Théorème 3 :
Si dans un triangle une droite passe par le milieu d’un côté et est ..... au second, alors cette droite coupe le troisième côté en son .....
2. Droite parallèle dans un triangle
Propriété de Thalès:
Si dans un triangle une droite passe par deux points des côtés et si elle est ...... au
troisième côté, alors elle forme un nouveau triangle dont les longueurs des côtés sont
proportionnelles à celles des côtés du ...... initial.
C'est à dire:
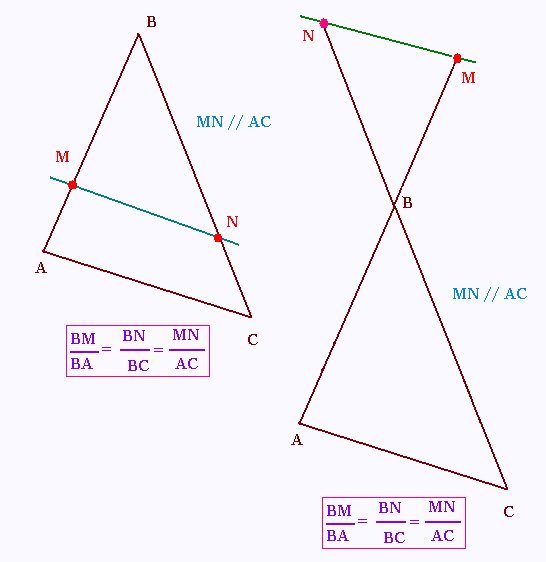
Si dans un triangle ABC, M appartient à [AB], N à [BC] et (MN) est ..... à (AC), alors
AM/AB = AN/AC= MN/BC
On remarque qu'il y a deux configurations
possibles.
Exercice 2
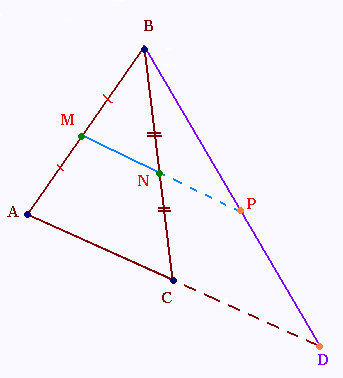
a) Tracer un triangle ABC.
b) Placer les milieux M du côté AB et N
du côté BC
c) Démontrer que (MN) // (AC)
d) Prolonger les droites (MN) et (AC)
e) Tracer la demi droite issue du point B qui
coupe la droite (MN) en P et
la droite (AC) en D.
f) Montrer que P est le milieu de [BD].
Exercice 3
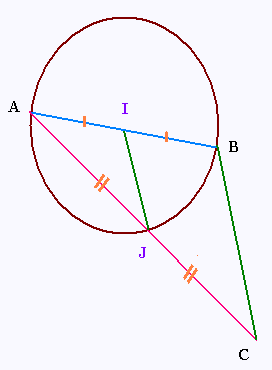
a) Tracer un cercle de centre I, de rayon 4cm.
b) Placer deux points A et B tels que le
segment [AB] soit un diamètre de ce cercle.
c) Placer un point J sur le cercle.
d) Construire le point C symétrique de A par rapport à J.
e) Démontrer que (IJ) // (BC)
f). Calculer la mesure du [BC].
Exercice 4
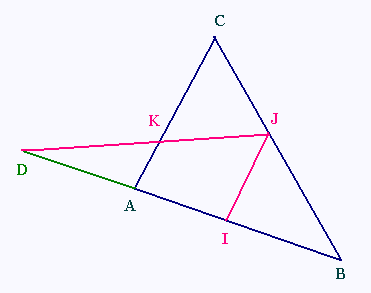
I milieu de [AB]
J milieu de [BC]
A milieu de [DI]
a) Démontrer que K est le milieu de [DJ].
b)Comparer AK et KC
Exercice 5
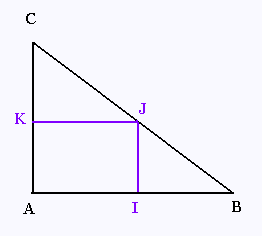
On considère un triangle ABC rectangle en A. I, J et K sont les milieux respectifs des côtés [AB], [BC] et [AC].
a) Montrer que des droites (IJ) et (AB) son perpendiculaires.
b) Montrer que des droites (JK) et (AC) son perpendiculaires.
c) Préciser la nature du quadrilatère AKJI.
Exercice 6
Tracer un triangle scalène ABC. placer les points I, J et K, milieux respectifs des côtés [AB], [BC] et [AC].
Prouver que la droite (BJ) coupe le segment [KI] en son milieu.
Exercice 7
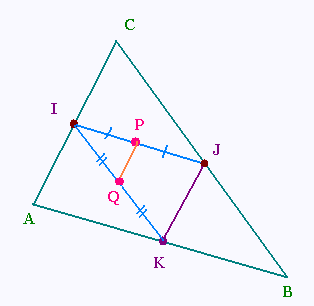
On considère un triangle ABC . I, J et K sont les milieux respectifs des côtés [AC], [BC] et [AB].
On désigne par P et Q les milieux respectifs de [IJ] et [IK].
a) Montrer que des droites (PQ) et (AC) sont parallèles.
b) Préciser la nature du quadrilatère PJKQ.
Exercice 8
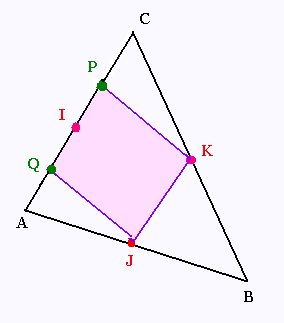
On considère un triangle ABC . I, J et K sont les milieux respectifs des côtés [AC], [AB] et [BC].
On désigne par P et Q les milieux respectifs de [IC] et [IA].
a) Préciser la nature du quadrilatère PQJK.
b) Montrer que le quadrialtère PQJK est un rectangle si le triangle ABC est isocèle en B.
c) Montrer que le quadrialtère PQJK est un lsange si le triangle ABC est isocèle en A.
d) Montrer que le quadrialtère PQJK est un lsange si le triangle ABC est équilatéral.
Exercice 9
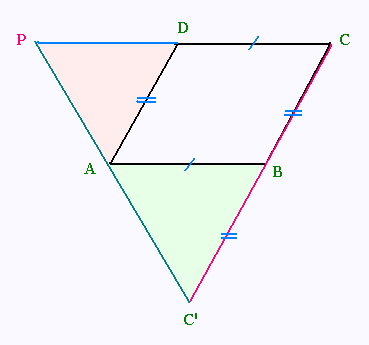
Démontrer que les triangles AC'B et ADP ont
même périmètre.
|