Maths
- 45 -
1ere Partie
2eme Partie
3eme Partie
© The scientific sentence. 2013
|
Chimie: Maths 45 Géométrie
Théorème de Thalès
Exercices de révisions
1. Théorème de Thalès direct
1ere version
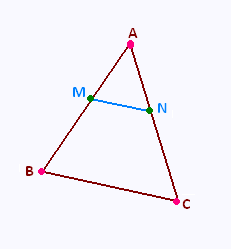 Dans un triangle ABC,
Dans un triangle ABC,
si M est un point du côté [AB], N un point du côté [AC],
et si les droites (BC) et (MN) sont parallèles,
alors :
2eme version
Pour les trois configurations suivantes:
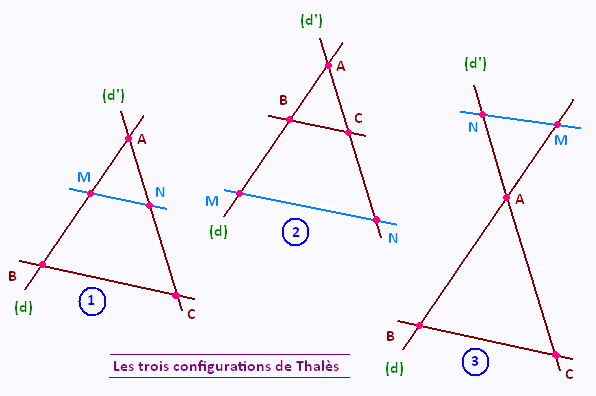
Soient (d) et (d’) sont deux droites sécantes en A,
Soient B et M deux points de la droite (d), distincts de A,
Soient C et N deux points de la droite (d’), distincts de A.
Si les droites (BC) et (MN) sont parallèles, alors :
La version 1 et la 1ere configuration de Thalès dans la version 2 sont les mêmes.
2. Réciproque du Théorème de Thalès
Pour les trois configurations de Thalès:
Soient (d) et (d’) deux droites sécantes en A,
Soient B et M deux points de (d), distincts de A,
Soient C et N deux points de (d’), distincts de A.
Exercices: Théorème de Thalès
1. Exercice résolu 1
Montrer que la configuration 2 est une configuration de Thalès.
C'est à dire qu'elle est équivalente à la configuration 1.
Les trois rapports de Thalès de la configuration 2 s'ecrivent:
En inversant ces rapports, on obtient les nouveaux rapports de Thalès, qui correspondenr à ceux de la configuration 1:
Le configurations 1 et 2 donnent les mêmes rapports. Elles sont donc équivalentes.
2. Exercice résolu 2
Montrer que la configuration 3 est une configuration de Thalès.
C'est à dire qu'elle est équivalente à la configuration 1.
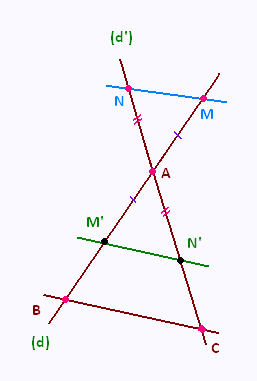
Les droites (d) et (d’) sont sécantes en A ;
B et M sont deux points de la droite (d), distincts de A ;
C et N sont deux points de la droite (d’), distincts de A ;
les droites (BC) et (MN) sont parallèles.
• Par la symétrie de centre A, on construit les points M’ et N’,
symétriques des points M et N respectivement.
Donc (M’N’) est la symétrique de (MN) par rapport à A.
Or, la symétrique d’une droite par rapport à un point est une droite qui lui est parallèle.
On en déduit que les droites (MN) et (M’N’) sont parallèles.
• De plus, on sait que les droites (MN) et (BC) sont parallèles.
Or, si deux droites sont parallèles, alors toute parallèle à l’une est parallèle à l’autre.
On en conclut que les droites (M’N’) et (BC) sont parallèles.
• M’ est le symétrique de M par rapport à A, donc AM’ = AM.
N’ est le symétrique de N par rapport à A, donc AN’ = AN.
Les segments [MN] et [M’N’] sont symétriques par rapport à A. Or,
la symétrie centrale conserve les longueurs, donc MN = M’N’.
• Dans le triangle ABC, M’ est un point du côté [AB], N’ est un point du côté [AC] et les droites (M’N’) et (BC) sont parallèles,
alors
Or, on a montré que AM’ = AM, AN’ = AN et que M’N’ = MN, donc :
Le configurations 1 et 3 donnent les mêmes rapports. Elles sont donc équivalentes.
Exercices: Réciproque du Théorème de Thalès
1. Exercice 1
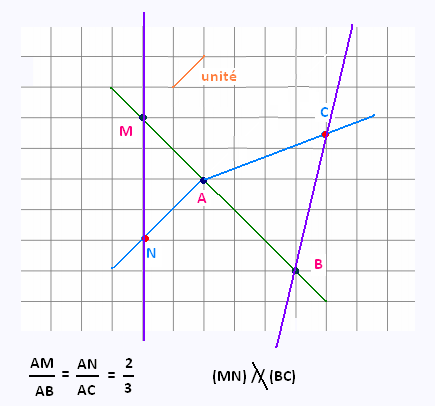
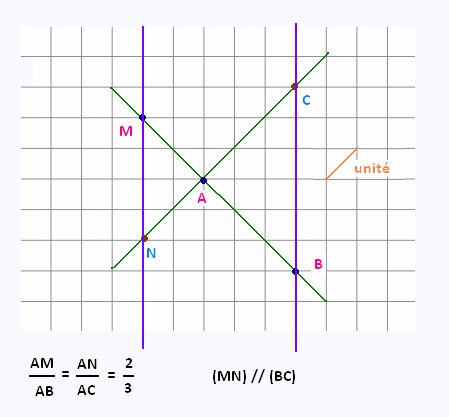
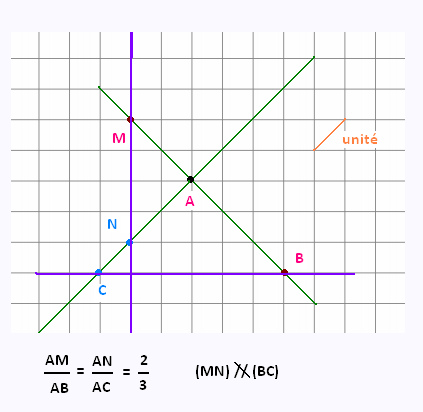
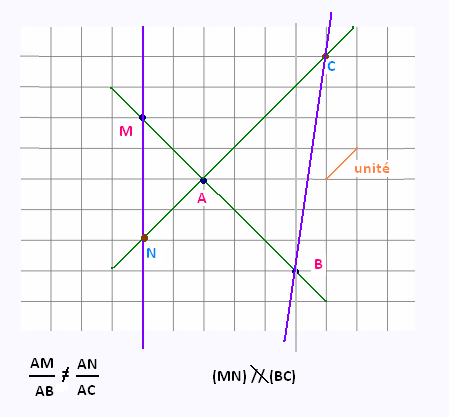
Montrer que parmi les quatres dessins suivants, un seul
correspond à une configuration de Thalès. Justifier les réponses.
|
|