Mathématiques: Géométrie
Aires et volumes

1. Les solides de bases
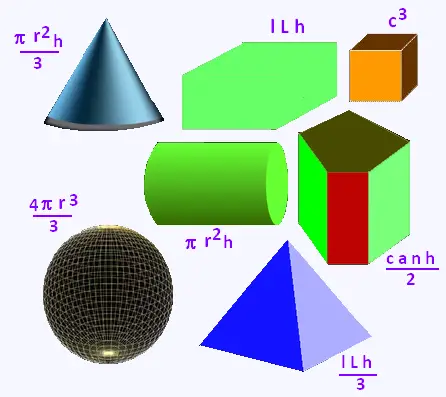
Voici les solides de bases servant à calculer le volume
de tout solide décomposable.
a) Nommer ces solides.
Toutes les dimensions des solides valent 1 unité.
b) Calculer leus volumes

2. Les rectangles d'Euclide
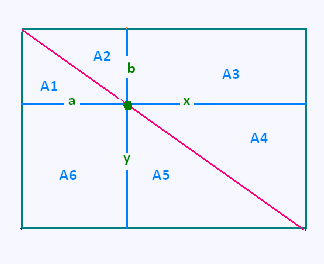
Cet exemple est extrait des "Eléments" dans le livre I, proposition 43.
Prenons un rectangle. Par un point quelconque de sa diagonale traçons
les parallèles à ses côtés. Les deux rectangles de chaque côté de la diagonale
ont la même aire.
Démontrer cette proposition à l'aide:
a) des deux triangles rectanglesde même hypoténuse qui est
la diagonale du rectangle.
b) de la trigonométrie, en considérant les tangentes
de l'angle opposé par le sommet.

3. Demi-cylindre dans un cube
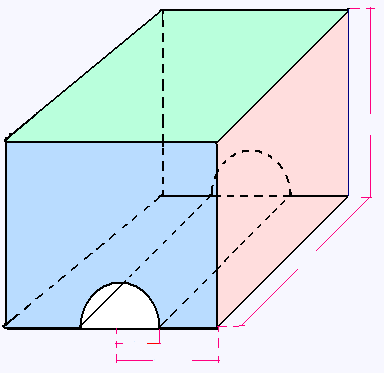
Dans un prisme à base rectangulaire, on creuse un demi-cylindre.
Choisir des mesure pour les dimensions manquantes, puis:
Calculer le volume de ce solide.
Calculer le volume du solide si l'on creuse
en entier un cylindre de même rayon.

4 Prisme pentagonal
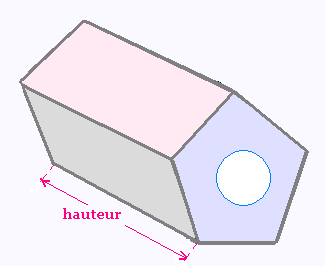
Ce prisme pentagonal a les des dimensions suivantes:
Apothème de la base = 6 cm
Côté = 4 cm et
Hauteur = 12 cm.
a) Calculer l'aire de la base pentagonale.
b) Calculer le volume de ce prisme pentagonale.
c) On creuse le long du prisme un trou de rayon égal à la moitié de l'apothème.
Quel est alors le volume du solide
obtenu?

5. Pyramide pentagone
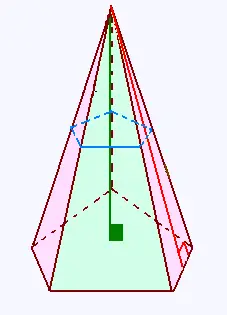
Choisir des dimensions pour l'apothème de la base, l'apothème latérale puis en
déduire la hauteur.
Choisir le côté, puis calculer le volume de cette pyramide.
Quelle serait le volume d'une pyramide obtenue
par une section de la première au niveau de la moitié de sa hauteur?

6. Pyramide carrée
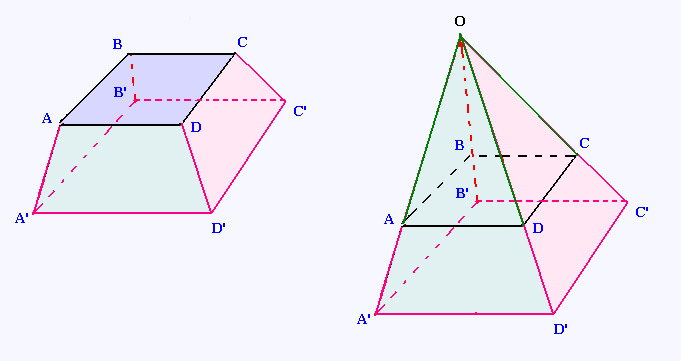
Choisir des dimensions pour les côtés de la grande base et de la petite base,
et les hauteurs des deux pyramides, puis calculer les volumes des deux
pyramides.
En déduire le volume de la pyramide tronquée.

7. Diamant
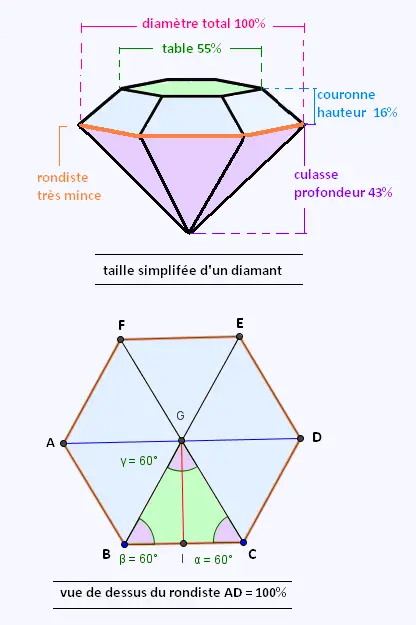
Voici une taille simple d'un diamant. Elle comporte:
• Une petite base appelé table qui mesure 55%,
• Une grande base dite rondiste de mesure 100%,
• Une couronne de mesure 16%, et
• Une culasse de mesure 43%.
Le diamètre
d'un diamant fait référence à la diagonale du rondiste.
Les pourcentages sont relatif au diamètre du diamant,
c'est à dire la taille du rondiste.
Dans la figure, le diamètre de l'aimant est égal à
la diagonale de l'hexagone.
On considère un diamant de 0.70 carat, de diamètre 5.8 mm.
a) Prouver que le triangle BCG ext équilatéral.
b) En utilant le propriété de Pythagore, déterminer
la mesure de l'apothème [IG].
c) En déduire l'aire de l'hexagone ABCDEF.
Les deux héxagones qui sont la table et le rondiste sont des
surfaces parallèles. La table est une réduction du rondiste.
d) Calculer l'aire de la table.
e) À partir de l'aire de la table et celle du rondiste,
en déduire le volume de la couronne.
f) Calculer le volume de la culasse.
g) En déduire le volume total du diamant.
La mass volumique (densité) du diamant est de 3520 kg/m3.
h) Calculer la masse du diamant.
i) Convertir cette masse en carats.
1 carat = 0,20 grammes.

8. Pyramide et sections
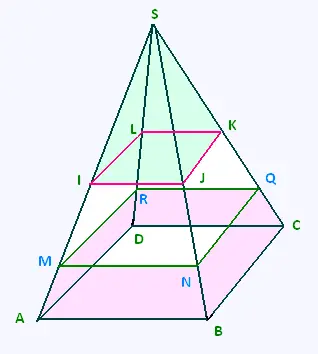
On divise une pyramide SABCD par deus sections
MNQR et IJKL et on obtient trois pyramides:
SABCD, SMNQR, et SIJKL.
La hauteur de la pyramide SMNQR est égale aux sept-neuvième de celle de la pyramide principale SABCD.
La hauteur de la pyramide SIJKL est égale aux quatre-neuvième de celle de la pyramide principale SABCD.
Le volume de la pyramide principale SABCD est égal à 900 cm3.
a) Calculer le volume des pyramides réduites
SMNQR et SIJKL.
b) En déduire le volume de la pyramide tronquée IJKL-MNQR.

9. Cône et sections
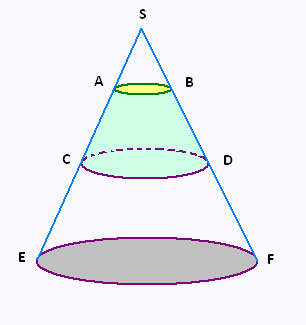
On divise un cône SEF par deus sections
CD et AB et on obtient trois cônes:
SEF, ECD, et SAB.
La hauteur du cône SCD est égale aux cinq-neuvième de celle du cône principal SEF.
La hauteur du cône SAB est égale aux deux-neuvième de celle du cône principal SEF.
Le volume du cône principal SEF est égal à 900 cm3.
a) Calculer le volume des cônes réduits
SCD, et SAB
b) En déduire le volume du cône tronqué AB-CD.

10. Volume d'un tronc de solide à bases parallèles
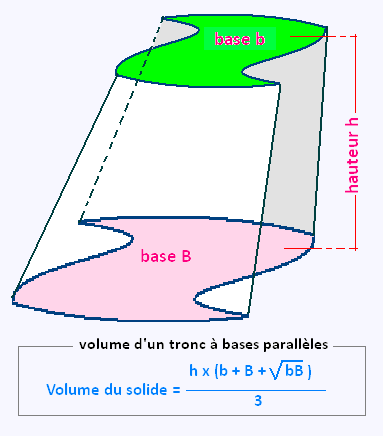
Le volume d'un tronc de solide de hauteur h et à bases b et B parallèles
est égal à :
Appliquer cette formule pour:
a) un cube,
b) un prisme à base rectangulaire,
c) un cylindre,
d) un cône, et
e) ue pyranide à base heptagonale.
|