Mathématiques 2: Géométrie
Aire et volume des solides
1. Rappel: Pyramide héxagonale
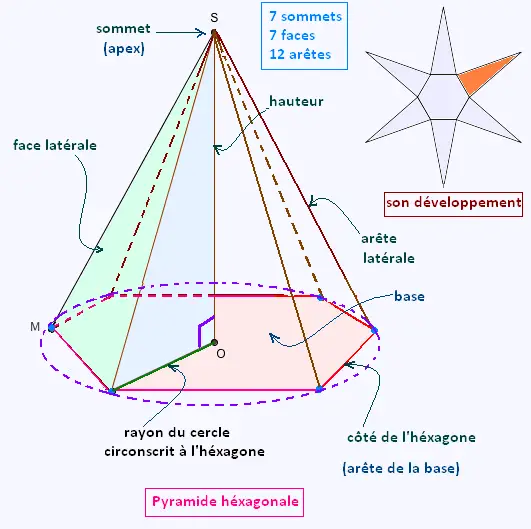
L'aire latérale est égale à 6 x l'aire d'une surface latérale.
L'aire d'une surface latérale est égale à l'aire du triangle qui la forme,
c'est à dire (apothème latéral x côté de la base)/2.
Si g est cet apothème latéral et c le côté de la base, alors l'aire
latérale de la pyramide est égale à 6 x g x c/2 = 3gc.
L'aire de base est égale à c x a x 6 /2 = 3 ac, où a est l'apothème
de la base.
L'aire totale de cette pyramide héxagonale est donc égale à:
6 x g x c/2 + c x a x 6/2 = 3c(a + g)
L'aire totale d'une pyramide n-agonale = nc(a + g)/2
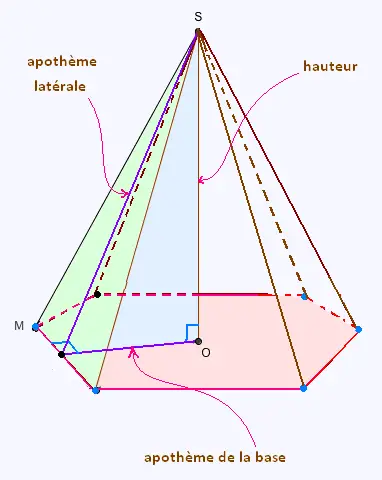
Le volume d'une pyramide est égal à l'aire de sa base fois la
hauteur de la pyramide.
Si h est la hauteur de la pyramide, alors ce volume est égal à
6 x h c a /2 = 3 h c a.
Le volume d'une pyramide n-agonale = can/2 x h
La relation de Pythagore relie l'apothème latérale "g", l'apothème de
base "a" à la hauteur h:
g2 = h2 + a2
La formule de volume ci-dessus devient:
can/2 x h = can/2 x √(g2 - a2)
Le volume d'une pyramide n-agonale = can √(g2 - a2)/2
2. Rappel: Cône droit à base circulaire
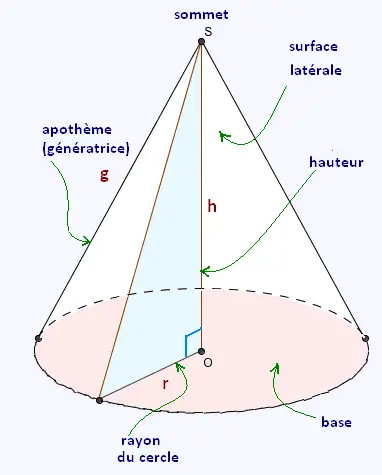
L'aire de la surface de base est égale à π r2 où
"r" est le rayon du disque qui forme cette base.
L'aire latérale du cône peut être déduite de celle d'une
pyramide avec n c = 2πr .
Ainsi, l'aire latérale du cône est égale à celle de la pyramide
n-agonale avec nc = 2πr. Donc l'aire latérale du cône est
2πr x g/2 = π r g
L'aire latérale d'un cône est égale à = π r g.
"g" est la génératrice (apothème latérale) et "r" le rayon du disque
de base.
L'aire totale du cône est égale à la somme de l'aire latérale et
de l'aire de base:
π r g + π r2 = πr(g + r)
Aire totale du cône = πr(g + r)
3. Silo cylindrique

Un silo cylindrique est composé d'une demi-sphère sur
un cylindre.
Soit un silo cylindrique de diamètre 40 dm. Son aire totale autre
que celle de sa base est égale à 6000 π dm3.
Quelle est la valeur du silo cylindrique de grains si um
m3 coûte 4$?
1. Calcul de la hauteur du cylindre
Aire de la demi-sphère + aire latérale du cylindre = 6000 π dm3.
4π x 202/2 + 2π x 20 x h = 6000 π . d'où:
h = (6000 - 2 x 202)/( 2 x 20) = (6000 - 800)/( 2 x 20) =
(300 - 40)/2 = 260/2 = 130
hauteur du cylindre = 130 dm
2. Calcul du volume du cylindre
(4/3)π 203/2 + π 202 x 130 =
π((2/3) 203 + 202 x 130) =
π(16000/3 + 400 x 130) =
1000π(16/3 +52) = 57333.33 π =
180026.67 dm3 = 180.03 m3
Volume du cylindre = 180.03 m3
3. Calcul de la valeur du cylindre
La valeur du silo cylindrique de grains est:
180.03 x 4$ = 720.11 $.
Prix des grains dans le cylindre = 720.11 $ .
4. Demi-cône sur un prisme à base triangulaire
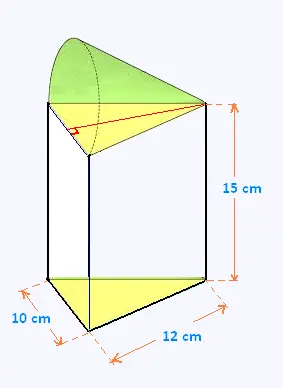
Un cône de diamètre de base d = 10 cm est coupé verticalement
en deux.
Une moitié est déposée sur une base d'un prisme à base triangulaire
dont la base du triangle isocèle de base correspond au diamètre du
cône.
Calculer l'aire totale et le volume du solide formé par le demi-cône sur de prisme
à base triangulaire de longueur 12 cm et de profondeur 15 cm.
1. Calcul de la hauteur h du cône
Le théorème de Pythagore s'ecrit:
122 = h2 + 52. D'où:
h2 = 122 - 52 = 144 - 25 = 119
h = √119 = 11 cm.
h = 11 cm.
2. Calcul de l'aire totale du solide
Aire du solide = (aire totale du cône)/2 + aire du prisme sans la base
où déposée la moitié du cône.
Aire du demi-cône A1 = (π x 5 x 12 + π 52)/2 =
(π x 5 x 12 + π 52)/2 =
85 π/5 = 133.52 cm2
Aire du prisme à base triangulaire A2 =
Aire latérale + air d'une base =
(2 x (15 x 12 ) + 10 x 15 ) + (10 x 11/2) =
(510) + (55) = 565 cm2
L'aire du solide est donc = A1 + A2 = 133.52 + 565 = 698.52 cm2
L'aire du solide est = 707.8 cm2.
3. Calcul du volume du solide
Volume du solide = (volume du cône)/2 + volume du prisme.
Volume du demi-cône V1 =
((π 52 x 11)/3)/2 = 285.59/2 = 142.80 cm3
Volume du prisme à base triangulaire V2 =
(10 x 11/2) x 15 = 825 cm3.
L'aire du solide est donc = V1 + V2 = 142.80 + 825 = 067.80 cm3
L'aire du solide est = 067.80 cm3 .
5. Boule de crème glacée sur un cornet
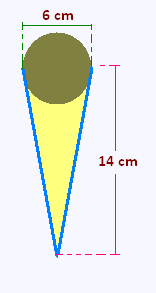
Une boule de crème lacée de rayon 3 cm est déposée sur
un cône de même rayon de base et de hauteur 14 cm.
Lorsque la boule fond, sera-t-elle entièrement contenue dans
la cornet?
Il suffit de comparer les deux volumes.
Volume de la boule de glace = Vg = (4/3)π 33 = 36 π cm3
Volume du cornet = Vc = π 32 x 14/3 = 42 π cm3
Le volume du cornet est plus grand que celui de la boule.
La boule sera entièrement contenue dans le cône après
fusion. Il restera un vide de volume égal à 42 π - 36 π = 6 π
= 18.85 cm3.
6. Espace vide dans une tente
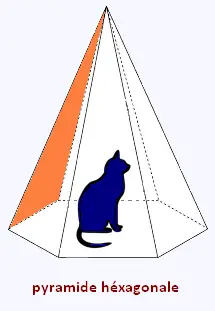
La tente est une pyramide régulière à base hexagonale de
1.5 m de côté.
À l'intérieur de la pyramide, se trouve un chat. L'espace inoccupé
est alors de 4.96 m3.
Calculer le volume occupé par le chat.
On donne l'apothème de la base a = 1.3 m, et l'aire
d'une surface latérale de la tente T = 2.2 m2
Pour trouver le volume occupé par le cube, on calcule le volume de la
pyramide puis on lui soustrait le volume inoccupé.
V(chat) = V(pyramide) - V(inoccupé).
1. Calcul de la hauteur de la pyramide:
L'aire d'une surface latérale = (côté de la base) x (apothème latéral)/2 =
c x g /2 = 2.2 m2 . D'où:
g = 2 x 2.2/c = 4.4/1.5 = 2.93 m.
g = 2.93 m.
On calcule la hauteur par la formule de Pythagone:
h2 = g2 - a2 = (2.93)2 - (1.3)2 =
6.89. d'où h = 2.62 m
h = 2.62 m.
2. Calcul du volume de la pyramide
V(pyramide) = base x hauteur/3 = (can/2) x h /3 =
(1.5 x 1.3 x 6/2) x 2.62/3 = 5.12
V(pyramide) = 5.12 m3.
Donc. V(chat) = 5.12 - 4.96 = 0.16 m3 = 160 d3
V(chat) = 160 dm3 .
7. Silo à tout usage
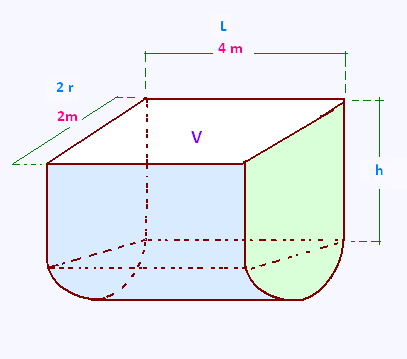
On décomposer le silo en deux parties :
La partie supérieure a la forme d'un pavé droit.
La partie inférieure a la forme d'un demi-cylindre.
Le silo a pour volume V = 3π m3.
a) Calculer la hauteur du prisme
b) En déduire l'aire totale du reservoir.
On veut peindre ce silo avec une
peinture anti-rouille qui couvre 4 m2 par litre, et
coûte 25.50 $ le litre.
c) Déterminer l'aire totale à peindre.
d) Déterminer le prix de la peinture nécessaire
pour peindre le silo des deux côtés.
Volume du demi-cylindre V1 = (π r2 x L)/2
Volume du prisme à base rectangulaire V2 = 2 r x L x h
Volume totale du contenant :
V = V1 + V2 = (π r2 x L)/2 + 2 r x L x h
= r L (π r/2 + 2 h)
Hauteur du prisme: h = (V - (π r2 x L)/2)/2rL
(1)
L'aire latérale du dem-cylindre A1 = (2πr x L +
2 πr2)/2 =
πr x L + πr2 = πr (L + r)
L'aire latérale du prisme A2 = 2r x h x 2 + h x L x 2 =
2h(2r + L)
L'aire totale du contenant est :
A = A1 + A2 = πr (L + r) + 2h(2r + L)
Avec la relation (1), on obtient:
A = πr (L + r) +
2(2r + L)((V - (π r2 x L)/2)/2rL) =
πr (L + r) +
(2r + L)(V - (π r2 x L)/2)/rL
A = πr (L + r) +
(2r + L)(V - (π r2 x L)/2)/rL
Aire totale du reservoir: A = πr (L + r) +
(2r + L)(V - (π r2 x L)/2)/rL
A = π x 1 (4 + 1) +
(2 + 4)(3π - (π x 4)/2)/4 = 5π +
6(3π - 2π)/4 = 5π + 3π/2 = 13π/2 m2
A = 13π/2 m2
On doit peindre la surface S = 2 x A.
S = 2 x 13π/2 = 13 π m2
La quantité de peinture nécessaire est:
Q = (1 L/4) x 13π = 13π/4 L = 10.21 L.
Le coût de la peinture est:
Prix = 10.21 x 25.50 = 260.36 $.
Prix = 260.36 $.
8. Culbuto
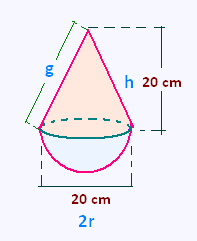
Le culbuto est utilisé comme un jouet
pour enfant qui oscille sur une
base sphérique remplie de sable.
Calculer l'aire totale et le volume
de ce culbuto.
On décompose le jouet en un cône et une demi-sphère.
1. calcul de la hauteur du cône
La génératrice g = √(r2 + h2)
2. calcul de l'air totale du culbuto
Aire latérale du cône A1 = π r g = π r √(r2 + h2)
Aire latérale de la demi-sphère A2 = 4πr2/2 = 2πr2
Aire totale du culbuto A = aire latérale du cône +
aire latérale de la demi-sphère =
π r √(r2 + h2) + 2πr2
Aire totale du culbuto =
π r √(r2 + h2) + 2πr2
A = π x 10 (100 + 400) + 2 π x 100 = 5200π cm2.
A = 5200π cm2.
3. calcul du volume du culbuto
Volume du cône V1 = πr2 x h/3
Volume de la demi-sphère V2 = (4/3)πr3/2 = (2/3)πr3
Volume du culbuto V = volume du cône +
volume de la demi-sphère = πr2 x h/3 +
(2/3)πr3
Volume du culbuto V = πr2(h + 2r)/3
V = π x 100 (20 + 20)/3 = 400π/3 cm3.
V = 400π/3 cm3.
9. Gellule
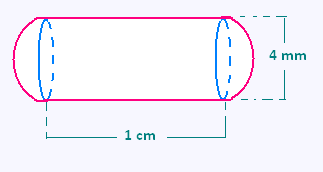
Une gélule a la forme d'un cylindre droit
avec une demi-sphère collée à
chacune de ses bases.
Calculer l'aire totale et le volume
de cette géllule.
On décomposera la géllule en un cylindre et une demi-sphère.
1. calcul de l'air totale de la géllule
Aire latérale du cylindre A1 = 2π r x h = 2π 0.2 x 1 = 0.4 π cm2.
2 x Aire latérale de la demi-sphère = Aire latérale de la sphère A2 =
4πr2 = 4π(0.2)2 = 0.16 π cm2
Aire totale de la géllule A = aire latérale du cylindre +
aire latérale de deux demi-sphères =
0.4 π + 0.16 π = 0.56 π cm2
A = 0.56 π cm2.
2. calcul du volume de la géllule
Volume du cylindre V1 = πr2 x h =
π (0.2)2 x 1 = 0.04 π cm2
Volume de deux demi-sphères V2 = 2 (4/3)πr3/2 =
(4/3)πr3 = (4/3)π (0.2)3 = (32/3000) π
= (4/375) π = 0.1067 π
Volume de la géllule V = volume du cylindre +
volume des deux demi-sphères = 0.04 π + 0.1067 π =
0.051 cm3.
Volume de la géllule V = 0.051 cm3.
10. cône circulaire droit tronqué
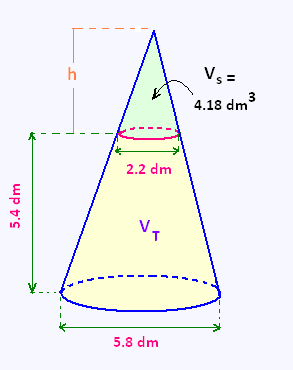
1. calcul de la hauteur du petit cône supérieur
Le volume du petit cône supérieur de hauteur "h" est:
Vs = 4.18 dm3 = π (1.1)2 x h/3 . D'où:
h = 3 x 4.18/π (1.1)2 = 3.30 dm.
h = 3.30 dm
2. calcul du volume du grand cône
V = π x (5.8/2)2 x (5.4 + 3.30)/3 =
76.62 dm3
V = 76.62 dm3
3. calcul du volume du cône tronqué
VT = V - Vs = 76.62 - 4.18
72.44 dm3
VT = 72.44 dm3 .
11. Boule lestée dans l'eau

On considère une balle lestée de 5.5 cm de rayon et un cube
de côté 10 cm rempli d'eau.
a. Calculer le volume de la balle lestée
b. Calculer le volume du cube
c. On plonge la balle dans l'eau qui déborde.
Calculer le volume d'eau restant dans le cube.
On donnera les résultats au centième près.
a. Volume de la boule Vb = (4/3)π (5.5)3 = 696.91 cm3
b. Volume du cube Vc = 10 x 10 x 10 = 1000.00 cm3.
c. Volume d'eau restant dans le cube = Vc - Vb =
1000.00 - 696.91 = 303.10 cm3.
Volume résiduel d'eau dans le cube = 303.10 cm3.
12. Boule de pétanque

Une boule de pétanque a pour diamètre 80 mm.
a. Calculer son volume.
La masse volumique de l'alliage constituant cette
boule de pétanque est de 3,50 g/cm3.
b. Calcule la masse de cette boule.
13. Ballon gonflable

Tom a acheté un ballon gonflable. Considéré comme une
sphère, le diamètre maximum de ce ballon est de 35 cm.
a. Calculer le volume maximum du ballon.
b. Combien de fois Tom doit-il souffler 500 cm3
d'air dans le ballon pour le gonfler au maximum ?
14. Moule à gâteau
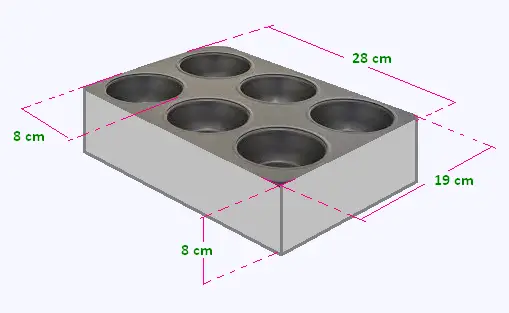
Un moule à gâteau a la forme d'un prisme droit à base
rectangulaire dans lequel on a évidé 6 cylindres identiques.
a. Détermine la surface de gâteau à recouvrir.
b. Calculer le volume de métal utilisé pour
fabriquer ce moule.
|