1. Angles:

Deux angles sont complémentaires si la somme de leurs mesures donne .... °

Deux angles sont suplémentaires si la somme de leurs mesures donne .... °

Deux angles adjacents ont le même ......, un côté ....., et sont situés de chaque côté de ce côté commun.

Les angles opposés par le sommet ont le même ..... , les côtés de l'un angle sont le prolongement des ..... de l'autre angle, ils ils sont toujours congrus.

Les angles alternes-internes sont situés de chaque côté de la ...... (alternes), et sont situés à l'intérieur des deux ...... (internes).

Les angles alternes-externes sont situés de chaque côté de la sécante (alternes), et sont situés à l'........ des deux droites (externes).

Les angles correspondants sont situés du même ..... de la sécante. Un des angles est situé à l'....... , et l'autre est situé à l'extérieur des 2 droites.

Lorsque les angles alternes-internes, alternes-externes et correspondants sont formés par deux droites ........ coupées par une ........., alors ils sont congrus.

La somme des mesures des angles ...... d'un triangle est égale à .... °

La somme des mesures des angles intérieurs d'un polygone est égale uu nombre de côté moins deux multiplié par .... °
Si n est ce nombre de côtés et S cette somme, alors S = (.... - 2)x180°.

Une droite est une .... illimité de chaque côté.
Une demi-droite est limité par un point appelé origine et ..... du côté opposé.
Un segment est une portion de droite ..... par deux extrémités.

2. Cas d'Isométrie:

Une isométrie est une transformation qui conserve les côtés et les angles.
Une translation, une rotation , une réflexion, et une homothétie de rapport 1 ou -1 sont des isométries car les mesures des côtés et des angles sont ........ .

1er cas: C-A-C:
Deux triangles qui ont un angle congru compris entre des côtés homologues congrus sont isométriques

2ème cas A-C-A:
Deux triangles qui ont un côté congru compris entre des .... homologues congrus sont isométriques.

3ème cas: C-C-C:
Deux triangles qui ont tous leurs côtés homologues congrus sont ...... .

La similitude conserve la forme.

L'homothétie est une similitude. C'est un agrandissement, une ......, ou une réplique ..... d'une figure donnée. Le coefficient d’agrandissement (ou de réduction) est appelé ..... de similitude.

Deux figures sont semblables si les angles homologues sont congrus, et les côtés ..... sont proportionnels.

3. Cas de similitude:

1er cas: C-A-C
Deux .... qui ont un angle congru compris entre des côtés homologues proportionnels sont semblables.

2ème cas: A-A (ou A-A-A)
Deux triangles qui ont deux angles ..... congrus sont semblables.

3ème cas: C-C-C
Deux triangles dont les mesures des côtés homologues sont proportionnelles sont ...... .

2. Execices

2.1. Execice 1

Tracer un cercle de centre O et deux cordes AAB et CD. Utiliser un cas de similitude pour montrer que les triangles OAB et OCD sont semblables.

2.2. Execice 2

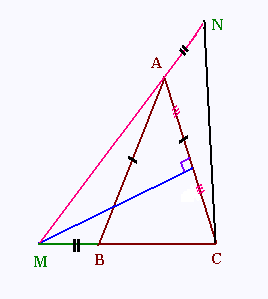
. Tracer un triangle ABC isocèle en A,
. Tracer la médiatrice de [AC]. Elle coupe la droite (BC) en M,
. Sur la droite (AM), placer Le point N est tel que AN = BM.

a) Démontrer que les triangles ABM et ACN sont isométriques.

b) En déduire que le triangle MCN est isocèle.

N.B. Pour la question b), se rappeler de la propriété du triangle isocèle suivante:

Si dans un triangle ABC la hauteur issue de A et la médiatrice de [BC] sont confondues alors il est isocèle en A.

2.3. Execice 3

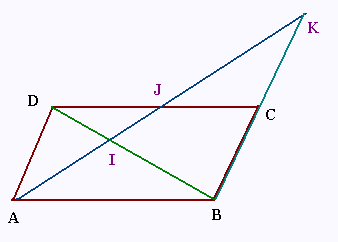
ABCD est un parallèlelogramme de largeur L et de diagonale de mesure 7 cm.

J est un point quelconque de [DC].

(AJ) coupe (BC) en K et (BD) en I. ID = 2 cm

a) Montrer que les triangles AIB et DIJ sont semblables.

b) Endéduire que DJ = 2L/5 .

c) Montrer que les triangles ADJ et JCK sont semblables.

d) AI = 3 cm, en déduire MN.

2.4. Execice 4

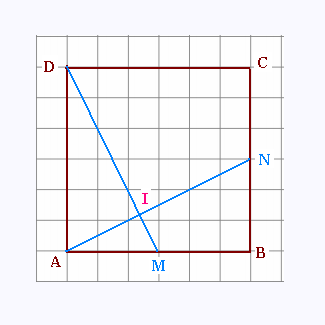
ABCD est un carré.

M et N sont les milieux respectifs de [AB] et [BC].

a) Montrer que les triangles ADM et ABN sont isométriques.

b) Montrer que l'angle I est droit.

c) En déduire que les triangles AIM et ADM sont semblables.

d) Calculer le rapport de similitude comme le coefficient d'agrandissement entre ces triangles.

e) Calculer l'aire du triangle ADM.

f) En déduire l'aire du triangle AIM.

g) Application numérique

Côté du carré c = 10 cm.

2.5. Execice 5

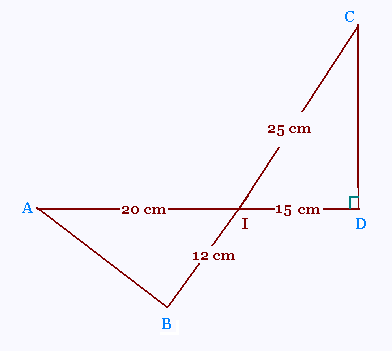
ABCD est un quadrilatère croisé rectangle en D.

IA = 20 cm, ID = 15, IC = 25 cm, IB = 12 cm

a) Montrer que les triangles AIB et DIC sont semblables,

b) réciser le rapport de similitude comme coefficient d'agrandissement.

c) Calculer CD puis AB.

d) puis l'aire du triangle CID.

e) En déduire l'aire du triangle AIB.