Mathématiques 2: Algèbre:
Exercices de révision:
Problèmes avec inégalités et inéquations
1. Comment mettre un problème en inéquation ?
Voici les 7 étapes:
• On commence par une lecture approfondie de
l'énoncé pour savoir ce que l’on recherche,
• On dessine une figure géométrique, si c'est nécessaire,
• On choisit l'inconnue,
• On met le problème en inéquation,
• On résout l'inéquation,
• On vérifie si le résultat est conforme au problème posé,
• On répond à la question avec une phrase cohérente
avec le problème.
2. Exemple
• énoncé:
Quel est le nombre maximal de petites boîtes de 2 u3
qu'on peut mettre dans une grande boîte de 32 u3 qui
est déjà remplie au 5/8 ?
• Choix de l'inconnue:
Soit x le nombre de petites boîtes.
L'espace disponible qui reste dans la grande boîte =
32 - (5/8) x 32 = 32 - 20 = 12 u3.
• Mise en inéquation:
2 x ≤ 12
• Résolution de l'inéquation:
2 x ≤ 12
(2 x)/1 ≤ 12/2
x ≤ 6.
• Réponse à la question:
Le nombre maximal de petites boîtes que l'on
peut placer dans la grande est égal à 6.
3. Exercices résolus
3.1. Compétition de lecture

William et Helena participent à un cncours de
lecture d'un roman de 800 pages.
La vitesse de lecture "A" de William est comprise entre
150 et 190 livres par jour. Celle d'Helena "B" est
comprise entre 160 et 200 livres par jour.
Au commencement de la compétition, William avait déjà lu
500 pages et Helena avait déjà lu 400 pages.
Montrer qu'Helena ne pourra jamais finir la lecture
du roman avant William.
soit x le nombre de jours que les
deux candidats doivent mettre pour finir la lecture
du roman.
On a donc:
800 = 500 + A x
800 = 400 + B x
ou
300 = A x
400 = B x
On a aussi
150 < A < 190 et
160 < B < 200
C'est à dire
150 < 300/x < 190 et
160 < 400/x < 200
On défait chaqcun des deux encadrements pour obtenir
les inégalités suivantes:
• 150 < 300/x
• 300/x < 190 et
• 160 < 400/x
• 400/x < 200
• Première inéquation:
On multiplie ses deux membres par
x qui est positif et on divise par 150 qui est positif.
Le sens de l'inéquation ne change pas. On obtient:
150 x < 300
x < 300/150
On fait un calcul similaire pour les trois autres, puis
on refait l'encadrement et on obtient:
300/190 < x < 300/150
400/200 < x < 400/160
C'est à dire
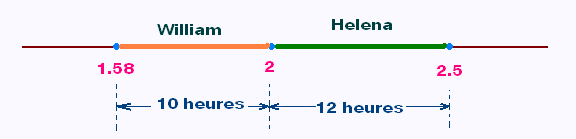
1.58 < x < 2
2 < x < 2.5
William mettra entre (1 jour + 14 heures) et (2 jours) pour finir le roman. Helena mettra entre (2 jours) et (2 jours et demi).
Willian finira le roman bien avant Helena.
En termes d'heures, on aura 10 heures pour Willian et
12 heures pour Helena:
3.2 Course en vélo
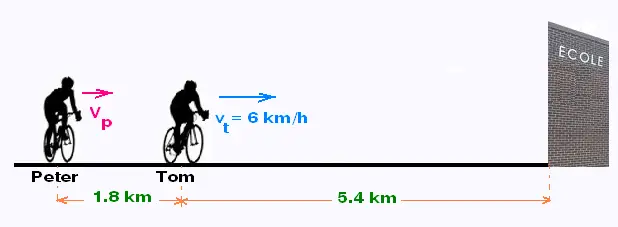
En vélo, Tom roule à une vitesse de 6 km/heure. Il
ne lui reste que 5.4 km pour arriver à l'école.
En ce momemt, Peter est à 1.80 km derrière Tom .
À quelle vitesse vp Peter doit rouler pour
rattrapper Tom avant l'école ?
Il reste à Tom t = (5.4 km)/(6 km/h) = 0.9 heures pour arriver
à l'école.
Pour rattraper Tom, Peter doit faire au plus ce temps de
0.9 heures, soit un temps inférieur à 0.9 heures.
Ainsi Peter doit parcourir au plus la distance
:
vpt = 1.80 + 5.4 = 7.2 km. Soit
t = 7.2/vp.
On a donc
t < 0.9
D'où
7.2/vp < 0.9 , ou
vp > 7.2/0.9 = 8 km/h.
Pour rattrapper Tom avant l'école, la vitesse
requise pour Peter, doit être supérieure à 8 km/h.
Interprétation
Pour le temps t = 0.9 heures:
- Tom roulera 5.4 km . Il arrivera à l'école.
- Pour Peter trois cas sont possibles:
• Si sa vitesse vp = 7.5 km/h (< 8 km/h),
il roulera 7.5 x 0.9 = 6.75 km < 7.2 km.
Il ne rattrapera donc pas Tom.
• Si sa vitesse vp = 8 km/h, il roulera
8 x 0.9 = 7.2 km.
Il arrivera donc en même temps à l'école que Tom.
• Si sa vitesse vp = 8.5 km/h (> 8 km/h),
il roulera 8.5 x 0.9 = 7.65 km > 7.2 km.
Il rattrapera Tom avant l'école.
À cette vitesse de 8.5 km/h de Peter, lorsque Tom aura
parcouru une distance x en un temps t = x/6, Peter aura
parcouru 1.8 + x pour un même temps t = (1.8 + x)/8.5.
On a donc:
t = x/6 = (1.8 + x)/8.5 , d'où
8.5 x = 6(1.8 + x) = 10.8 + 6 x
8.5 x - 6 x = 10.8
x = 10.8/2.5 = 4.32 km
Tom aura parcouru x = 4.32 km ,
Peter aura parcouru 1.8 + 4.32 = 6.12 km.
Ainsi, à cette vitesse de Peter de 8.5 km/h, Tom
sera rattrapé par Peter lorsqu'il restera
5.4 - 4.32 = 1.8 km de l'école.
Avec une vitesse vp = 10 km/h, On aura :
t = x/6 = (1.8 + x)/10 , d'où
10 x = 6(1.8 + x) = 10.8 + 6 x
10 x - 6 x = 10.8
x = 10.8/4 = 2.70 km
Ainsi, à cette vitesse de Peter de 10 km/h, Tom
sera rattrapé par lorsqu'il restera
5.4 - 2.7 = 2.7 km de l'école.
Exercice 1: Course de dromadaires

La vitesse d'un dromadaire de course peut
aller jusqu'à à 72 km/h (20 m/s) sur une
courte distance.
Deux dromadaires A et B font une course
sur 500 m.
La vitesse du dromadaire "A" est comprise entre
15 et 18 m/s. Celle de "B" est
comprise entre 16 et 19 m/s.
Au commencement de la course, le dromadare A avait
déjà parcouru une distance de 300 m, le dromadare B une distance de 100 m.
Qui gagnera la course, le dromadaire A ou le dromadaire B
?
Exercice 2

Les limites de vitesse sur les autoroutes canadiènnes
correspondent à une limite maximale de 100 km/h et
une limite minimale de 60 km/h.
100 km/h (kilomètres par heure) correspond à 60 mph (miles per hour).
Enrique est sur l'autorute. Il doit rouler à la vitesse v.
a) Donner un encadrement de v en km/h.
b) Donner un encadrement de v en mph.
Exercice 3

Roxane et Alexandre collectionnent des livres.
Alexandre possède 70 livres et achète trois livres
chaque semèstre.
Roxane possède 60 livres et achète
cinq livres chaque semèstre.
A partir de combien de jours Roxane aura-elle plus
de livres qu'Alexandre?
Exercice 4
Max a passé 2 exames. Sa moyenne est de 75 sur 100.
Quelles notes à son prochain examen lui permettront-il
d’obtenir une moyenne supérieure à 78 sur 100 ?
Exercice 5

Dans un verger, un oranger produit 60 kg d'oranges,
un citronnier produit 50 kg de citrons, par an.
À maturité, Le kilo d'oranges coûte 4 $, et le kilo
de citrons coûte 3 $.
Après la récolte, le prix d'un kilo d'orange diminue
de 3% par jour et celui des citrons augmente de 4% par
jour.
À partir de quel jour, il est profitable de
vendre des citrons plutôt que des oranges ?
Exercice 6

Le collier de Daria contient 15 graines d'açai de plus
que le double des graines de palmier pêche. Le nombre
total de ses graines compte au moins 78.
a) Combien de graines d'açaï contient le collier ?
b) Combien contient-il de graines de palmier pêche ?
Exercice 7

Un jardin ne doit pas contenir plus que
56 fleurs.
On veut planter 30 iris de plus
que le tiers des roses.
Combien d'iris et de roses doit-on planter ?
|