Mathématiques 45: Géométrie:
Rapports trigonométriques
Relations métriques dans un triangle rectangle
Exercice 1
Compléter:
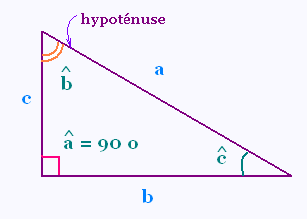
Dans ce ...... rectangle:
Le segment a : se nomme l’...
Le segment b : se nomme le côté adjacent à l’angle a.
C'est une cathète du triangle ABC.
Le segment b : se nomme le côté opposé à l’angle b.
C'est une .... du triangle ABC.
Le théorème de Pythagore est associé au .....
rectangle. Il s'ecrit:
a2 = ....2 + ...2
sinus:
sin c = côté opposé à l’angle c / ..... = c/....
cosinus:
cos c = côté .... à l’angle c / hypoténuse = .../a
tangente:
tan c = côté ..... à l’angle c / côté adjacent à l’angle c = c/b
Exercice 2
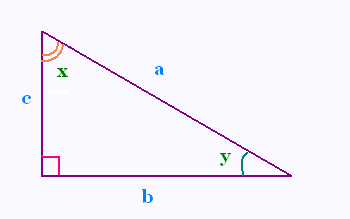
Calculer les mesures des angles x et y si:
a) a = 15 cm, b = 10 cm
b) a = 15 cm, c = 6 cm
c) b = 8 cm, c = 4 cm
Exercice 3
Construire un triangle rectangle dont le
sinus d'un angle est égal à 5/8.
Trouver la mesure manquante en utilisant le formule
de Pythagore.
b) Construire un triangle rectangle dont le
tangente d'un angle est égal à 1.
Trouver la mesure manquante.
Exercice 4
x étant un angle aingu dans un triangle rectangle.
a) Démontrer que cos2x + sin2x = 1.
b) En déduire que 1 + tan2x = 1/cos2x.
Exercice 5
Dans un triangle rectangle, il suffit de
connaître la mesure d’un côté et la mesure d’un angle
pour trouver les mesures manquantes .

a) y = 30° a = 10 cm.
calculer x, b, et c.
On remarque que, dans un triangle rectangle,
la mesure du côté opposé à un angle de 30°
est égale la moitié de la mesure de l’hypoténuse.
b) y = 45° a = 10 cm.
. calculer x, b, et c.
. Montrer que le triangle rectangle
est isocèle.
c) b = 6 cm , c = 4 cm.
Calculer a, x et y.
Exercice 6
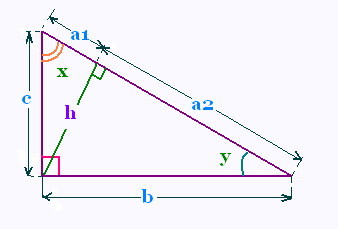
a1 = 4 cm et a2 = 6 cm.
a) En utilisant les relations métriques dans un triangle rectangle:
Calculer h , b et c
b) En utilisant les rapports trigonométriques
dans un triangle rectangle:
Calculer x et y.
Exercice 7
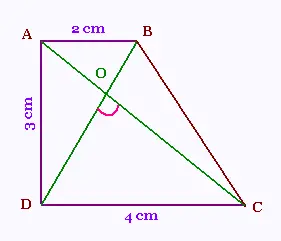
Quelle est la mesure de l'angle ∠DOC ?
Indications:
mes(∠ABD) = tan-1(3/2) = ...
mes(∠ABD) = mes(∠BDC)
(angles alternes-internes)
mes(∠ACD) = tan-1(3/4) = ...
mes(∠DOC) = 180° - mes(∠BDC) - mes(∠ACD)
= ...
Exercice 8
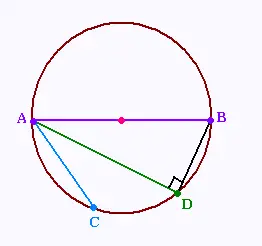
Soit un cercle de diamètre AB = 6 cm.
mes(∠CAB) = 48°.
[AD] est la bissectrice de l'angle ∠CAB.
Calculer la mesure du segment [AD] au millimètre
près?
Indications:
L'angle ∠ADB est droit, d'après la propriété
Si un point D, distinct de A et de B, est sur un
cercle de diamètre [AB], alors l'angle ∠ADB est
droit.
mes (∠DAB) = mes(∠CAB/2)
AD/AB = cos (∠DAB) =
AD = ...
Exercice 9
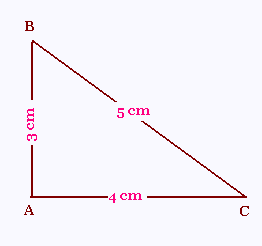
a) Vérifier que ABC est un triangle rectangle en A.
b) Calculer sin
.
c) En déduire, à 0,01 près, la mesure de l'angle
,
puis celle de l'angle .
Exercice 10
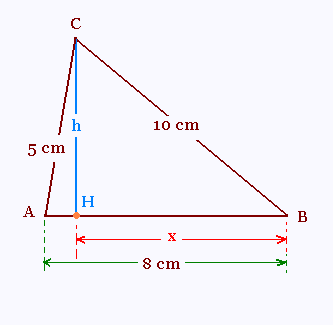
a) En utilisant la formule de Pythagore
dans deux triangles différents, calculer x, puis h.
b) Calculer, à 0.01° près les mesures des angles
,
, et
.
Indications:
h2 = 52 - (8 - x)2
h2 = 102 - x2
Donc
52 - (8 - x)2 = 102 - x2
On développe:
52 - 82 + 16 x - x2 = 102 - x2
On réduit:
52 - 82 + 16 x = 102
16 x = 102 + 82 - 52
....
On obtient:
x = ....
Exercice 11
On donne sin
= 0,985.
Sans déterminer la mesure de l'angle
,
calculer :
a) cos
, à 0.001° près.
b) tan
à 0,0001° près.
Indications:
∀, cos2()
+ sin2() = 1
Exercice 12
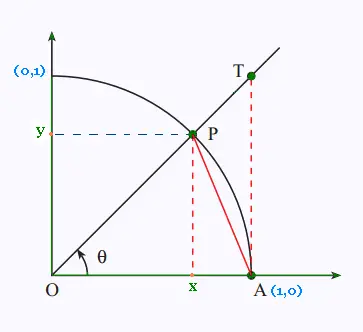
On considère un cercle de rayon R = 1 unité.
Le cerce coupe l'axe des x en A et la droite (AT) en P
de coordonnées x et y.
a) Calculer sin θ en fonction de y.
b) Calculer cos θ en fonction de x.
c) Calculer sin θ en fonction de AT.
d) Calculer cos θ en fonction de OA.
e) Calculer tan θ en fonction de x et de y.
f) Calculer tan θ en fonction de AT et de OA.
g) À partir des formules trouvées en e) et f),
en déduire le ralation entre x, y , OA et AT.
h) En utilisant la réciproque du théorème de Thalès,
montrer que la verticale passant par p et
la droite (AT) sont parallèles.
i) Calculer l'aire du triangle OAP.
j) Calculer l'aire du secteur OAP.
k) Calculer l'aire du triangle OAT.
l) En comparant les aires trouvées, déduire
l'inégalité suivante:
sin θ ≤ θ ≤ tg θ
|