Mathématiques 45: Algèbre
Systèmes de deux équations linéaires
à deux inconnues
Exercices de brevets
Exercice 1 :

Alexandre dispose d'une somme de 300 $ pour acheter des
livres qu'il choisit dans deux séries différentes A et B.
S'il choisit 4 livres de la série A et 5 livres
de la série B, il lui manque 15 $.
S'il choisit 5 livres dans la série A et 3 livres dans
la série B, il lui reste 5 $ .
a) Traduire les données par un système de deux équations.
b) Déterminer le prix d'un livre de chaque sorte.
Exercice 2 :
1. Deux nombres A et B ont pour somme 37 et pour différence 5.
Sachant que A est plus grand que B, calculer ces deux nombres.
2. Deux nombres C et D vérifient les équations suivantes :
C + D = 37
C2 - D2 = 185
a) Après avoir factorisé C2 - D2,
calculer C - D .
b) En déduire les nombres C et D .
Exercice 3 :
a) Résoudre le système
b) On désigne par x la longueur d'un rectangle et
par y sa largeur, exprimées en cm. Le périmètre de ce
rectangle est 16 cm. Si on ajoute 3 cm à la longueur
et si on double la largeur, le périmètre devient 28
cm.
Ecrire les deux équations qui correspondent à ces données
c) Déterminer la longueur et la largeur de ce rectangle.
Exercice 4 :

Dans une boulangerie, un client achète 4 baguettes et 5 croissants .
Il paie 11 $.
Un autre client achète 2 baguettes et 3 croissants . Il paie 6 $.
Quel est le prix d'une baguette ? et celui d'un croissant ?
Exercice 5 :
Le périmètre d'un rectangle est égal à 140 mm .
On double la largeur initiale et on retranche 7 mm à la
longueur initiale . Le périmètre est alors égal à 176 mm .
Quelles sont les dimensions initiales du rectangle ?
Exercice 6 :
Un élève dessine des triangles et des rectangles de façon
qu'ils n'aient aucun point commun .
Il trace ainsi 34 figures et il compte 121 sommets.
On appelle x le nombre de triangles et y le nombre de rectangles.
a) Exprimer , en fonction de x et de y , le nombre total de figures ,
puis de sommets .
En déduire un système d'équations d'inconnues x et y .
b)Résoudre ce système , et donner le nombre des triangles et celui des
rectangles
Exercice 7 :

La pièce de monnaie canadienne de 1 dollar a un
diamètre de 2.65 cm . Celle de 2 dollars a un
diamètre de 2.8 cm.
En pesant 5 pièces de 1$ et 4 de 2$ , on obtient 60.55 g.
Une seconde pesée avec 3 pièces de 1$ et 2 de 2$ donne 33.41 g.
Déterminer les masses respectives des deux pièces .
Exercice 8 :
A midi, nous étions 10 personnes au restaurant;
2 personnes ont pris le menu "A" , les autres
ont pris le menu "B" . La note s'est montée à 412 $.
Le soir, nous étions 15 personnes au même restaurant;
6 personnes ont pris le menu "A" , les
autres ont pris le menu "B" . La note s'est montée à 692 $.
Calculer le prix d'un repas "A" et le prix d'un repas "B" .
Exercice 9 :
Dans une cafétéria, un groupe d'amis a consommé trois limonades et
deux cafés. Ils ont payé 15 $ .
A la table voisine, d'autres clients ont payé 18 $ pour deux
limonades et quatre cafés.
On veut déterminer, en dollars,le prix x d'une limonade et le prix y d'un café.
a) Ecrire, en fonction de x et de y, la dépense de chacun des deux groupes.
b) Résoudre le système d'équations obtenu et donner les prix demandés.
Exercice 10 :
a) Résoudre le système
b) Au mois de novembre, un employé a travaillé 25 jours et
sa femme a travaillé 15 jours. Ils ont gagné à
eux deux 4400 $.
Au mois de décembre, ils ont travaillé chacun 20 jours et
ont gagné à eux deux 4200 $.
1) Traduire cette situation par un système de deux équations
à deux inconnues.
2) Montrer en simplifiant l'écriture du système que l'on obtient:
3) En déduire combien chacun gagne par jour de travail.
Exercice 11 :

Maria possède 45 DVD jeux vidéo en tout. Elle échange chaque jeu
de réflexion contre 4 livres et chaque jeu d'action contre
3 livres. Elle a maintenant 156 livres.
Combien de DVD jeu vidéo de chaque catégorie avais-elle
avant l'échange ?
Exercice 12 :
Sur un parking il ya des autos et des motos. Il y a
en tout 65 véhicules et on dénombre 180 roues.
Quel est le nombre de motos ?
Exercice 13 :

Un confiseur vend des chocolats au détail :
. Chaque chocolat blanc est vendu 2 $ et pèse 20 g ;
. Chaque chocolat noir est vendu 3 $ et pèse 35 g.
On paye 84 $ pour 900 g.
Déterminer le nombre de chocolats de chaque sorte.
|
Solution:
montrer
|
masquer
|
|
Exercice 14 :
Sébastien dispose d'une somme de 224 $ pour acheter des
livres qu'il choisit dans deux collections
différentes A et B.
S'il choisit 4 livres de la collection A et 5 livres de la collection B,
il lui manque 3 $.
Il choisit alors 5 livres de la collection A et 3 livres de la collection B ;
il lui reste 2 $ .
1) Traduire les données par un système de deux équations à deux inconnues.
2) Calculer le prix d'un livre de chaque collection.
Exercice 15 :
Au moment de la rentrée, Judith a payé 50 $ pour l'achat de 4
cahiers et de 3 classeurs.
Dans le même magasin, Gabriel a acheté 3 cahiers et 4 classeurs identiques
à ceux de Judith. Il a payé 48 $.
Après avoir traduit la situation sous la forme d'un système
de deux équations du premier degré à deux
inconnues, calculer, dans ce magasin, le prix d'un cahier et celui d'un classeur.
Exercice 16 :
1) Résoudre le système :
2) Un camion transporte 20 caisses de masses différentes:
les unes pèsent 28 kg, les autres 16 kg.
Sachant que la masse totale de ces caisses est 416 kg,
combien y a-t-il de caisses de chaque catégorie ?
Exercice 17 :
Si on laisse couler la première fontaine pendant quatre
heures et la seconde pendant trois heures, la
quantité d'eau recueillie au total est de 55 litres.
Si on laisse couler la première fontaine pendant trois
heures et la seconde pendant quatre heures, la
quantité d'eau recueillie au total est de 57 litres.
1) On désire calculer le débit, en litre par heures, de
chacune des fontaines.
Pour cela, on admet que les renseignements précédents sont
traduits par le système de deux équations à
deux inconnues :
où x est le débit horaire de la première fontaine et y est le
débit horaire de la seconde fontaine.
Résoudre le système et indiquer le débit horaire de chacune
des deux fontaines.
2) Sachant que ce bassin peut contenir 320 litres,
combien faudra-t-il de temps pour le remplir, si les
deux fontaines coulent ensemble pendant le même temps ?
Exercice 18 :
1) Résoudre le système :
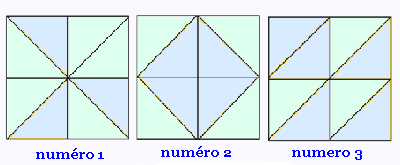
2) On fabrique des badges à l'aide de triangles,
tous de même forme, dont certains sont vert,
et les autres sont bleus.
Les triangles de même nature sont tous au même prix.
Le badge n°1 revient à 20,50 $ ; le badge n°2
revient à 22 $.
A combien revient le badge n° 3 ?
Exercice 19 :
1) Résoudre le système d'équations d'inconnues x et y :
2) Max achète 24 livres. Des livres de Mathématiques à 40 $ l'un
et des livres de Physique à 35 $ l'un.
Max ayant versé 1000 $, on lui rend 90 $.
a) Mettre le problème en équations.
b) Combien Max a-t-il acheté de livres de chaque sorte ?
Exercice 20 :

Alexandre et Roxane sont allées passer quelques jours aux États
puis en Australie.
De retour, Alexandre constate qu'il lui reste 3 USD et 5 AUD
pour lesquels on lui rembourse 8.00 CAD.
Quant à Roxane, il lui reste 12 USD et 3 AUD pour lesquels on
lui rembourse 14,50 CAD.
Trouver la valeur en dollar canadien (CAD) d'un dollar américain
(USD) et d'un dollar australien (AUD), en traduisant les données
par un système d'équations que l'on résoudra.
Exercice 21 :
À la plage il est possible de louer à la journée des
chaises longues et des parasols.
Pour une journée, la famille A loue 2 parasols et 4
chaises longues pour 84 $ alors que la famille B loue 3
parasols et 5 chaises longues pour 114 $.
On veut déterminer le prix de la location à
la journée d'un parasol et celui de la location à la journée d'un
chaise longue.
Mettre le problème en équation et le résoudre.
Exercice 22 :

Un fleuriste compose des bouquets de deux sortes
avec des iris et des oeillets.
Les uns sont formés de trois iris et de dix oeillets
et sont vendus 43 $, les autres sont formés de deux
iris et de cinq oeillets et sont vendus 25 $.
Déterminer le prix d'un iris et le prix d'un oeillet.
Exercice 23 :
1) Résoudre le système suivant :
2) Résoudre l'inéquation
4 x - 5 ≤ 10 x + 1.
Représenter en couleur les solutions sur une droite graduée.
3) Le nombre 4 vérifie-t-il l'équation
x2 – 5 x = 4 ? Indiquer les calculs.
On ne cherchera pas à résoudre
cette équation.
Exercice 24 :

1) Résoudre le système :
2) Pour un parc floral, un paysagiste achète un lot
de 35 plantes constitué de rosiers à 28 $ le pied et
d'azalées à 52 $ pièce.
Le montant de la facture correspondant à cet achat est 1 316 $.
Déterminer le nombre de pieds de rosiers et le nombre
d'azalées achetés.
Exercice 25 :
1) Résoudre le système suivant, d’inconnues x et y :
2) Si x désigne le prix d'un article, exprimer en fonction de x le
prix de cet article après une baisse de 20 %.
3) Pour l'achat d'un livre et d'un stylo, la dépense est de 35 $.
Après une réduction de 20 % sur le prix
du livre et de 30 % sur le prix du stylo, la dépense n'est que de 26 $.
Calculer le prix d'un livre et celui d'un stylo avant la réduction.
Exercice 26 :
1) Résoudre le système :
2) Rachel et Ben disposent à eux deux d'une somme de
450 $.
Rachel dit à Ben : " Si je te donne
50 dollars, mon avoir sera alors le double du tien."
En désignant par x l'avoir initial de Rachel et par y
celui de Ben , mettre le problème en équation et
déterminer l'avoir initial de chacun des
deux personnages.
Exercice 27 :
Robin achète 2 compas et 3 équerres, il paie 77 $.
Tom achète 3 compas et 4 équerres, il paie 111 $.
Quel est le prix d'un compas ? Quel est le prix d'une équerre ?
Exercice 28 :
Soit le système :
l) En considérant chacune des équations comme une équation
de droite, résoudre graphiquement le système précédent
(on se placera dans un repère orthonormé et on prendra pour
unité graphique 0.5 cm).
2) Résoudre le système précédent par le calcul.
3) Traduire le dialogue suivant par un système d'équations :
• Lothaire : "Si je doublais mon nombre de CD, j'en aurais 7 de plus que toi."
• Daria : "Si nous en achetions encore 2 chacun, nous en aurions 24 au total."
On désignera par x le nombre de CD de Lothaire et par y celui de Daria.
4) Quel est le nombre de CD possédés par chacun des deux enfants ?
Exercice 29 :
Pour la rentrée scolaire, Cristina achète quatre
cahiers et un classeur pour 32,50 $.
Elena achète trois cahiers et deux classeurs pour 42,50 $.
1) Ecrire un système d'équations traduisant les
données précédentes.
2) Résoudre ce système pour trouver le prix d'un cahier
et d'un classeur.
Exercice 30 :
Diego se rend à la papeterie avec Fernand.
Diego achète un cahier et un classeur ; il paie 11 dollars.
Fernand achète 3 cahiers et 4 classeurs ; il paie 40 dollars.
Traduire cette situation à l'aide d'un système de deux
équations à deux inconnues et en déduire le prix
d'un cahier et celui d'un classeur.
Exercice 31 :

Une régate, ou course de voiliers, est organisée à Ottawa.
Deux types de voiliers participent à la régate :
. les "A2" qui ont à bord deux personnes,
. les "A1" qui sont manœuvrés par une seule personne.
On compte au départ de la régate 48 voiliers et 80 personnes.
l) Si x est le nombre des "A2" au départ et y le nombre des "A1",
traduire les données par un système de 2 équations à 2 inconnues.
2) Quel est le nombre de voiliers de chaque catégorie ?
Exercice 32 :
1) Résoudre le système de deux équations suivant :
2) Pour l'organisation d'une fête à l'école,
un commerçant fournit 20 packs de boissons gazeuses et 30
packs de jus.
A la livraison, il remet sa facture d'un montant de
1800 F payable après la fête.
Après la fête, le commerçant récupère les invendus :
7 packs de boissons gazeuses et un pack de jus
dont le montant s’élève à 250 F.
a) Quel est le prix d'un pack de boisson gazeuse ?
b) Quel est le prix d'un pack de jus ?
Exercice 33 :

1) Résoudre le système :
2) Un fleuriste propose des roses, des tulipes
et des glaïeuls.
Malia achète 8 roses et 5 tulipes pour 77,50 $
Sasha achète 5 roses et 8 tulipes pour 65,50 $.
a) Quel est le prix d'une rose ?
b) Quel est le prix d'une tulipe ?
c) Sachant qu'un glaïeul coûte 8 $ et une rose
7,50 $, Michael pourra-t-elle acheter 13 roses et 19
glaïeuls avec 250 $ ?
d) Amanda, qui a 200 $, décide d'acheter 15 roses,
combien pourra-t-il acheter de glaïeuls avec
l'argent qui lui restera ?
Exercice 34 :
1) Résoudre le système :
2) Pour un spectacle, un comité d'entreprise a acheté 14
places pour ses adhérents. Pour cela, il a dépensé 1060 $.
Une place "adulte" coûte 90 $ et une place "enfant" coûte 50 $.
Déterminer le nombre de places "adulte" et le nombre de
places "enfant" achetées par le comité.
Exercice 35 :
Deux carnets de tickets de transport plein tarif et trois
carnets de tickets tarif réduit coûtent 167 $.
Un carnet de tickets de transport plein tarif et deux carnets
de tickets tarif réduit coûtent 96 $.
Calculer le prix d'un carnet plein tarif et le prix d'un carnet
tarif réduit.
Pour cela, vous appellerez x le prix d'un carnet plein tarif
et y celui d'un carnet tarif réduit, puis vous mettrez ce
problème en équation.
Enfin, vous vérifierez votre réponse par un calcul que
vous écrirez sur la copie.
Exercice 36 :
Au théâtre, le prix normal d'un billet d'entrée est de 120 $.
1) Certains spectateurs peuvent bénéficier d'une réduction de
20%. Combien paient-ils leur entrée?
2) Un groupe de 25 personnes va au théâtre, certaines parmi
elles paient 120 $ et d'autres 96 $.
Sachant que pour les 25 entrées le groupe a payé 2784 $,
trouver le nombre de billets à 120 $ et le
nombre de billets à 96 $ vendus à ce groupe.
Exercice 37 :
Au Café de la Place, Robert et ses amis ont commandé
trois cafés et deux chocolats pour la somme de 42 $.
Edward et ses camarades ont payé, eux, 56 $ pour deux cafés
et quatre chocolats.
En écrivant, puis en résolvant un système de deux équations
à deux inconnues, trouver le prix d'un café
et le prix d'un chocolat.
Exercice 38 :
Au cinéma East-Wood, le prix d'un billet est de 22 $ pour un adulte
et de 14 $ pour un étudiant.
11 personnes assistent à la projection d'un film et paient 230 F.
Parmi ces 11 personnes, combien y a-t-il d'étudiants ?
Exercice 39 :
Un confiseur prépare deux types de paquets comportant
des chocolats fins et des pâtes de fruits.
Dans le paquet de type 1, qu'il vend 102,50 $,
il place 25 chocolats et 10 pâtes de fruits.
Dans le paquet de type 2, qu'il vend 82,50 $,
il place 15 chocolats et 20 pâtes de fruits.
Calculer le prix d'un chocolat et celui d'une pâte de fruits.
Pour résoudre ce problème, on désignera par x le prix d'un
chocolat et par y celui d'une pâte de fruits.
Exercice 40 :

À l'occasion de la fête des grand-mères, un enfant
achète deux bouquets chez un fleuriste.
Le premier bouquet, composé d'une rose et de cinq marguerites,
coûte 17 francs.
Le deuxième bouquet, composé de trois roses et de deux marguerites,
coûte 25 francs.
Calculer le prix d'une rose et le prix d'une marguerite.
Exercice 41:

Michael et James ont réservé des places sur les mêmes gradins pour
la coupe du monde de soccer.
Michael a réservé 3 places pour le match d'ouverture et 4 places
pour un match de quart de finale. Il a payé
5 300 $.
James a réservé 6 places pour le match d'ouverture et 5 places pour
un match de quart de finale. Il a
payé 8 020 $.
On note x le prix d'une place pour le match d'ouverture et
y le prix d'une place pour un match de quart de finale.
1. Traduire les renseignements ci-dessus par un système
de deux équations à deux inconnues.
2. En résolvant ce système, déterminer le prix d'une place pour
le match d'ouverture et le prix d'une place pour un match de quart
de finale.
Exercice 42:
À la solderie, Maria a acheté 4 draps de bain et 5
gants de toilette. Elle a payé seulement 110 $.
Anna a pris ce qui restait: 6 draps de bain et 4 gants
de toilette. En payant 172 $, Anna a pensé qu'il y a une erreur.
1. En appelant x le prix d'un drap de bain et y le prix
d'un gant de toilette, traduire cette situation par
un système de 2 équations à 2 inconnues.
2. Résoudre ce système.
3. Anna a-t-elle raison de penser qu'il y a une erreur ?
Exercice 43:

1. Résoudre le système suivant :
2. Pour un concert de jazz, les places valent 42 $
ou 80 $.
Une association a acheté 27 places pour un montant de 1514 $.
Combien de places de chaque sorte l'association a-t-elle achetées ?
Exercice 44
Eliza dit à Calos : "Si tu me donnes ... billes, j'en aurai
autant que toi."
Carlos réplique : "Si je t'en donne ... tu en auras .... fois
plus que moi."
1. Observer la mise en équations de ce problème :
Soit e le nombre de billes d'Eliza, et c le
nombre de billes de Carlos :
Recopier l'énoncé du problème en le complétant par les
nombres qui manquent.
2. Calculer le nombre de billes d'Eliza et de Carlos.
Exercice 45

1. Résoudre le système suivant :
2. À une buvette, la consommation de trois cafés
et d'une limonade coûte 23,50 $.
La consommation de sept cafés et de quatre limonades
coûte 79 $.
Déterminer le prix d'un café et le prix d'une limonade.
Exercice 46
1. Résoudre le système :
2. Montrer que ce système permet de répondre à la
question posée dans le problème suivant :
La coopérative d'un collège a organisé une séance
de cinéma; il y a eu 250 entrées et la recette totale
est de 49375 ¢
Le prix d'une place est de 3 $ pour un adulte et de 1.75 $
pour un enfant.
Quel est le nombre d'adultes et le nombre d'enfants ayant
assisté à cette séance ?
Exercice 47
Un confiseur prépare deux sortes de boîtes
comportant des tuiles en chocolat et des macarons
à la pâte d'amande.
Dans le paquet de la première sorte, il place 20 tuiles et
15 macarons : ce paquet sera vendu 96 $.
Dans le paquet de la deuxième sorte, il place 10
tuiles et 25 macarons : ce paquet sera vendu 90 $.
Calculer le prix d'une tuile et celui d'un macaron.
Exercice 48
Pour équiper une salle de réunion, M. Planck
achète des chaises et des tabourets.
Chaque chaise coûte 200 $ et chaque tabouret 80 $.
Il paie au total 6 000 $.
Il a acheté 5 chaises de moins que de tabourets.
Quel est le nombre de chaises et le nombre de
tabourets achetés par M. Planck ?
Exercice 49
La recette d'un match s’élève à 36500 $.
Le prix d'une place en tribune est 50 $ et celui d'une place en
"populaire" est 30 $.
Sachant que 1000 spectateurs ont payé leur place pour ce match,
déterminer le nombre de spectateurs qui ont acheté une place
en tribune et le nombre de ceux qui ont acheté une place
en "populaire".
Exercice 50
George a acheté cinq tee-shirts et deux jeans : il a payé 680 $.
Frank a acheté quatre tee-shirts, un jean et un blouson qui coûte
600 $ : il a payé 1060 $.
Quel est le prix d'un tee-shirt ? Quel est le prix d'un jean ?
Exercice 51
1. Voici un système de deux équations du premier
degré à deux inconnues x et y :
Démontrer, en le résolvant, que ce système admet
pour solution x = 28 et y = 12.
2. Un groupe de 40 personnes s’est inscrit pour une
visite guidée à Montréal.
Ce groupe est composée de x adultes et de y enfants.
Les adultes paient 90 $ et les enfants 50 $. Le responsable
du groupe a remis 3120 $ à l’organisateur du circuit.
Combien y a-t-il d’adultes et d’enfants dans ce groupe ?
Exercice 52
Dans un musée, le prix d’entrée est de 50 $ pour un
adulte et 35 $ pour un enfant.
1. Calculer le pourcentage de réduction consenti sur
le prix d’entrée "enfant" par rapport au prix
d’entrée "adulte".
2. Un dimanche, le musée a reçu 125 personnes et
a fait une recette de 5125 $.
Calculer le nombre d’adultes et le nombre d’enfants
qui ont visité le musée ce dimanche là.
Exercice 53
Trois cahiers et un stylo coûtent 57 $.
Cinq cahiers et trois stylos coûtent 107 $.
Calculer le prix d'un cahier et le prix d'un stylo.
Exercice 54
a) Résoudre le système suivant :
b) Dans un parc zoologique, la visite coûte 30 $
pour les adultes et 18 $ pour les enfants.
A la fin d'une journée, on sait que 630 personnes ont
visité le zoo et que la recette du jour est de 14 220 $.
Parmi les personnes qui ont visité le zoo ce jour-là,
quel est le nombre d'enfants ?
quel est le nombre d'adultes ?
Exercice 55
Un premier bouquet de fleur est composé de 3
iris et 4 roses jaunes, il coûte 48 $.
Un second bouquet est composé de 5 iris et de 6
roses jaunes, il coûte 75 $.
On appelle x le prix en dollars d'un iris et y le prix
en dollars d'une rose jaune.
Ecrire un système d'équations traduisant les données
de ce problème et calculer le prix d'un iris et celui
d'une rose jaune.
Exercice 56
Un cirque propose deux tarifs d'entrée :
un pour les adultes et un pour les enfants.
Un groupe de trois enfants avec un adulte paie 290 $.
On peut traduire ces données par l'équation à deux inconnues :
3 x + y = 290
Un autre groupe de 5 enfants avec quatre adultes paie 705 $.
1. Ecrire alors une deuxième équation et résoudre le système
obtenu de deux équations à deux inconnues.
2. Donner le prix d'une entrée pour un enfant et celui
d'une entrée pour une adulte.
Exercice 57

1. Résoudre le système de deux équations à deux inconnues suivant :
2. Pour financer une partie de leur voyage de fin d'année,
des élèves de troisième vendent des gâteaux qu'ils ont
confectionnés eux-même.
Un même jour ils ont vendu 15 tartes, les unes aux myrtilles et
les autres aux pommes.
Une tarte aux myrtilles est vendue 4 dollars et une tarte aux
pommes 2 dollars.
La somme encaissée ce jour là est 42 dollars.
Apres avoir mis le problème en équation, déterminer combien
ils ont vendu de tartes de chaque sorte.
Exercice 58
Une élève de CP fait des courses pour elle et ses camarades :
- La première fois, elle achète 5 crayons et 2 gommes pour 10,90 $.
- La seconde fois elle achète 8 crayons et 3 gommes pour 17,20 $.
En utilisant un système d’équations, aider l’élève de CP
à retrouver le prix de chaque article.
Exercice 59

On considère le système suivant :
1) Le couple (2,0,5) est-il solution de ce système ?
2) Résoudre le système d'équations.
3) A la boulangerie, David achète 2 croissants et 3
pains au chocolat : il paie 5,50 $.
Nancy achète 3 croissants et 1 pain au chocolat
et paie 4,05 $.
Quel est le prix d'un croissant ?
Quel est le prix d'un pain au chocolat ?
Exercice 60
1) Résoudre le système suivant :
2) Une balade d'une heure en mer est proposée à
deux groupes de touristes.
Le premier groupe, composé de 8 adultes et de 3 enfants,
paie 39,50 $.
Le second, composé de 7 adultes et de 9 enfants, paie 50,50 $.
Quel est donc le prix d'un ticket pour un adulte ? Pour un enfant ?
Exercice 61
1) Résoudre le système :
2) Pour classer des photos, un magasin propose deux types de
rangement : des albums ou des boîtes.
Colin achète 6 boîtes et 5 albums et paie 57 $ ;
Brook achète 3 boîtes et 7 albums et paie 55,50 $.
Quel est le prix d'une boîte ?
Quel est le prix d'un album ?
Exercice 62
Trouver un nombre fractionnaire x/y sachant que
a)Si on ajoute 8 au numérateur et si on retranche 9
du dénominateur, on trouve 3.
b)Si on retranche 1 du numérateur tout en
ajoutant 17 au dénominateur, on trouve 0.1.
Exercice 63
a) Ecrire x2 - y2 sous la forme d'un produit de facteurs.
b) Soient deux entiers positifs x et y dont la différence des carrés
vaut 144 et dont la somme vaut 24.
En déduire leur différence.
c) Connaissant maintenant la somme et la différence de ces deux nombres,
donner la valeur de chacun d'entre eux.
Exercice 64
Soit un rectangle de longueur L et de largeur l mesurées en mètres.
a) Donner son aire en fonction de L et de l.
b) On sait que si on augmente sa longueur de 9 m et que si
l'on diminue sa largeur de 3 m, l'aire de ce
rectangle est inchangée.
Traduire cette affirmation par une relation entre L et l.
On notera (1) le résultat obtenu.
c) On sait que si on diminue sa longueur de 7 m et si l'on
augmente sa largeur de 4 m, l'aire de ce
rectangle est inchangée.
Traduire cette affirmation par une relation entre L et l.
On notera (2) le résultat obtenu.
d) En résolvant le système de deux équations (1) et (2)
à deux inconnues L et l trouver la largeur et la
longueur de ce rectangle.
Calculer son aire.
e) Calculer, alors, la longueur de la diagonale de ce rectangle.
En donner la valeur exacte, puis à l'aide de
votre calculatrice la valeur approchée par défaut à 1 mm près.
Exercice 65
Le soir du deuxième tour, le candidat battu s'adresse au vainqueur:
"Avec chacun deux millions de voix en moins, je faisais les trois
quarts de votre score ; mais vous avez réalisé aujourd'hui la moitié
du total que nous aurions fait à nous deux avec chacun deux millions
de voix en plus."
Quel est, en millions de voix, le score des deux candidats?
Indications:
x = 14 et y = 18.
Exercice 66
Les deux exercices sont indépendants.
a) Résoudre le système :
b) Une île sur 18 de l'archipel des Bermudes est
habitée contre une île sur 11 pour l'archipel des
Bahamas.
Il y a 50 îles habitées sur un total de 690 îles
pour l'ensemble des deux archipels.
Calculer le nombre d'îles habitées pour chacun d'eux.
Indications:
x = 20, y = 30.
|