Mathématiques 23 Géométrie
Triangles rectangles et cercles
Exercice 1
Compléter:
On dit ... circonscrit au triangle et
cercle inscrit dans un triangle.
On appelle cercle ..... à un triangle
le cercle qui passe par les trois sommets de ce triangle.
Son centre est le point d'... des médiatrices des
trois côtés de ce triangle.
Les propriétés directes d'une figure géométriques proviennent
de la nature de cette figure:
Par exemple, une propriété directe d'un triangle rectangle est que
ce triangle possède un angle .... .
Les propriétés réciproques d'une figure géométrique pouvent la nature de cette figure.
Par exemple, les propriétés réciproques d'un triangle isocèle montre que ce triangle est ... .
Exercice 2
Il s'agit des propriétés des triangles rectangles et cercles.
Compléter:
2.1. Propriétés:
P1.
Si un triangle est rectangle, alors le milieu de l’.....
est le centre de son cercle circonscrit.
P2.
Si un angle BAC est ...., alors A appartient au cercle de
diamètre [BC].
P3.
Si un triangle est rectangle, alors la longueur de la
.... issue de l’angle droit est la moitié de celle de
l’hypoténuse.
2.2. Propriétés réciproques:
PR1.
Si un triangle est défini par le diamètre d’un cercle et
un autre point du cercle, alors ce triangle est .... .
PR2.
Si le sommet A d’un angle appartient au .... de
diamètre [BC] alors l’angle BAC est droit.
PR3.
Si dans un triangle, la médiane issue d’un sommet à une
longueur égale à la ... du côté opposé
alors ce triangle est rectangle en ce sommet.
Exercice 3
Il s'agit des propriétés du triangle isocèle.
Compléter:
Compléter:
2.1. Propriétés
P1.: Si ABC est isocèle en A alors, la hauteur issue de A,
la bissectrice de A, la ... issue de A, la médiatrice de [BC] sont confondues.
P2.: Les deux angles à la base d'un triangle isocèle ont même ... .
2.2. Propriétés réciproques
PR1.:
Si un triangle a ses angles à la base .... alors il est isocèle.
PR2.:
Si dans un triangle ABC la médiane issue de A et la ... de [BC] sont confondues alors il est isocèle en A.
PR3. :
Si dans un triangle ABC la médiane issue de A et la ... de l'angle A sont confondues alors il est isocèle en A.
PR4. :
Si dans un triangle ABC la médiane et la ... issues de A sont confondues alors il est isocèle en A.
PR5. :
Si dans un triangle ABC la hauteur issue de A et la médiatrice de [BC] sont ... alors il est isocèle en A.
PR6. :
Si dans un triangle ABC la hauteur issue de A et la bissectrice de l'angle A sont confondues alors il est ... en A.
PR7. :
Si dans un triangle ABC la bissectrice de l'angle A et la médiatrice de [BC] sont ... alors il est isocèle en A.
PR8.: Si dans un triangle ABC, deux angles à la base ∠B et ∠C ont même mesure, alors ce triangle est ... en A.
3. Exercice:
cercle ciconscrit au triangle rectangle
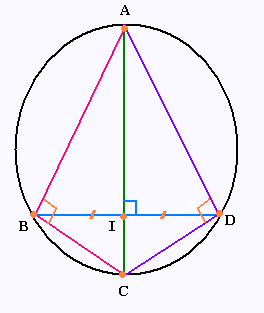
A et C sont deux points diamétralement opposés
sur le cercle.
B est un point quelconque sur le cercle.
D est le symétrique de B par rapport à la
droite (AC).
a) Montrer que le triangle ABC est rectangle en B.
b) Montrer que D est sur le cercle.
 Solutions Solutions
|