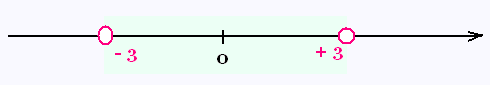Mathématiques 45: Algèbre
Racine carrée
Valeur absolue et radicaux

La fonction radical prend du positif et donne du positif.

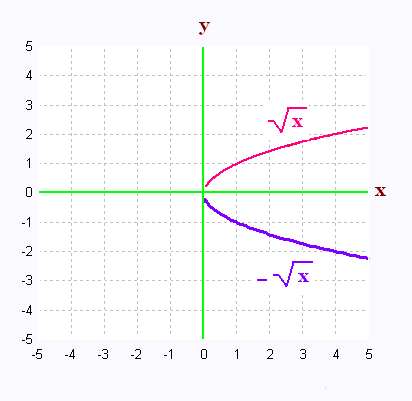
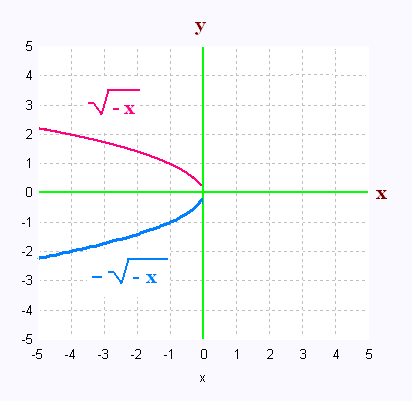
1. Graphique des fonctions radicales de base

Voici les graphes de :

$\sqrt{x}$,$- \sqrt{x}$,$\sqrt{- x}$, et $- \sqrt{- x}$

Le radical prend du positif et donne du positif. Ainsi

La racine carrée $\sqrt{x}$ est toujours positive.

Le radicande dans $\sqrt{x}$ est toujours positif.

Le nombre réel sous le radical ne peut être que positif. $\sqrt{x}$ est toujours positif.

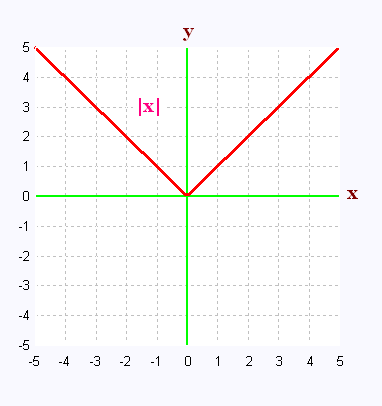
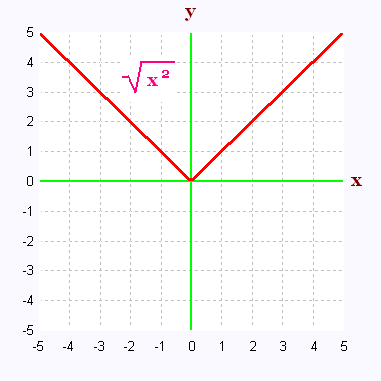
La valeur absolue d'un nomre réel est égale à la racine carré de son carré. $\sqrt{x^2}$ = |x|.

2. Relation entre $\sqrt{x^2}$ et |x|

Nous savons que la valeur abslue d'un réel x est difini par:

$|x| = \begin{cases} + x & \text{si $x $ } \ge 0 \\ - x & \text{si $x $ } \lt 0 \\ \end{cases}$

L'expression $\sqrt{x^2}$ doit s'ecrire:

$\sqrt{x^2}$ = $(\sqrt{x})^2$ = |x|

Exemple:

$\sqrt{16}$ = 4 (d'après la définition du radical $\sqrt{ }$).

$\sqrt{(+ 4)^2}$ = $\sqrt{16}$ = 4. C'est à dire |+ 4|.

$\sqrt{(- 4)^2}$ = $\sqrt{16}$ = 4. C'est à dire |- 4|.

3. Exemples d'quations radicales absolues

3.1. Exemple 1

x² < 9

x² est ≥ 0 et 9 ≥ 0.

On peut donc les mettre sous des radicaux sans changer le sens de l'inégalité.

Nous avons:

$\sqrt{x^2} \lt \sqrt{9} \\ \sqrt{x^2} = |x| \\ \sqrt{9} = 3. \\ \text{ }\\ \text{On obtient:}\\ \\ \text{ }\\ \text{|x| } \lt 3 \;\; \begin{cases} + x \lt 3 & \text{si $x $ } \ge 0 \\ - x \lt 3 & \text{si $x $ } \lt 0 \\ \end{cases} \\ \text{ }\\ \text{ou}\\ \text{|x| } \lt 3 \;\; \begin{cases} x \lt 3 & \text{si $x $ } \ge 0 \\ x \gt - 3 & \text{si $x $ } \lt 0 \\ \end{cases}$

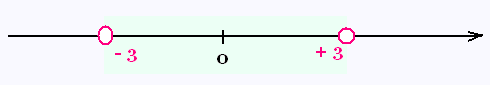
L'ensemble des solutions est donc S = ]- 3, + 3[.

3.2. Exemple 2

x² ≥ 16

x² est ≥ 0 et 9 ≥ 0.

On peut donc extraire leur racine carré sans modifier le sens de l'inégalité.

Nous avons:

$\sqrt{x^2} \ge \sqrt{16} \\ \sqrt{x^2} = |x| \\ \sqrt{16} = 4. \\ \text{ }\\ \text{On obtient:}\\ \\ \text{ }\\ \text{|x| } \ge 4 \;\; \begin{cases} + x \ge 4 & \text{si $x $ } \ge 0 \\ - x \ge 4 & \text{si $x $ } \lt 0 \\ \end{cases} \\ \text{ }\\ \text{ou}\\ \text{|x| } \ge 4 \;\; \begin{cases} x \ge 4 & \text{si $x $ } \ge 0 \\ x \le - 4 & \text{si $x $ } \lt 0 \\ \end{cases}$

L'ensemble des solutions est donc S = ]- ∞ - 4] ∪ [+ 4, + ∞[ .

3.3. Exemple 3

$\sqrt{x^2}$ > - 2

ou

|x| > - 2

$\color{green}{\text{ Sans faire de calcul; la valeur absolue de n'importe quel }}\\ \color{green}{\text{ nombre réel est positive, donc à fortiori supérieure à }} \\ \color{green}{\text{ - 2. Ainsi l'ensemble des solutions de l'inéquation est }} \\ \color{green}{\text{ l'ensemble de tous les nombres réels.}}$

$\text{|x| } \;\; \begin{cases} + x \gt - 2 & \text{si $x $ } \ge 0 \\ - x \gt - 2 & \text{si $x $ } \lt 0 \\ \end{cases} \\ \text{ }\\ \text{ou}\\ \text{|x| } \;\; \begin{cases} x \gt - 2 & \text{si $x $ } \ge 0 \;\; (1)\\ x \lt + 2 & \text{si $x $ } \lt 0 \;\; (2) \\ \end{cases}$


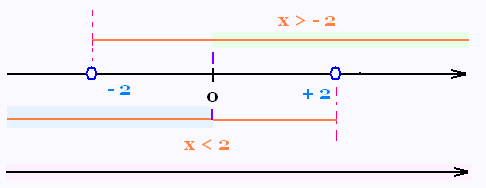
Pour la première inéquation, l'ensemble des solutions est: [0, + ∞[

Pour la deuxième inéquation, l'ensemble des solutions est: ]- ∞, 0]

L'ensemble des solutions est donc S = ]- ∞ 0] ∪ [0, + ∞[ (tous les nombres réels).

3.4. Exemple 4

$\sqrt{x^2}$ < - 2

ou

|x| < - 2

$\color{green}{\text{ Sans faire de calcul; la valeur absolue de n'importe quel nombre }}\\ \color{green}{\text{ réel est positive, donc jamais inférieure à - 2. Ainsi l'ensemble }} \\ \color{green}{\text{ des solutions de l'inéquation est vide. L'inéquation n'a pas de solutions. }}$


$\text{|x| } \;\; \begin{cases} + x \lt - 2 & \text{si $x $ } \ge 0 \\ - x \lt - 2 & \text{si $x $ } \lt 0 \\ \end{cases} \\ \text{ }\\ \text{ou}\\ \text{|x| } \;\; \begin{cases} x \lt - 2 & \text{si $x $ } \ge 0 \;\; (1)\\ x \gt + 2 & \text{si $x $ } \lt 0 \;\; (2) \\ \end{cases}$

Pour la première inéquation, l'ensemble des solutions est l'ensemble vide {}.

Pour la deuxième inéquation, l'ensemble des solutions est l'ensemble vide {}.

L'ensemble des solutions est donc S = {}. L'inéquation n'a pas de solutions.

4. Exercices

Trouver l'ensemle des solutions des inéquations suivantes:

$\text{1.}\; \sqrt{x} \gt - 8 \\ \text{2.} \;x^2 \lt 81 \\ \text{3.}\;\sqrt{x} \lt 8 \\ \text{4.}\;\sqrt{x} \gt 8 \\ \text{5.}\; x^2 \gt 47 \\ \text{6.}\;|x| \gt - 12 \\ \text{7.}\;\sqrt{x} \ge - 2 \\ \text{8.}\;|x| \lt - 12 \\ \text{9.}\;\sqrt{x^2} \ge - 5 \\ \text{10.}\sqrt{x} \lt 0 \\ $