Mathématiques 45: Algèbre
L'extraction d'une racine carrée
Méthode arithmétique

1. La méthode

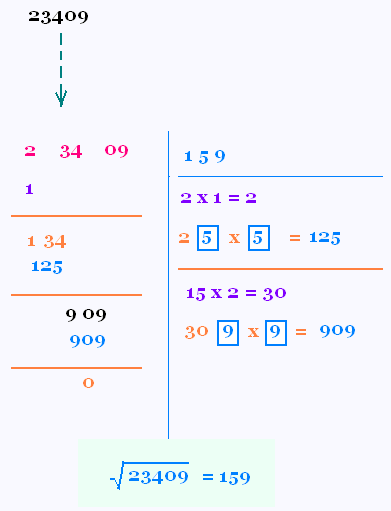
La démarche ressemble à celle de la division euclidienne des entiers naturels.
Le radicande à la place du dividende, et la racine à la place du diviseur.

On présente ici une méthode pour extraire la racine carré d'un nombre. Cette méthode peut s'appliquer pour n'importe quel nombre.



L'exemple considéré est le nombre 23409.

1. On partage le radicande en tranches de deux chiffres en partant de la droite. (la dernière tranche peut donc avoir 1 ou 2 chiffres).

2. On cherche le plus grand carré inférieur à la première tranche (celle de l'extrême gauche) et on inscrit sa racine à la place du diviseur.
Ici, c'est 1.

3. On retranche ce carré de la première tranche et on abaisse la tranche suivante.
On obtient alors ici 134

4. On double la racine obtenue (placée au diviseur) et on l’inscrit à la place du quotient.
On obtient ici 1 x 2 = 2

5. À droite de ce nombre, on place (comme chiffre d'unités) le plus grand chiffre □ de sorte que le produit par □ soit inférieur au nombre obtenu au dividende.
Ici □ vaut 5 parce que 2□ x □ qui est 25 x 5 = 125 (6 c'est trop, et 4 c'est peut).

6. On inscrit 5 à gauche du diviseur et on soustrait le produit obtenu dans la partie dividende.
Ici, on obtient 134 - 125 = 9

7. On abaisse la tranche suivante (la dernière), on obtient 909.

8. comme au 4), on double la racine obtenue (placée au diviseur) et on l’inscrit à la place du quotient.
On obtient ici 15 x 2 = 30.

9. Comme au 5) à droite de ce nombre, on place (comme chiffre d'unités) le plus grand chiffre □ de sorte que le produit par □ soit inférieur au nombre obtenu au dividende (909)
Ici □ vaut 3 parce que 30□ x □ qui est 303 x 3 = 909 (4 c'est trop, et 2 c'est peut).

10. Comme au 6), on inscrit 3 à gauche du diviseur et on soustrait le produit obtenu dans la partie dividende.
On trouve 0. On arrête.

Ainsi

√23409 = 153.

Remarque:

Si le reste n'est pas nul, on inscrit la tranche 00 au dividende, on place une virgule au diviseur et on continue comme pour les étapes précédentes.

On peut laisser les virgules à la fin. On inscrit des tranches 00 et on continue le calcul. Ainsi, à la fin de l'opération, le nombre de chiffres décimaux est égal aux nombres de tranches ajoutées.

2. Exercices

Extraire, à la main, les racines carrées des nombres suivants:

a) N = 2025
b) N = 321489
c) N = 1328.6025
d) N = 120585