Maths
- 45 -
Racine carrée
Exercices
Calculateurs
© The scientific sentence. 2013
|
Mathématiques 45: Algèbre
Racine carrée
Inéquations avec des radicaux
On présente ici les exemples types.
1. Racine carrée et nombres positifs
a) 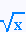 ≥ 7 ≥ 7
Le radicande doit être positif ou nul.
C'est à dire x ≥ 0
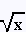 ≥ 0 et
7 ≥ 0 ;
On peut donc élever au carré les deux membres de
l'inégalité. On obtient: ≥ 0 et
7 ≥ 0 ;
On peut donc élever au carré les deux membres de
l'inégalité. On obtient:
(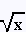 )2 ≥ 72 )2 ≥ 72
C'est à dire:
x ≥ 49
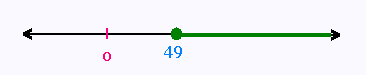
Les solutions sont donc tous les réels ≥ 49
avec la contrainte x ≥ 0. Ce qui revient
à tous les x ≥ 49
L'ensemle des solutions est S = [49, + ∞[
b)
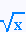 < 7 < 7
Le radicande doit être positif ou nul.
C'est à dire x ≥ 0
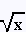 ≥ 0 et
7 ≥ 0 ;
On peut donc élever au carré les deux membres de
l'inégalité. On obtient: ≥ 0 et
7 ≥ 0 ;
On peut donc élever au carré les deux membres de
l'inégalité. On obtient:
(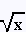 )2 < 72 )2 < 72
C'est à dire:
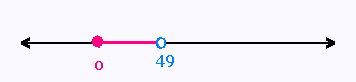
x < 49
Les solutions sont donc tous les réels < 49
avec la contrainte x ≥ 0.
L'ensemle des solutions est S = [0, + 49[
c)
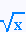 > 7 > 7
Le radicande doit être positif ou nul.
C'est à dire x ≥ 0
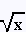 ≥ 0 et
7 ≥ 0 ;
On peut donc élever au carré les deux membres de
l'inégalité. On obtient: ≥ 0 et
7 ≥ 0 ;
On peut donc élever au carré les deux membres de
l'inégalité. On obtient:
(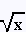 )2 > 72 )2 > 72
C'est à dire:
x > 49
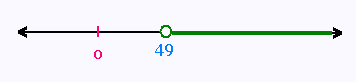
Les solutions sont donc tous les réels ≥ 49
avec la contrainte x ≥ 0. Ce qui revient
à tous les x > 49
L'ensemle des solutions est S = ]49, + ∞[
2. Racine carrée et nombres négatifs
a)
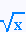 > - 5 > - 5
Le radicande doit être positif ou nul.
C'est à dire x ≥ 0
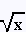 ≥ 0 et
- 5 ≤ 0 ;
On ne peut donc pas élever au carré les deux membres de
l'inégalité. ≥ 0 et
- 5 ≤ 0 ;
On ne peut donc pas élever au carré les deux membres de
l'inégalité.
Il suffit juste de regarder l'équation pour détérminer
les solutions.
N'importe quel nombre positif qu'on place sous le radical,
l'inéquation reste vraie.
Les solutions sont donc tous les réels ≥ 0 .
L'ensemle des solutions est S = R+ = [0, + ∞[

b)
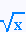 < - 5 < - 5
Le radicande doit être positif ou nul.
C'est à dire x ≥ 0
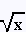 ≥ 0 et
- 5 ≤ 0 ;
On ne peut donc pas élever au carré les deux membres de
l'inégalité. ≥ 0 et
- 5 ≤ 0 ;
On ne peut donc pas élever au carré les deux membres de
l'inégalité.
Il suffit juste de regarder l'équation pour détérminer
les solutions.
D'après la définition de la racine carrée, 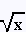 > 0. N'importe quel nombre positif qu'on place sous le radical,
l'inéquation reste fausse. > 0. N'importe quel nombre positif qu'on place sous le radical,
l'inéquation reste fausse.
Il n' y pas de solutions pour ce genre d'équation .
L'ensemle des solutions est S = Φ = {}
|
|