Maths
- 2 -
Statistiques
© The scientific sentence. 2010
|
|
Mathématiques 2: Probabilités
diagramme de Venn
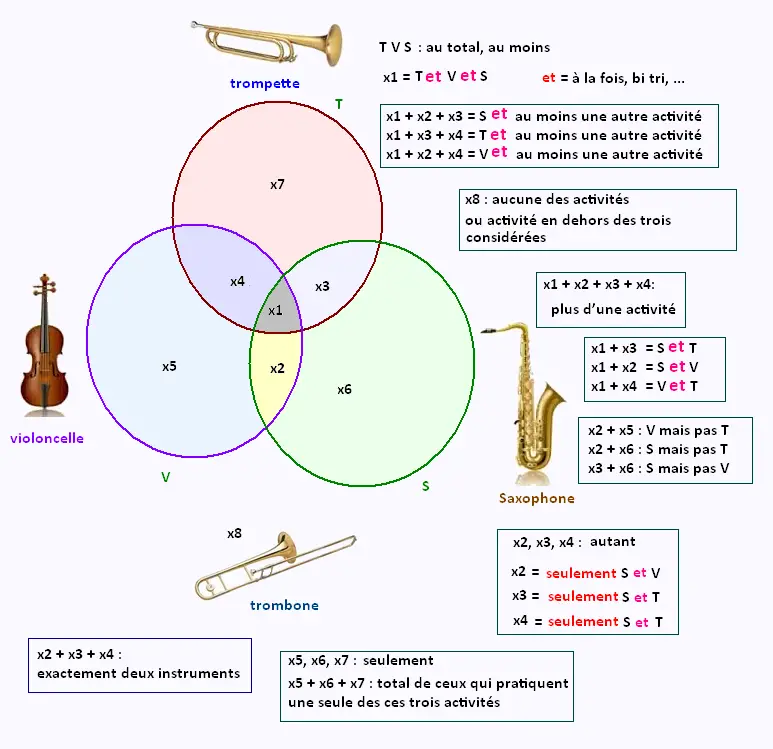
1. Les effectifs
On considère les 4 instruments de musique suivantes:
Le violoncelle,
La trompette,
Le saxophone, et
La trombone.
Le violoncelle est un instrument à cordes, les trois autres sont des instruments à vent.
Au total, M musiciens jouent des différents
instruments.
1. Quel est le nombre des musiciens qui jouent :
• du violoncelle
x1 + x2 + x4 + x5
• de la trompette
x1 + x3 + x4 + x7
• du saxophone
x1 + x2 + x3 + x6
2. Quel est le nombre des musiciens qui jouent :
• seulement du violoncelle
x5
• seulement de la trompette
x7
• seulement du saxophone
x6
3. Quel est le nombre des musiciens qui jouent :
• du violoncelle et de la
trompette
x1 + x4
• de la trompette et du saxophone
x1 + x3
• du saxophone et du violoncelle
x1 + x2
• au moins du saxophone et du violoncelle
x1 + x2
4. Quel est le nombre des musiciens qui jouent :
• de plus d'un instrument
x1 + x2 + x3 + x4
• aussi bien (à la fois) de la trompette que
du saxophone et du violoncelle
x1
5. Quel est le nombre des :
• musiciens qui ne jouent ni de la trompette ni
du saxophone, ni du violoncelle
x8
6. Quel est le nombre des musiciens qui :
• jouent de la trompette et au moins un autre instrument
x1 + x7 + x3 + x4
• au total jouent de la trompette
x1 + x7 + x3 + x4
7. Formuler la proposition:
• Il y a autant de musiciens qui jouent du violoncelle et de
la trompette que des musiciens qui jouent du violoncelle et du saxophone
x1 + x4 = x1 + x2
8. Quel est le nombre des musiciens qui jouent :
• du violoncelle mais pas de la
trompette
x2 + x5
• de la trompette mais pas du saxophone
x4 + x7
• du saxophone mais pas du violoncelle
x3 + x6
9. Quel est le nombre des musiciens qui jouent :
• du violoncelle et de la trompette
x1 + x4
• de la trompette et du saxophone
x1 + x3
• du saxophone et du violoncelle
x1 + x2
10. Quel est le nombre des musiciens qui jouent seulement:
• du violoncelle et de la trompette
x4
• de la trompette et du saxophone
x3
• du saxophone et du violoncelle
x2
11. Quel est le nombre des musiciens qui jouent :
• d'un seul de ces instruments
x5 + x6 + x7
• de plus d'un instrument
x1 + x2 + x3 + x4
• au moins du violoncelle
x1 + x2 + x4 + x5
• au moins du saxophone
x1 + x2 + x3 + x6
• au moins de la trompette
x1 + x3 + x4 + x7
12. Quel est le nombre des musiciens qui jouent :
• de ces instruments sauf du violoncelle
x3 + x6 + x7
• de ces instruments sauf de la trompette
x2 + x6 + x5
• de ces instruments sauf du saxophone
x4 + x5 + x7
13. Quel est le nombre des musiciens qui jouent autant:
• du violoncelle que du saxophone
x2
• du violoncelle que de la trompette
x4
• de la trompette que du saxophone
x3
14. Formuler la proposition :
• Il y a autant de musiciens qui jouent du violoncelle que
de la trompette et du saxophone
x1 + x2 + x4 + x5 = x1 + x3
• Il y a autant de musiciens qui jouent de la trompette que
du saxophone et du violoncelle
x1 + x3 + x4 + x7 = x1 + x2
• Il y a autant de musiciens qui jouent du saxophone que
de la trompette et du viloncelle.
x1 + x3 + x2+ x6 = x1 + x4
15. Formuler la proposition:
• Il y a 4 fois plus de musiciens qui jouent du saxophone
et du violoncelle que de musiciens qui jouent du saxophone et
de la trompette
x1 + x2 = 4(x1 + x3)
• Il ya autant de musiciens qui jouent du saxophone que
de musiciens qui jouent du violoncelle et au moins d'un autre instrument.
x1 + x2 + x3 + x6 = x1 + x2 + x4
2. Les probabilités
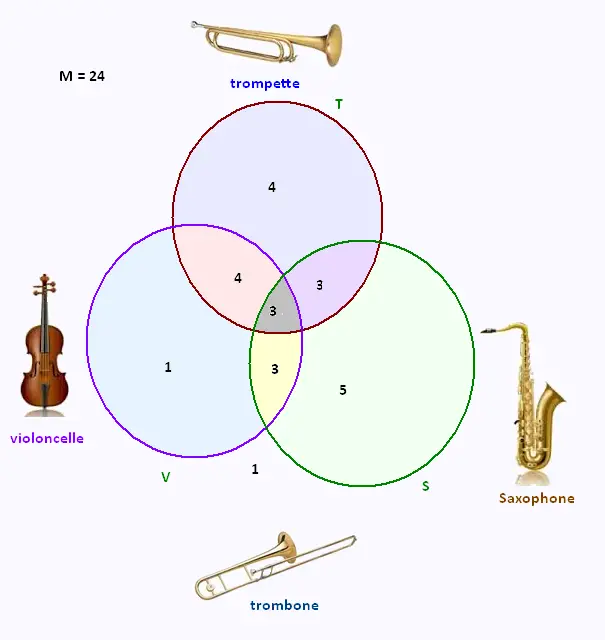
Si on choisit un musicien au hasard parmi les M musiciens
considérés, quelle est la probabilité que le musicien ou
la musiciènne:
• joue uniquement de la trompette?
• préfèré le violoncelle?
• préfèré uniquement (le seul) le violoncelle?
• joue exactement des deux instruments ?
• préfère la trombone ou ne joue d'aucun instrument?
• ne joue à aucun instrument?
• joue au violoncelle ou à la trompette?
• joue d'un seul instrument?
• joue d'au moins un instrument?
• joue du saxophone?
• joue du saxophone?
|
|