Mathématiques 2: Probabilités
arbre de probabilité

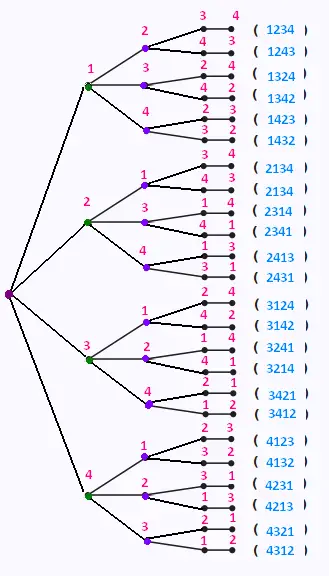
On dispose, dans une urne, des quatre chiffres: 1, 2, 3, et 4.

On prend au hasard un chiffre, puis un deuxième, ensuite un troisième, et enfin un quatrième.

Combien y a-t-il de nombres de 4 chiffres qu'on peut construire avec ces quatre chiffres ?

La représentation par un diagramme en arbre donne toutes les combinaisons possibles (tous les nombres possibles).

Il y a 24 combinaisons possibles.

• Chacune des possibilités à une probabilité de (1/4) x (1/3) x (1/2) x (1/1) = 1/24 de se produire. Total = 24 x (1/24) = 1.

• Avec 6 tirages, la probabilité d'avoir un nombre de dizaine de mille égale 3 est 6/24 = 1/4.

• Avec 12 tirages, la probabilité d'avoir un nombre inférieur à 3000 est 12/24 = 1/2.

• Avec 12 tirages, la probabilité d'avoir un nombre supérieur à 3000 est égale à 1 - P(nombre < 3000) 1 - 12/24 = 1/2.