Maths
- 2 -
Statistiques
© The scientific sentence. 2010
|
|
Mathématiques 2: Statistiques:
Classes et histogrammes
1. Définitions
Une série statistique ou série de données est appelé
aussi distribution statistique ou
distribution de données.
Certaines distributions de données peuvent
être très longues. Ainsi, il est nécessaire de condenser
ces données sous une forme de classes plus favorable
à l’analyse statistique.
Lorsqu’une distribution comporte un nombre de données
répétées, il convient de les placer dans un tableau à
données condensées.
Les tableaux de distribution et les
diagrammes sont des outils qui permettent
de mieux comprendre une étude statistique du phénomène
considéré.
2. Données condensées
Exemple

On ceuille 24 mandarines et on les pèse
une par une.
Nous avons la liste de données qui
représente les masses des mandarines en
grammes:
102, 100, 105, 103, 103, 105, 105, 98, 99, 105,
102, 99, 101, 103, 102, 103, 101, 102, 102, 99,
102, 102, 98, 102.
Le tableau des données condensées:
| masse (g) | effectif |
| 98 | 2 |
| 99 | 3 |
| 100 | 1 |
| 101 | 2 |
| 102 | 8 |
| 103 | 4 |
| 105 | 4 |
La première colonne indique le caractère de l’étude
ou les données, c'est à dire la masse.
La deuxième colonne indique le nombre de fois
que la donnée se répète, c'est à dire l'effectif.
24 est le nombre total de données.
3. Données groupées en classes
3.1. Définitions
Lorsque les données de la distribution sont
nombreuses, on les divise en classes.
On ecrit la liste des données en ordre croissant,
en rassemblant les effectifs, puis on regroupe toutes ces données en classes.
Pour déterminer les classes:
- On calcule l’étendue : max – min
- On détermine le nombre de classes
Il n’y a pas de règle stricte pour fixer le
nombre de classes, on compte habituellement entre
5 et 10 classes.
- On étermine la largeur des classes. C'est
le rapport entre l’étendue et le nombre de classes retenues. Toutes les classes doivent avoir la même largeur.
Chaque classe débute par un crochet fermé et se termine par un crochet ouvert. Le crochet fermé indique un
élément inclus, le crochet ouvert indique un
élément exclus,
- On regroupe dans un tableau de données en classes.
Lorsque les données sont groupées en classes:
- Les modes sont remplacés des classes modales. Il s’agit des classes possédant le plus d’effectifs.
- On estime la médiane au milieu de la classe médiane.
- On estime la moyenne à la somme des produits des milieux des classes par leur effectif /
total des effectifs
Le milieu d'une classe est égal à la demi-somme de
son élément inclus + son élément exclus.
Le milieu de chacune classe est égal au milieu de sa classe
précédente augmenté de la largeur de la classe.
3.2. Exemple

On ceuille de nouveau 30 mandarines, puis on
les pèse au centième près. Nous avons:
102.45, 100.00, 103.95, 105.22, 103.28, 103.28, 105.45, 105.10, 99.55, 105.22,
102.25, 99.10, 101.95, 104.25, 105.05, 100.05, 100.85, 102.00, 103.00, 101.95,
102.45, 102.25, 99.55, 102.24, 102.12, 104.35, 105.65, 103.65, 105.10,104.25.
Le tableau I représente les données condensées:
| Tableau I | |
| masse (g) | effectif |
| 99.10 | 1 |
| 99.55 | 2 |
| 100.00 | 1 |
| 100.05 | 1 |
| 100.85 | 1 |
| 101.95 | 2 |
| 102.00 | 1 |
| 102.12 | 1 |
| 102.24 | 1 |
| 102.25 | 2 |
| 102.45 | 2 |
| 103.00 | 1 |
| 103.28 | 2 |
| 103.65 | 1 |
| 103.95 | 1 |
| 104.25 | 2 |
| 104.35 | 1 |
| 105.05 | 1 |
| 105.10 | 2 |
| 105.22 | 2 |
| 105.45 | 1 |
| 105.65 | 1 |
| Total | 30 |
|
|
L'étendue est égale à:
105.65 - 99.10 = 6.55
On va prendre 5 classes.
La largeur , ou l'amplitude est donc égale à 6.55/5 = 1.31.
On augmente légèrement l'amplitude de cet intervalle
afin de s'assurer que la plus grande valeur soit incluse
dans la dernière classe. Donc, on peut la hausser à 1.35.
Voici les 5 classes:
[99.10, 100.45[, [100.45, 101.80[, [101.80, 103.15[, [103.15, 104.50[, [104.50, 105.85[.
Groupées dans un tableau (Tableau II) avec leurs effectifs respectifs:
| Tableau II | |
| classes (g) | effectif |
| [99.10, 100.45[ | 5 |
| [100.45, 101.80[ | 1 |
| [101.80, 103.15[ | 10 |
| [103.15, 104.50[ | 7 |
| [104.50, 105.85[ | 7 |
| Total | 30 |
La classe modale est donc [101.80, 103.15[ .
Le mode est estimé à (101.80 + 103.15)/2 = 102.475.
L'effectif total est N = 30 , N/2 = 15. La médiane est donc la moyenne
de la 15e et 16e données qui se trouvent toutes les
deux dans la classe [101.80, 103.15[.
La classe médiane est donc [101.80, 103.15[.
La médiane est estimée au milieu de la classe médiane; c'est à dire: (101.80 + 103.15)/2 = 102.475.
La moyenne est éstimée à:
[5 x (99.10 + 100.45)/2 + 1 x (100.45 + 101.80)/2 + 10 x (101.80 + 103.15)/2 +
7 x (103.15 + 104.50)/2 + 7 x (104.50 + 105.85)/2]/30 = 102.92 g.
4. Histogramme
4.1. Définitions
L’histogramme est la représentation graphique
d’un tableau de données groupées en classes.
Les classes sont placées sur l’axe des abscisses.
Les effectifs sont placés sur l’axe des ordonnées.
Dans un histogramme, on mentionne le titre.
Si la première classe ne commense pas par zéro,
on fait une coupure d’axe (-//-).
4.2. Exemple
Histogramme des masses des 30 mandarines:
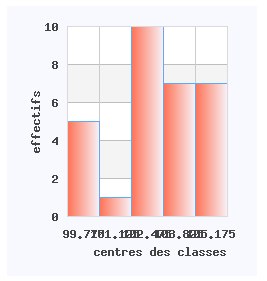
Diagramme circulaire (camembert) :
|
|



