Mathématiques 2: Quick Stats

1. Échatillonnage

On considère quatre méthodes d'échantillonnage

1- L'échantillonnage aléatoire:

On choisi individuellement et de façon aléatoire les individus de l'échantillon. Chaque élément de la population a la même probabilité d'être choisi.

Ceuillir un échatillon de 30 oranges d'un verger d'orangers.

2- L'échantillonnage par grappes:

On subdivise une population homogène en grappes (sous-groupes).

On choisi aléatoirement des grappes et on considére tous les éléments de chacune de ces grappes.

On divise une ville en 21 quartiers (grappes). On choisi aléatoirement 8 quartiers et en interroge tous les habitants de ces 8 quartiers.

3- L'échantillonnage systématique:

On considère tous une population de taille N (compte N individus), puis un échatillon de taille n (n individus).

On fait le rapport r = N/n.

On prend un premier, le deuxième est le r eme de la liste, puis le 2r eme, et ainsi de suite jusqu'à N, toujours en faisant des bonds de r.

4- L'échantillonnage stratifié:

On subdivise une population hétérogène en strates (sous-groupes).

La population compte N = N1 + N2 individus:

N1 individus d'un espèce,
N2 individus d'un autre espèce

Pour un échatillon de taille n, on doit retrouver dans cet échantillon les mêmes proportions pour chacune des strates:

Ainsi dans l'échatillon de taille n, on aura:

(N1/N) x n individus d'un espèce
(N2/N) x n individus d'un autre espèce

2. Sources de biais

Un résultat faux provient des moyens biaisés

Un échatillon de taille trop petite, une mauvaise méthode de calcul, un instrument de mesure imprécis, ou élimination de certains résultats, sont des sources de biais qui faussent la conclusion d'une étude.

2. Mesures de position

Pour une distribution ordonnée , une mesure de position nous renseigne sur la position d'une donnée par rapport aux autres données.

Les mesures de position les plus utilisées sont les quartiles.

Ils séparent la distribution ordonnée en 4 groupes d'effectifs égaux . Ils sont symbolisés par Q1, Q2, Q3.

Q1, Q2, Q3 correspondent à 3 médianes.

Chaque groupe contiendra 25% des données.

• Exemple 1

Voici une distribution ordonnée

2 3 4 7 9 8 11 13 15 15 18

Procédure:

1. Commencer par trouver Q2. n = 11 Impair.
Donc, (n + 1)/2 ==> 12/2 = 6

Q2 se retrouvera à la 6ième position.

Q2 = 8

2. Par la suite, trouver Q1 :

La 6ième position est prise par Q2.

On se concentre sur les 5 premières positions.
n = 5 Impair. Donc, (n+1)/2 ==> 6/2 = 3.
Q1 se retrouvera à la 3ième position.

Q1 = 4

3. Par la suite, trouver Q3 en se concentre sur les 5 dernières positions car la 6ième position est prise par Q2.

La 3ième position à partir de Q2 est 9

Q3 = 15

• Exemple 2

Voici une distribution ordonnée

4 6 9 8 11 13 15 15 18

Procédure:

1. Commencer par trouver Q2. n = 9 Impair.
Donc, (n + 1)/2 ==> 10/2 = 5

Q2 se retrouvera à la 5ième position.

Q2 = 11

2. Par la suite, trouver Q1 :

La 5ième position est prise par Q2.

On se concentre sur les 4 premières positions.
n = 4 pair. Donc, n/2 ==> 2/2 = 2.

On fait la moyenne entre la 2ième et la 3ième donnée.

(6 + 9)/2 = 7,5

Q1 = 7,5

3. Par la suite, trouver Q3 en se concentre sur les 4 dernières positions car la 5ième position est prise par Q2.

n= 4 Pair. Donc, n/2 ==> 4/2 = 2.

On fait la moyenne entre la 2ième et la 3ième données à partir de Q2.
(15+15)/2 = 15
Q3 = 15

3. Données éloignées (aberrantes)

Ces données fausses la représentation réelle de la distribution. Formule :

x < Q1 – 1,5(Q3 - Q1)
x > Q3 + 1,5(Q3 - Q1)

On rejette ces données lors de la construction du diagramme de quartile.

Q1 = 40, Q3 = 60 . Donc

Q3 - Q1 = 20
1,5(Q3 - Q1) = 30

Q1 – 1,5(Q3 - Q1) = 40 - 30 = 10
On rejette toutes les valeurs inférieures à 10.

Q3 + 1,5(Q3 - Q1) = 60 + 30 = 90
On rejette toutes les valeurs supérieures à 90.

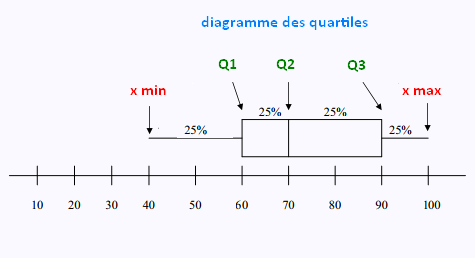
4. Diagramme de quartiles:

Le diagramme de quartiles se compose de deux rectangles et de deux tiges et met en évidence le minimum, le maximum, Q1, Q2, Q3 et les données éloignées.
Il nous renseigne sur la dispersion et la concentration des données.

Exemple 1

Voici une distribution de données :

20 40 60 65 65 75 80 90 95 100

Nous avons:

Nous avons:

Xmin = 20, Q1 = 60 , Q2 = 70 , Q3 = 90 ,> Xmax = 100.

Exemple 2

Voici deux diagrammes de quartiles représentant les résultats de pesées en grammes de deux groupes différents de clémentines.
On selectionne ces agrumes sur leurs masses.


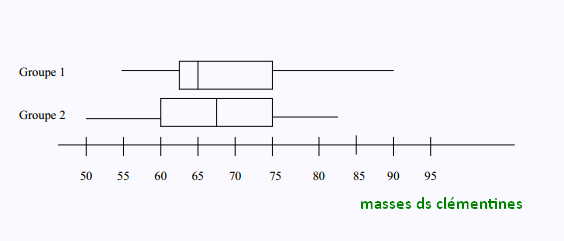
a) Dans quel groupe les masses sont-elles les moins dispersées?
. Groupe 2 car l’étendue est plus petite (32,5 contre 35 pour le groupe 1).

b) Dans quel groupe se trouve la médiane la plus élevée?
. Groupe 2 avec 67,5

c) Dans quel groupe se trouve la clémetine la plus lourde?
. Groupe 1 avec 90.

d) La masse acceptable est de 60 g. Quel est le pourcentage approximatif des clémentines qui sont acceptables dans le groupe 2?
. Le diagramme de quartiles est séparé en 4 parties à peu près égales. Donc, environ 75%.

e) Le pourcentage des masses acceptables est-il plus élevé dans le premier groupe?
. Oui car le premier quartile est à environ 62,5. Donc le pourcentage d'acceptation est supérieur à 75%

f) Le pourcentage des clémentines qui pèsent plus que 75 g est-il plus élevé dans le premier groupe?
. Non car le troisième quartile dans les deux groupes est 75 g. Ainsi, dans les deux groupes, il y a 25% des clémentines qui pèsent plus que 75 g.

Exemple 3

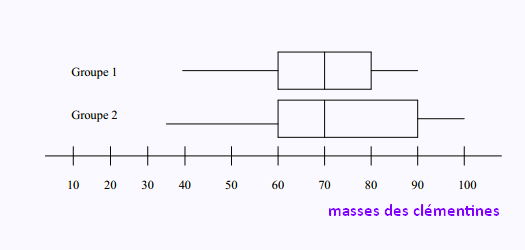
Voici deux diagrammes de quartiles représentant les résultats de pesées en grammes de deux groupes différents de clémentines. .

Questions générales par rapport au diagramme de quartiles ci-dessus

1. Combien de données, en pourcentage, sont inférieures à Q3 dans le groupe 1?
. 75%

2. Dans quel groupe les données sont plus homogènes?
. Dans le groupe 1 car l’étendue est la plus petite (E = 50).

3. Dans quel groupe les données sont plus hétérogènes?
. Dans le groupe 2 car l’étendue est plus grande (E = 65 environ). Ainsi, les données sont plus dispersées donc plus variées.

4. Dans quel groupe y a-t-il le plus de clémentines lourdes?
. Les deux groupes ont 75% des masses acceptables.

5. Dans quel groupe l’étendue interquartile est la plus petite?
. Dans le groupe 1 avec une EI = 20, car pour le groupe 2, nous avons EI= 30.

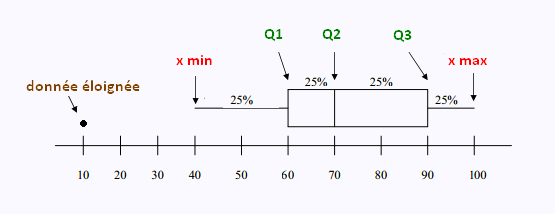
Exemple 4 : données éloignées

Voici une distribution de données :

10 40 60 65 65 75 80 90 95 100

x < Q1 – 1,5(Q3 - Q1) = 60 – 1,5(30) = 15.

Donc toutes les données en bas de 15 ne sont pas incluses dans le diagramme de quartiles.

Ainsi, on ne considère pas le 10.

x > Q3 + 1,5(Q3 - Q1) = 90 + 1,5(30) = 135.

Donc toutes les données en haut de 135 ne sont pas incluses dans le diagramme de quartiles.

Nous avons:

Xmin = 40, Q1 = 60 , Q2 = 70 , Q3 = 90 , Xmax = 100 .