Mathématiques 2: Statistiques : Représentation graphique
Le caractère d'une suite statistique peut être quantitatif,
c'est à dire numérique discret ou continu. Il peut ëtre
aussi quantitatif lorsqu'il n'est pas chiffré. Sa valeur
peut être unique ou prendre plusieurs valeurs sur
une classe.
Une série statistique se présente sous forme d'une
liste de valeurs, de tableau, ou d'une représentation
graphique.
Pour une repésentation graphique, on distingue une représentation
cartésienne, un diagramme en bâtons, un histogramme,
ou un diagramme circulaire.
1. représentation cartésienne: diagramme de points
1.1. Définition
La représentation cartésienne de la valeur d'un caractère est un ensemble de points sur un plan cartésien.
L'abscisse d'un point est le caractère de la série statistique,
et son ordonnée est la valeur de ce caractère. Cette valeur peut être soit l'effectif du caractère, soit son effectif cumulé, sa fréquence ou sa fréquence cumulée.
Cette représentation peut être utilisé lorsque le
caractère statistique étudié est quantitatif,
et la valeur correspondante est quantitative ou
quantitative.
1.2. Exemple

Un boîte contient 80 oranges. On veut peser ces oranges
pour comparer leurs masses. Voici les
résultats obtenus sous forme d'une série statistique:
| masse d'une orange (g) |
190 | 195 | 198 | 200 | 203 | 205 | 210 | 212 |
| son effectif |
7 | 8 | 15 | 20 | 12 | 9 | 6 | 3 |
| effectif cumulé |
7 | 15 | 30 | 50 | 62 | 71 | 77 | 80 |
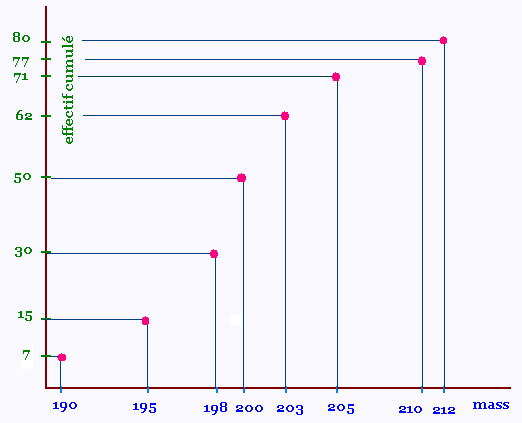
Voici la représentation cartésienne des effectifs
cumulés de cette série statistique:
2. Diagramme en bâtons
2.1. Définition
Lorsque le caractère statistique étudié est
quantitatif et discret (juste des nombres entiers),
on peut représenter la série statistique étudiée par
un diagramme en bâtons
Le point caractère de chaque bâton est représentée horizontalement.
La hauteur de chaque bâton, qui est la valeur asoociée au caractère,
est représentée verticalement.
Cette hauteur du bâton peut être l'effectif ou la fréquence, ou
tout autre grandeur statistique associée au caractère statistique.
Lorsque la variable (caractère) est discrète , on ne joint pas les sommets de bâtons puisque, par définition, il n’existe pas de valeur intermédiaire entre deux variables (caractères).
2.2. Exemple
On reprend l'exemple de la boîte des oranges:
| masse d'une orange (g) |
190 | 195 | 198 | 200 | 203 | 205 | 210 | 212 |
| son effectif |
7 | 8 | 15 | 20 | 12 | 9 | 6 | 3 |
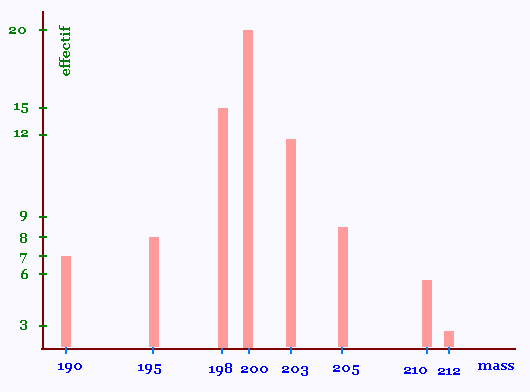
Voici le diagramme en bâtons représentant cette série:
3. Histogramme
3.1. Définition
Lorsque le caractère étudié est quantitatif et continu, on regroupe
les effectifs en classe pour représenter la série par un histogramme.
l’aire de chaque rectangle représente l’effectif (ou à la fréquence)
associé à chaque classe.
Dans un histgramme, l’aire de chaque rectangle est proportionnelle
à l’effectif (ou à la fréquence) associée à chaque classe.
Deux cas sont possibles:
1. l'amplitude des classes est constante:
Lorsque les classes ont la même amplitude, la hauteur de chaque
rectangle qui est proportionnelle à l’effectif.
2. l'amplitude des classes n'est pas constante:
Lorsque les classes n'ont pas la même amplitude, et pour que
l’aire de chaque rectangle reste proportionnelle à l’effectif
(ou à la fréquence) associée à chaque classe, il faut faire
la transformation suivante:
Si la classe de plus grande amplitude est n fois plus grande
que l'amplitude de base, alors on divise l'effectif (ou la fréquence) par n et
on le montre par des un segment en pointillé.
3.2. Exemple
Un boîte contient 80 oranges. On veut peser ces oranges
pour comparer leurs masses. Voici les
résultats obtenus sous forme d'une série statistique:
Ici, le caractère étudié (masse d'une orange) est
quantitatif et continu.
L'amplitude est constante:
| masse (m) d'une orange (g) |
194
≤m<
196 | 196
≤m<
198 | 198
≤m<
200 | 200
≤m<
202 | 202
≤m<
204 | 204
≤m<
206 |
| son effectif |
10 | 8 | 15 | 20 | 15 | 12 |
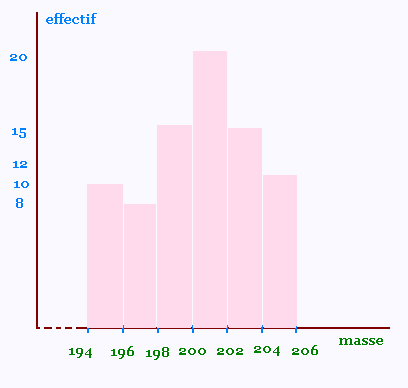
Voici le diagramme en bâtons représentant cette série:
L'amplitude n'est pas constante:
On repète l'expérience de pesage des 80 oranges. Voici les
résultats obtenus sous forme d'une série statistique:
204
| masse (m) d'une orange (g) |
194
≤m<
196 | 196
≤m<
198 | 198
≤m<
200 | 200
≤m<
204 | 204
≤m<
206 |
| son effectif |
10 | 9 | 15 | 34 | 12 |
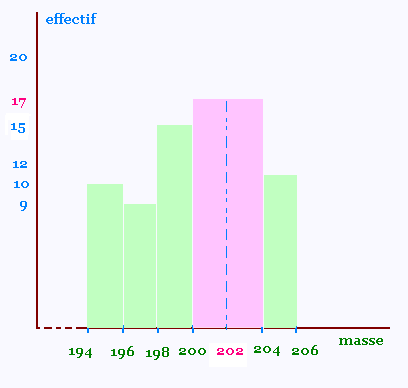
Voici le diagramme en bâtons représentant cette série:
Polygone des effectifs ou des fréquences
Le polygone des effectifs est obtenu en joignant par des segments de droite les milieux des bases supérieures des rectangles .
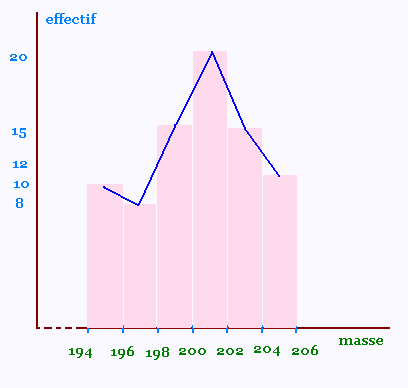
Courbes des effectifs ou des fréquences
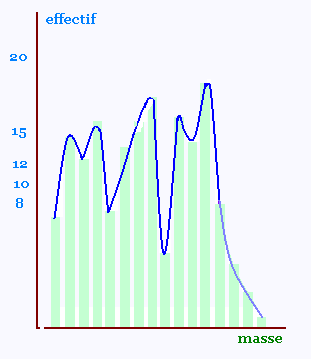
Lorsque les données sont nombreuses et l’intervalle des classes est très petit, la ligne brisée du polygone tend à devenir une courbe appelée courbes des fréquencesou courbes des effectifs .
4. Représentation circulaire
1. Définition
Lorsque le caractère est qualitatif, on représente la série par un diagramme circulaire
la mesure de chaque secteur angulaire represente l’effectif (ou à la fréquence) associé.
2. Exemple
On considère la même contient 80 oranges. On s'interesse
maintenant à la qualité de ces oranges. Voici les
résultats obtenus sous forme d'une série statistique:
| qualité d'une orange |
très bonne | bonne | moyenne | mauvaise | très mauvaise |
| effectif |
35 | 15 | 10 | 15 | 5 |
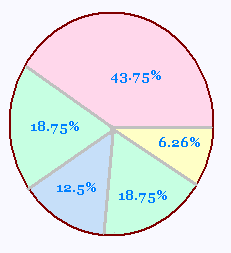
| fréquence (%) |
43.75 | 18.75 | 12.5 | 18.75 | 6.25 |
Voici la représentation circulaire de cette série:
|