Maths
- 2 -
Statistiques
© The scientific sentence. 2010
|
|
Mathématiques 2: Statistiques:
Médianes & quartiles
Exercice n°1 :
Déterminer la valeur médiane des listes de valeurs suivantes :
a) 12,6,18,14,16,9.5,11,8,7.5
b) 14,6.5,11.5,9,12,11,11,9.5
c) 51.2,49.7,54.4,48.5,50.1,49.2,53.8
d) 5.1,7,9.6,13.2,16.6,19.1,4.5,7,5.1
Réponses:
11, 11, 50.1, et 7
Exercice n°2 :
Un client a noté le prix en dollars d'une même
marchandise dans dix points de vente différents :
14.2,13.8,14.2,13.9,14,14.1,13.8,14.3,15.2,13.5
1. Donner un prix médian de cette série.
2. Calculer le prix moyen.
3. Calculer l’étendue de cette série.
Réponses:
14.05 $, 14.1 $, 1.7 $
Exercice n°3 :
Voici, rangées dans l’ordre croissant, les 15 notes
obtenues en mathématiques par Augustin au cours du premier semestre:
4,6,6,9,11,11,12,13,13,13,14,15,17,18,18
1. Quelle est la fréquence de la note 13 ?
2. Quelle est la note moyenne ?
3. Quelle est la note médiane ?
4. Quelle est l’étendue de cette série de notes ?
Réponses:
3/15 = 1/5 = 0.2
180/15 = 12
V(8) = 13
Étendue = 18 - 4 = 14
Exercice n°4 :
Voici le diagramme en bâtons
représentant la répartition des notes
obtenues à un contrôle de mathématiques
par une classe de 3°:
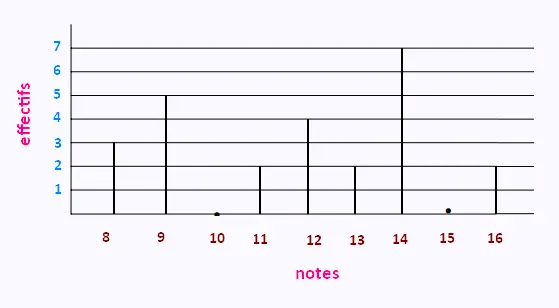
1. Calculer la moyenne de la classe à ce contrôle.
2. Quelle est l’étendue de cette série de notes ?
3. Calculer le pourcentage d’élèves ayant obtenue une note supérieure à 10.
Réponses:
295/25 = 11.8
16 – 8 = 8
(2 + 4 + 2 + 7 + 2)/25 = 0.68.
68 % des élèves ayant obtenue une note supérieure à 10.
Exercice n°6 :
On s'interesse au poids des abricots. Les résultats sont les suivants :
Masse en g: 46,47,48,49,50,51,52,53,54
Effectif: 3,2,6,10,8,5,4,2,1

1. Reproduire et compléter le tableau avec la ligne
des effectifs cumulés croissants.
2. Trouver la médiane de cette série.
3. Calculer l’étendue de cette série.
Réponses:
Effectifs cumulés croissants:
3,5,11,21,29,34,38,40,41
41 impair →(41 -1)/2 = 20 → Me = V(21) = 49
Étendue : 54 – 46 = 8.
Exercice n° 7
1. Déterminer les quartiles Q1 et Q3 de la série statistique suivantes :
2,4,5,6,7,11,13,25,34,43,44,47,51
2. En déduire la valeur de l’écart interquartile.
Réponses:
N = 13 n'est pas multiple de 4 → n = N/4 = 3...
→ Q1 = V(3 + 1) = V(4) = 6
n = 3 N/4 = 9... → Q3 = V(9 + 1) = V(10) = 43
Q3 - Q1 = 43 – 6 = 37.
Exercice n° 8
1. Ordonner la série suivante dans l’ordre croissant :
0.098,1.02,1.1,0.94,1.18,1.23,1.07,1.31,0.8,1.15,0.83
2. Déterminer les quartiles Q1 et Q3 de cette série. puis
l’écart interquartile.
Réponses:
0.098,0.8,0.83,0.94,1.02,1.07,1.1,1.15,1.18,1.23,1.31
N = 11 n'est pas multiple de 4 → N/4 = 11/4 = 2...
→ Q1 = V(3) = 0.83
n = 3 N/4 = 33/4 = 8... → Q3 = V(8 + 1) = V(9) = 1.18
Q3 - Q1 = 1.18 – 0.83 = 0.35.
Exercice n° 9
Antoine a noté, à chaque midi, pendant 12 jours la
température en degré Celsius:
-3,-4,0,1,5,5,2,-1,-5,2,6,7
1. Calculer la moyenne de cette série.
2. a) Ranger cette série statistique dans l’ordre croissant.
b) Déterminer la médiane de cette série.
c) Déterminer les quartiles de cette série.
3. Calculer l'étendue de cette série de données.
Réponses:
m = 15/12 = 1.25oC.
-5,-4,-3,-1,0,1,2,2,5,5,6,7
N = 12 est pair n = N/2 = 12/2 = 6.
→ Me = (V(6) + V(7)/2 = (1 + 2)/2 = 3/2 = 1.5oC
N = 12 est multiple de 4 → N/4 = 12/4 = 3.
→ Q1 = V(3) = - 3
n = 3 N/4 = 36/4 = 9. → Q3 = V(9) = 5oC.
Étendue = 7 – (- 5)= 12oC.
Exercice n° 10
Voici les poids, en carat, de certains diamants ronds-brillants
, ainsi que leurs nombres disponibles respectifs, à vendre par une joaillerie:
Masse (carat): 0.55,0.60,0.65,0.70,0.75,0.80,0.85,0.90
Effectif: 4,14,26,11,7,12,7,5

1. Calculer l’effectif total des diamants.
2. Calculer l’arrondi au centième, en grammes, du poids moyen d’un diamant.
3. Reproduire et compléter le tableau avec la ligne des effectifs cumulés croissants.
4. Déterminer le poids médian d’un diamant.
5. Déterminer les premier et troisième quartiles de cette série.
6. Calculer l’étendue de la série.
1 carat = 0.20 gramme.
Réponses:
L’effectif total est 86.
m = 60.5/86 ≈ 0.70 carat = 0.70 x 0.20 = 0.14 gramme
Effectifs cumulés croissants : 4,18,44,55,62,74,81,86
N = 86 est pair n = N/2 = 86/2 = 43.
→ Me = (V(43) + V(44)/2 = (0.65 + 0.65)/2 = 0.65 carat
N = 86 n'est pas multiple de 4 → N/4 = 86/4 = 21....
→ Q1 = V(21 + 1) = V(22) = 0.65 carat
n = 3 N/4 = 3 x 86/4 = 64...
→ Q3 = V(64 + 1) = V(65) = 0.80 carat
Étendue = 0.90 – 0.55 = 0.35 carat.
|
|