Mathématiques 2: Statistiques:
Médianes & quartiles

Exercice n°1 :

On a relevé les masses en grammes des oranges cueillies d'un verger d'oranges:

203,187,185,206,180,188,198,195,200,195,218,210

1) Quelle est la population étudiée ? Quel est le caractère étudié ?
2) Calculer la moyenne, arrondie au cm prés, de cette série statistique.
3) Déterminer la médiane de cette série.
4) Déterminer le premier et le troisième quartile de cette série
5) Interpréter les résultats.

Réponses:

1) La population étudiée est les oranges cueillies d'un verger.
Le caractère c'est la masse des oranges.

2) la moyenne de la série : (203 + 187 + 185 + 206 + 180 + 188 + 198 + 195 + 200 + 195 + 218 + 210)/12 = 197 grammes.

3) la médiane
D'abord ranger la série statistique dans l'ordre croissant :

180,185,187,188,195,195,198,200,203,206,210,218

Il y a 12 valeurs, N = 12 : pair n = N/2 = 12/2 = 6
→ Me = (V(6) + V(7))/2 = (195 + 198)/2 = 196.5 grammes

4) 1er quartile : N = 12 est multiple de 4 , n = N/4 = 3
→ Q1 = V(n) = V(3) = 187 grammes.

3ème quartile : n = 3N/4 = 3 x 12/4 = 9
→ Q3 = V(n) = V(9) = 203 grammes.

5) Interprétation

. Dans cet échantillon d'oranges, une orange pèse en moyenne 196.5 grammes.
. la moitie de ces agrumes ont une masse ≤ 196.5 grammes.
. au moins 1/4 = 25% de ces oranges a une masse ≤ 187 grammes.
. au moins 3/4 = 75% de ces oranges a une une masse ≤ 203 grammes.
. au moins 1/4 = 25 % de ces oranges a une masse ≥ 203 grammes.

Exercice n°2 :

Voici les notes obtenues par 13 élèves à un devoir de Sciences Physiques :

6,8,8,9,9,10,11,12,14,17,18,18,19

1) Calculer la moyenne, arrondie au centième, de cette série de notes.
2) Déterminer la médiane de cette série de notes.
3) Déterminer le premier quartile de cette série de notes.
4) Déterminer le troisième quartile de cette série de notes.

Exercice n°3 :

Voici une série statistique :

25,12,13,20,17,9,1,15,8,23,14,17

Pour cette série déterminer :

1) La médiane
2) Le premier quartile
3) Le troisième quartile.

Exercice n°4:

Voici une série statistique :

10,25,12,13,20,17,9,1,15,8,23,14,17

Pour cette série déterminer :

1) La médiane
2) Le premier quartile
3) Le troisième quartile.

Exercice n°5:

Le tableau ci-contre donne la répartition des notes obtenues à un contrôle de mathématiques par les 27 élèves d’une classe de 3e:

Note	6	8	10	13	14	17
Effectif	3	5	6	7	5	1

1) Calculer la note moyenne de la classe à ce contrôle.
Arrondir le résultat à l’unité.
2) Calculer la pourcentage d’élèves ayant eu une note supérieure ou égale à 10.
Arrondir le résultat au dixième.
3) Déterminer la médiane de cette série.

Exercice n°6:

Voici une série croissante de valeurs avec ses effectifs respectifs:

Valeur	6	7.5	8	8.5	9	x
Effectif	1	2	4	3	1	y

1) Déterminer y pour que la médiane de cette série soit égale à 8.
2) Si y = 4, calculer x pour que la moyenne de la série soit égale à 8.

Exercice n°7:

Le tableau ci-dessous présente la série des notes obtenues par les élèves de 3e lors d'un devoir à la maison:

Note/20	20	5	6	8	9	11	12	13	15	18	19
Effectif	1	2	6	2	1	4	2	3	1	1

1) Quel est l’effectif de cette classe ?
2) Calculer la note moyenne de ce devoir.
En donner la valeur arrondie au dixième de point.
3) Quel pourcentage, arrondi à l’unité, de l’effectif total représentent les élèves ayant obtenu une note inférieure ou égale à 8 ?
4) Déterminer la note médiane de cette série. Que représente-t-elle ?

Exercice n°8:

Voici le diagramme en bâtons des notes obtenues par une classe de 3e de 25 élèves au dernier rapports de laboratoires en Chimie:



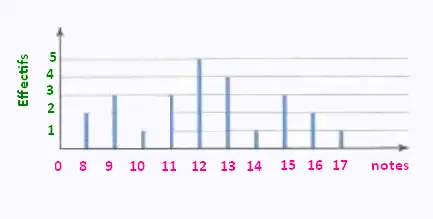
1) Calculer la moyenne des notes.
2) Déterminer la médiane des notes.
3) Calculer le pourcentage des élèves ayant obtenu une note strictement supérieur à 13.
4) Déterminer le premier quartile de cette série de notes.
5) Déterminer le troisième quartile de cette série de notes.

Exercice n°9:

Lors d'un contrôle en Mathématiques, un groupe d’élèves de 3e a obtenu les notes suivantes:

6,7,7,8,9,9,9,10,12,12,13,14,15

1) Quelle est l’étendue des notes ?
2) Quelle est la moyenne des notes ? Arrondir au dixième de point
3) Quelle est la note médiane ?
4) Déterminer le premier quartile de cette série de notes.
5) Déterminer le troisième quartile de cette série de notes

Exercice n°10:

Au cours d’une course d’athlétisme de 400 m, le temps mis par chaque coureur a été chronométré. Voici le temps de chacun des athlètes (en s) :

48.65,49.20,50,50.12,50.13,50.45,51,51.80,51.85, 51.90,52.05,52.20,52.60,53.28,54.80

1) Quelle est l’étendue de cette série ?
2) Déterminer la moyenne arrondie au centième de cette série.
3) Donner la médiane de cette série.
4) Quel pourcentage de coureurs ont mis moins de 52,50 secondes pour effectuer les 400 mètres ?

Exercice n°11:

Voici la série des tailles en centimètres des élèves d'une classe de secondaire 4:

165,175,187,165,170,181,174,184,171,166,178,177,176,174,176

1) Calculer la taille moyenne de ces élèves.
2) Quelle est la taille médiane de ces élèves. Justifier.
3) Quelle est l’étendue de cette série ?

Exercice n°12:

Une auto-école possède 12 voitures. Les consommations moyennes, en litre d’essence, de chaque véhicule pour 100 km sont les suivantes:

16.7,7.8,8.2,10.1,9.3,6.9,7.7,6.8,8.5,9,10.2,11


1) Calculer la consommation moyenne aux 10 km des ces voitures.
2) Déterminer la médiane de cette série.
3) Déterminer le premier et le troisième quartiles de cette série.
4) Sans refaire de nouveaux calculs, dire si l’affirmation suivante est exacte :
« 50% des voitures de cette auto-école consomme entre 7 L et 9 L aux 100 km ».

Exercice n°13:

Voici les douzes températures moyennes relevées mensuellement, de janvier à décembre, en une année dans deux villes A et B.

Ville A: 5,7,8,10,14,18,22,23,16,12,9,6
Ville B: 12,13,11,14,12,13.5,11.5,13,10,12,14,14

1) Calculer la moyenne de chaque série de températures.
2) Déterminer la médiane de chaque série.
3) Calculer l’étendue de chaque série.
4) Déterminer le premier et le troisième quartile de chaque série.
5) Comparer ces deux séries de températures.

Exercice n°14:

Vérifier les affirmations suivantes pour cette série:

4.5,10.5,16,2.5,10,12,2.5,4.4,5,7.5,7.5,10.

1) L’étendue est de 16.
2) La moyenne est 7.
3) La médiane est 7,5.
4) Le premier quartile est 4,5.
5) Le troisième quartile est 10,5.

Exercice n°15:

La famille Oersted a noté sa consommation mensuelle de lait, en une année, de janvier à décembre. Elle obtient:

Volume (en l): 40,25,20,15,24,30,32,28,36,24,35,51



1) Calculer le volume de lait moyen consommé par mois.
2) Déterminer le volume médian.
3) Déterminer le premier et le troisième quartiles.
4) L’affirmation suivante est-elle exacte ?:
« 50% des volumes mensuels de lait consommées est compris entre 24 l et 39 l »

Exercice n°16:

Une usine teste des ampoules électriques, sur un échantillon, en étudiant leur durée de vie en heures. Voici les résultats:

d : durée de vie en heures	Nombre d’ampoules
1 000 < d < 1 200	550
1 200 < d <1 400	1 460
1 400 < d < 1 600	1 920
1 600 < d <1 800	1 640
1800 < d < 2 000	430

1) Quel est le pourcentage d’ampoules qui ont une durée de vie de moins de 1 400 h ?
2) Calculer la durée de vie moyenne d’une ampoule.

Exercice n°17:

Un groupe de 15 personnes ont participé à un semi-marathon (une course à pied de 21 km en ville).

Le diagramme en bâtons ci-dessous précise les résultats du groupe:



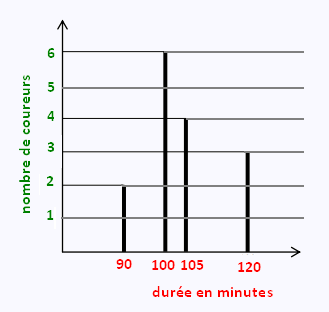
1) Compléter le tableau suivant:

Durée en min	90	100	105	12
Effectif

2) Pour cette série, calculer:

a. l' étendue.
b. la médiane.
c. la moyenne.

Les 9 premiers kilomètres sont en montée, les 12 autres sont en descente. Édouard a parcouru : les 9 premiers kilomètres en 40 minutes, puis les 12 derniers kilomètres en 50 minutes. Calculer sa vitesse moyenne en km/h:

a) en montée.
b) en descente.
c) sur le parcours total.

Exercice n°18:

Les dépenses mensuelles moyennes de James sont était de 2000 $ et ses dépenses mensuelles médianes sont de 1800 $.

Interpréter chacune de ces données.

Exercice n°19:

On considère une série de notes obtenues par des élèves lors d’un examen en Chimie.

Pour cette série, on donne :

1er quartile Q1 = 7,
la médiane Me = 9, et
le 3e quartile Q3 = 15

Pour chaque affirmation, préciser si elle est vraie ou fausse :

1) 1/3 des élèves de la classe ont une note inférieure ou égale à 7.
2) Au moins 25 % des élèves de la classe ont une note inférieure ou égale à 7 .
3) Environ 1/4 de la classe ont eu une note comprise entre 7 et 9 .
4) Moins d’un élève sur quatre a eu plus de 15.
5) Exactement un élève sur deux a eu plus de 9 .
6) Tous les élèves ont obtenu une note comprise entre 7 et 15.

Exercice n°20:

Lors d'une pesée d'abricots, on a relevé la masse (en grammes) de chacun d’eux.

Masse (en g): 35,36,37,38,39,40
Effectif: 4,8,10,14,8,6

1) Calculer la masse moyenne de cette série.
2) a) recopier et compléter le tableau suivant :

Masse m (en g)	Effectif
m ≤ 35
m ≤ 36
m ≤ 37
m ≤ 38
m ≤ 39
m ≤ 40

b) En déduire la médiane de cette série.
3) Interpréter les résultats obtenus précédemment.

Exercice n°21:

On a demandé à des élèves le nombre de livres qu’ils ont lu cette année. Les résultats obtenus sont traduits dans le diagramme en bâton suivant:



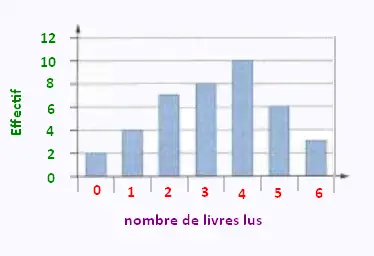
1) Calculer la médiane de la série.
2) Construire un tableau de valeurs et d'effectifs.
3) En déduire la médiane et les quartiles de la série.
4) Interpréter les résultats obtenus.

Exercice n°22:

Au cours d'un laboratoire de Chimie, les élèves d’une classe de 3e ont mesuré, par groupe, le pH de l’eau à l’aide d’un pH-mètre. Voici les résultats obtenus :

6.99,6.9,7.05,6.89,6.94,7.2,7.19,7.08,7.22,6.99,6.99,7.01,7.02

a) Quelle est la population étudiée ? Le caractère étudié ?
b) Quel est le nombre de valeurs ?
c) Quel est le nombre de données ?
d) En déduire l’effectif total.
e) Calculer le pH moyen mesuré.
f) Donner un encadrement au centième de la valeur moyenne du pH.
Le pH-mètre indique la précision de ± 0.01.

Exercice n°23:

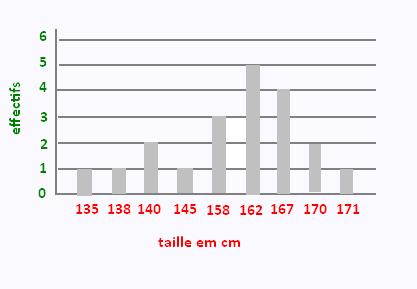
On a mesuré la taille en centimètre d’un groupe de 20 personnes.

a) Quelle est la population étudiée ?
b) Quel est le caractère étudié ?
c) Quelles sont les valeurs prises par le caractère ?
d) Calculer la taille moyenne d’une personne de ce groupe.
e) Déterminer la taille médiane de ce groupe.

Exercice n°24:

Une épreuve de course d'endurance de 5 000 mètres est disputée par douze athlètes.

On considère la série statistique constituée du nombre de kilomètres parcourus par chaque participant.

Un athlète n'a pas participé à la course. Un autre athlète a parcouru tous les 5 000 mètres.

On donne les informations suivantes :

1er quartile = 1000 mètres
Médiane = 3 000 mètres
3e quartile = 4 000 mètres

1) Calculer l’étendue de cette série.
2) Interpréter chaque nombre du tableau

Exercice n°25:

On a relevé, pour 30 familles, le nombre d’enfants par famille :

5,0,3,1,2,7,1,2,3,1,0,1,3,4,0,0,1,1,2,2,1,2,0,1,2,3,0,4,1,4

1) Construire le tableau des effectifs.
2) Représenter cette série statistique par un diagramme en bâtons.
3) Calculer le nombre moyen d’enfants par famille.
4) Déterminer le nombre médian d’enfants par famille.
5) a) Combien de famille ont au plus 3 enfants ?
b) Combien de famille ont au moins 3 enfants ?

Exercice n°26:

Le tableau suivant donne le nombre de barres de mémoires RAM vendues, sur une période d’une semaine, dans un magasin informatique en fonction de leur capacité (en GB).

Capacité: 4,6,8,16
Effectif: 30,50,60,15

1) Calculer la moyenne de cette série. Arrondir au dixième.
2) Déterminer la médiane de cette série.
3) a) Recopier et compléter le tableau suivant :

Capacité (en GB)	4	6	8	16	Total
Effectif	30	40	60	20
Angle (en °)					360

b) Construire un diagramme circulaire représentant ces données.
4) Interpréter les résultats des questions précédentes.

Exercice n°27:

On a relevé quotidiennement, à midi, les températures au centre ville, pendant une semaine du mois d'avril

Jours	L	M	M	J	V	S	D
Température en °C	10	10	2.5	0	3	5	10

Voici le diagramme radar aussi appelé graphique en toile d'araignée :




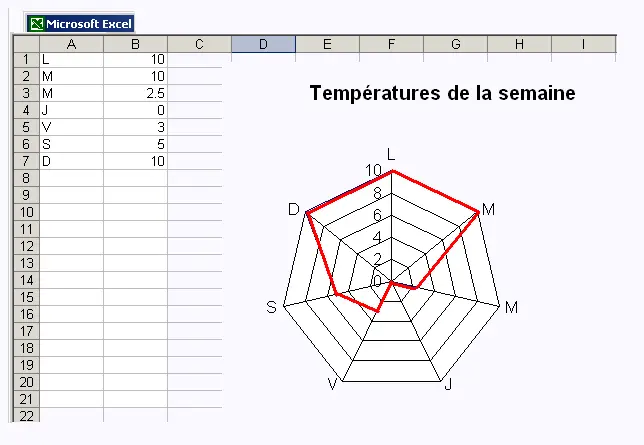
Interpréter ce diagramme.

Exercice n°28:

Lire les définitions suivantes et donner d'autres exemples parmi ceux qui sont écrits:

Le graphique radar est idéal pour représenter, en deux dimensions, les modalités des variables qualitatives en fonction d'une variable discrète qui correspond à un rayon de la toile.

Les variables (ou caractères) sont de deux natures: qualitatives ou quantitatives.

• 1. les variables qualitatives ou variables catégorielles peuvent prendre plusieurs modalités (ou catégories ou niveaux).

Exemple: Couleur, langue parlée, sexe, jour de la semaine, profession, ...

Les modalités de la variable qualitative couleur: sont: vert, jaune, rouge, violet, bleu, magenta, blanc, ...

• 2. les variables quantitatives ou variables métriques sont mesurées par un nombre.

Exemple : âge, solde bancaire, notes, température, poids, taille ...

Une variable quantitative peut être :

- discrète : elle prend des valeurs isolées entières positives. Ex : nombre d'enfants.
- continue : en théorie , elle peut prendre n'importe qu'elle valeur dans un intervalle.