Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques statistiques
Échantillonnage
Théorème de la limite centrale
Estimation

1. Exemple

Un oranger contient N = 44 oranges. on a cueilli une boîte
comme échantillon qui contient n = 12 oranges. On va faire des
statistiques sur l'échantillon et inférer les résultats
à la population générale qui est l'ensembles des oranges
de l'oranger.
L'individu est une orange. On pèse chaque orange
de la boîte. La variable aléatoire X est la fontion de peser.
Elle a pour valeur une masse d'une orange en grammes.
Plus explicitement:
Peser (orange) = masse d'une
valeur déterminée,
ou
X(individu i) = caractère i avec valeur déterminée xi.
On obtient une série statistique {xi}. Les valeurs
de cette série sont les valeurs images prises par une
variable. Cette variable est variable aléatoire X.
Les xi sont les valeurs de la variable
aléatoire X.
Maintenant on calcule la moyenne des xi,
leur variance et leur écart-type.
Moyenne m = Σxi/n
Variance = s2 = Σ(xi - m)2/n
m et s2 sont respectivement la moyenne et la variance
de l'echantillon.
Cette moyenne m et cette variance s2 sont-elles
la moyenne et la variance de la population?
Les paramètres de la population comme sa moyenne, sa variance,
ou son écart-type sont estimés à partir de ceux de
l'échantillon observé.

L'échantillon tiré de la population, observé donne m pour la
moyenne et s2 pour la variance. Cet échantillon n'est
pas le seul possible. Sans ordre, Il en existe C(N,n) = N!/n!(N - p)!
cas possibles sans remise ou D(N,n) = (N + n - 1)!/n!(N - 1)! cas possibles
avec remise.
Ainsi nous avons C(N,n) ou D(N,n) valeurs possibles pour m et pour
s2. Donc Les valeurs de la moyenne et de
la variance varient selon l'échantillon tiré et observé.
Les C(N,n) ou D(N,n) variables aléatoires X possédent chacune une
espérance, une variance et un écart type.
Soit l'ensemble des xi = {xi} ou la série
statistique {xi} les caractères ou les données de
l'expérience aléatoire i. A cette série i correspond une variable
ou une fonction aléatoire Xi qui produit une moyenne
mi, moyenne pour chaque échantillon i, ou une
variance pour chaque échatillon i.
Xi{xj} = mi = Σxj/n, ou
Vi = Σ(xj - mi)2/n.
n est le nombre de caractères xj, c'est à dire la taille
de l'échantillon i.
L'indice j varie de 1 à n et Σj = n.
Ces valeurs sont attribuées à l'échantillon.
Pour N réalisations indépendantes de la variable aléatoire X,
c'est à dire le nombre d'échatillons pris de la population.
mi étant le résultat de Xi, on ecrit:
mi = Xi. Donc
Moyenne(mi ) = Moyenne(Xi ) =
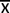 = Σ Xi/N .
D'où: = Σ Xi/N .
D'où:
V = ΣVi/N =
Σ (Xi -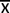 )2/N )2/N
Ces valeurs sont attribuées à la population.
Pour un échantillon de taille N:
 = Σ Xi/N = Σ Xi/N
V = Σ (Xi - )2/N )2/N
2. Estimation
La moyenne ν et la variance σ2 s'ecrivent :
σ2 = Σ(mi - μ)2/N
 = μ = Σ Xi/N = μ = Σ Xi/N
σ2 = Σ(Xi - μ)2/N
Nous avons donc:
s2 = Vi =
Σ(xj - mi)2/n =
Σ(Xj - mi)2/n =
ΣXj2/n - 2 miΣXj/n + mi2 =
ΣXj2/n - 2 miΣXj/n +
mi2 =
ΣXj2/n - 2 mi2 + mi2 =
ΣXj2/n - mi2 =
On estime la moyenne μ de la population
égale à la moyenne m de l'échantillon:
m = μ
On estime la variance σ2 de la population
égale à la variance s2 de l'échantillon corrigée
par le facteur k(N,n):
σ2 = k(N,n) s2
k(N,n) = (N - 1)/N x n/(n - 1) dans le cas du tirage sans remise , et
k(N,n) = n/(n - 1) dans le cas du tirage avec remise
On remarque que, lorsque N est grand, (N - 1)/N vaut 1, et donc
le facteur k(N,n) est le même et vaut n/(n - 1) que ce soit
sans remise ou avec remise.
On considère généralement, le cas simple, sans remise,
c'est à dire celui des combinaisons C(N,n).
σ2 = n/(n - 1) . s2
L'estimateur d'une variable aléatoire est égale
à sa valeur estimée.
1. L'estimateur de la variable aléatoire
"moyenne" X s'ecrit ℰ(m) = Moyenne(X). Il est
défini par:
ℰ(m) = μ , avec m = Σxi/n. m est
la moyenne de l'échantillon, appelée moyenne empirique de X;
et μ est la moyenne inférée à la population.
On dit que l'estimateur moyenne est sans biais
puisqu la moyenne de l'échatillon m est estimé égale
à la moyenne de μ de la population.
2. L'estimateur de la variable aléatoire
"variance" Y s'ecrit ℰ(s2) = Variance(Y). Il
est défini par:
ℰ(s2) = σ2 = n/(n - 1)s2 ,
avec s2 = Σ(xi - m)2/n. s2
est la variance de l'échantillon, appelée variance empirique de Y;
et σ2 est la variance inférée à la population.
On dit que l'estimateur variance est biaisé
puisqu la variance de l'échatillon s2 est estimé différente
de la variance σ2 de la population.
|
|