Statistiques
Statistiques
descriptives
Échantillonage
Éstimation
Statistiques
inférentielles
Statistiques
Calculateurs
© The scientific sentence. 2010
|
Mathématiques 2: Statistiques
Espérance mathématique
Dés de la chance
Espérance mathématique : dés de la chance

On lance deux dés à la fois. Le montant gagné correspond à
la somme des nombres des deux faces obtenues. Combien espère -t-on gagner?
Réponse:
C'est le résultat de l'espérance mathéatique.
L'espérance (mathématique) d'une variable aléatoire numérique X est la valeur
que l'on peut espérer obtenir, en moyenne, en réalisant X. On la note E(X).
• dans le cas d'une variable X discrète, de loi de probabilité
définie par les xi et les pi, l'espérance de X est la moyenne des xi, pondérée par les pi.
E(X) = Σ(xipi)
• dans le cas d'une variable X continue, de fonction de densité f,
l'espérance de X est l'intégrale, sur l'intervalle des valeurs de X,
de la fonction xf(x) :
E(X) = ∫ xf(x)dx
On lance deux dés cubiques et on note la somme des faces
obtenues.
La variable aléatoire X = somme des numéros des faces obtenues. Cette
variable prend les valeurs de 0 à 12 . Sa loi de probabilité
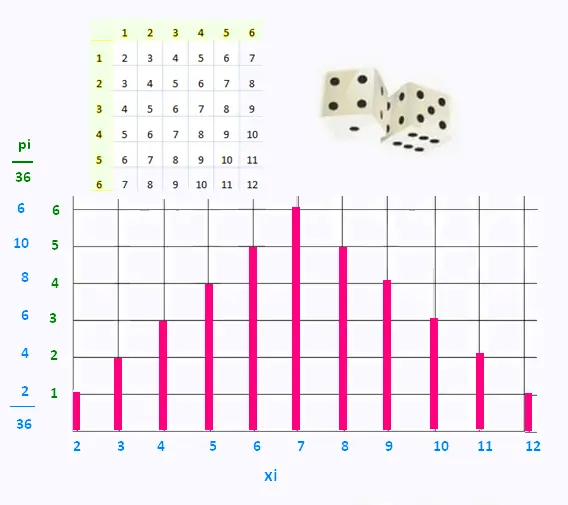
définie par les xi et les pi est définie dans le tableau suivant:
| xi | 2 | 3 | 4 |
5 | 6 | 7 | 8 |
9 | 10 | 11 | 12 |
| pi (/36) | 1 | 2 | 3 |
4 | 5 | 6 | 5 |
4 | 3 | 2 | 1 |
E(x) = (1/36) [(2 x 1) + (3 x 2) + (4 x 3) + (5 x 4) + (6 x 5) + (7 x 6)
+ (8 x 5) + (9 x 4) + (10 x 3) + (11 x 2) + (12 x 1)] =
(2 + 6 + 12 + 20 + 30 + 42 + 40 + 36 + 30 + 22 + 12)/36 =
252/36 = 7
L'espérance de gain à ce jeu de dés est la moyenne des gains possibles,
pondérée par les probabilités.
Si un point sur la face du dé est équivalent à 10.00$, alors
l'espérance de gain est 70$.
|
|