Mathématiques 2: Statistiques:
          Quartiles &
diagramme de quartiles

1. Définition

Les quartiles nous renseignent sur la position d'une donnée par rapport aux autres données d'une distribution ordonnée.

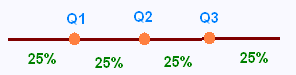
On sépare une distribution de données en 4 sous-ensembles appelés des quarts. Les trois points séparateurs Q1,Q2, et Q3 sont appelés des quartiles.

Chaque quart contient le même nombre de données, donc 25 % des données.

Le deuxième quartile Q2 est la médiane principale Md de la distribution.

Le premier quartile Q1 est la médiane de la distribution de gauche qui reste avant la médiane Q2 = Md.

Le troisième quartile Q3 est la médiane de la distribution de droite qui reste après la médiane Q2 = Md.

Les données éloignées appelées aberrantes donnent une représentation fausse de la réalité de la distribution. Elles sont tout simplement rejetées pendant la construction du diagramme de quartiles.

Une donnée x est rejetée si:

x < Q1 – 1,5(Q3 - Q1)
x > Q3 + 1,5(Q3 - Q1)

2. Exemples

Exemple 1: taille impaire

On considère la série statistique suivante de taille égale à 15:

55, 20, 60, 140, 30, 88, 90, 10, 110, 150, 40, 70, 100, 120, 130.

On range cette série et on obtient:

10, 20, 30, 40, 55, 60, 70, 88, 90, 100, 110, 120, 130, 140, 150.

La taille N = 15 est impaire. C'est donc au (15 + 1)/2 = 8 eme rang que se trouve la médiane principale qui est 88.

La série de gauche entre le minimum et la médiane principale: 10, 20, 30, 40, 55, 60, 70 est de taille impaire égale 7. C'est donc au (7 + 1)/2 = 4 eme rang que se trouve le premier quartile Q1 qui est 40.

Il reste la série de droite entre la médiane principale et le maximum: 90, 100, 110, 120, 130, 140, 150 de taille impaire égale 7. C'est donc au (7 + 1)/2 = 4 eme rang de cette série tronquée que se trouve le troisième quartile Q3 qui est 120.

Ainsi

Q1 = 40
Q2 = Md = 88
Q3 = 120

Exemple 2: taille paire

On considère la série statistique suivante de taille égale à 14:

55, 20, 60, 140, 30, 88, 90, 110, 150, 40, 70, 100, 120, 130.

On range cette série et on obtient:

20, 30, 40, 55, 60, 70, 88, 90, 100, 110, 120, 130, 140, 150.

La taille N = 14 est paire. C'est donc entre 14/2 = 7 eme rang et 14/2 + 1 = 8 eme rang que se trouve la médiane principale qui est (88 + 90)/2 = 89.

La série de gauche entre le minimum et la médiane principale: 20, 30, 40, 55, 60, 70, 88 est de taille impaire égale 7. C'est donc au (7 + 1)/2 = 4 eme rang que se trouve le premier quartile Q1 qui est 55.

Il reste la série de droite entre la médiane principale et le maximum: 90, 100, 110, 120, 130, 140, 150 de taille impaire égale 7. C'est donc au (7 + 1)/2 = 4 eme rang de cette série tronquée que se trouve le troisième quartile Q3 qui est 120.

Ainsi

Q1 = 55
Q2 = Md = 89
Q3 = 120

3. Diagramme de quartiles: boîte à moustaches

3.1. Définitions

Le diagramme de quartiles ext composé d'un rectangle et des moustaches.

Le diagramme de quartiles aide à comprendre la dispersion ou la concentration des données , ou à comparer des distributions de données différentes.


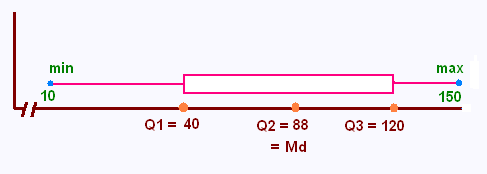
      N = 15 Min = 10 Max = 150
      Q1 = 40 Q2 = Md = 88 Q3 = 120

Les 3 quartiles divisent la distribution de données en 4 quarts contenant le même nombre de données.

Ce rectangle représente l’étendue interquartile = Q3 - Q1 = 120 - 40 = 80.

La lecture du diagramme ne permet pas de déterminer:
- le nombre de données de la distribution, et
- la moyenne de la distribution.

3.2. Exemple

On pèse deux variétés d'abricots Type 1 et Type 2.

Voici les deux diagrammes de quartiles représentant les masses des deux types d'abricots:



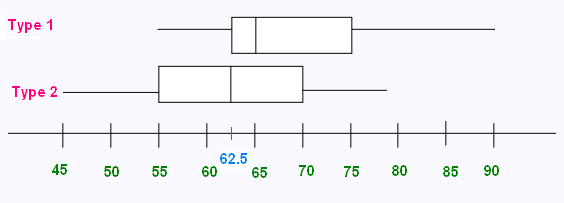
a) Les masses sont moins dispérsées pour le type 1 que pour le type 2, car la dispersion pour le type 1 est de 75 - 62.5 = 12.5 et de 75 - 55 = 15 pour le type 2.

b) La médiane la plus élevée se trouve dans le type 1 avec Md = Q2 = 65.

c) C'est dans le type 1 que se trouve l'abricot

d) On sélectionne les abricots qui pèsent plus que 62.5 grammes. Le pourcentage des abricots à considérer est de 100% pour le type 1 et 50% pour le type 2.

e) Le pourcentage des abricots qui pèsent au moins 75 g est de 25% pour le type 1 et moins que 25% pour le type 2.

f) Il ya 25% d'abricots qui pèsent au plus 62.5 g pour le type 1 et 50% pour le type 2.

4. Exercices

1. Calculer les quartiles des séries suivantes:

a) 10, 16, 18, 14, 16, 11, 11, 9, 15, 19,20
b) 14, 6,5, 11.5, 9, 12, 11, 11, 9,5
c) 50, 22, 40, 57.4, 44.5, 66.1
d) 16, 5.39, 6, 13.2, 6.5, 19.1, 4.5

2. Calculer les quartiles des séries suivantes: et représenter les diagrammes des quartiles correspondants

a) 1,2,3,4,5,6,7,8,9
b) 10,20,30,40,55,66,77,88,99,111
c) 60,62,64,66,68,70,72,74,76,78,80

3. Pour les distributions de données éloignées suivantes, détérminer les données à ne pas considérer au diagramme des quartiles:

a) 10,12,84,15,66,14,12,5, 11.25, 13,3, 2,11.
b)152,150,134,244,859,152,151, 2, 149, 11.
c) 66, 67, 2, 68, 877, 3, 68, 69,70 .

4.Comparer les diagrammes de quartiles suivants relatifs aux masses en grammes de deux types de prunes:





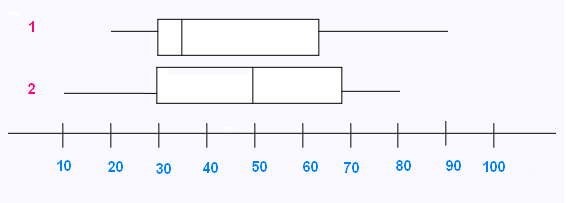
a) On sélectionne les prunes de 50 g et plus. Dans quel groupe se trouvent-elles le plus ?

b)Combien de prunes, en pourcentage, sont supérieures à Q1 ?

c) Dans quel groupe les données sont plus hétérogènes ?

d) Dans quel groupe les données sont plus homogènes ?

e) Dans quel groupe l’étendue interquartile est la plus grande ?